
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные свойства логических операцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1 Ассоциативность: Х1 Ù (Х2 Ù Х3) = (Х1 Ù Х2) Ù Х3 (Х1 Ú Х2) Ú Х3 = Х1 Ú (Х2 Ú Х3) 2 Коммутативность Х1 Ú Х2 = Х2 Ú Х1 3 Двойное отрицание `Х = Х 4Закон противоречия ` Х Ù Х = 0 5Свойства констант Х Ù 1 = Х, Х Ù 0 = 0, Х Ú 1 = 1, Х Ú 0 = Х, 6 Закон «исключения третьего» `Х Ú Х = 1. Эти равенства остаются справедливыми при подстановке вместо переменных любых логических функций. Выражение из букв, знаков операций и скобок, обозначающих высказывание или форму для высказывания, называется формулой алгебрывысказывания. Скобки, как и в обычной алгебре, играют роль знаков препинания и используются для определения порядка операций. Для описания внешнего мира и поиска решений в искусственном интеллекте широко используются язык и аппарат исчисления предикатов. Исчисление (или алгебра) предикатов представляет собой развитие исчисления высказываний и включает его полностью как составную часть. Поэтому знакомство с исчислением предикатов начнем с рассмотрения исчисления высказываний. Исчисление высказываний. В математической логике высказыванием называется такое предложение, которое истинно или ложно. Условимся высказывания обозначать прописными латинскими буквами без индексов и с индексами А, В, С,… и называть пропозициональными. В соответствии с тем, что высказывания могут быть, истинными и ложными, пропозициональные буквы могут принимать истинностные значения - И (истина) и Л (ложь). Иногда, в частности в теории конечных автоматов, вместо истинностных значений (И и Л) используют соответственно 1 и 0. Предикат Р(х), определенный на предметной области М, задает определенное свойство элементам множества М и интерпретируется как обозначение высказывания «х обладает свойством Р», причем Р(х) принимает значение И, если это высказывание истинно, и значение Л, если оно ложно, т.е.предикат трактуется как логическая функция одной или нескольких предметных переменных (одного или нескольких субъектов) в зависимости от того, отражает высказывание свойства предметов или отношения между предметами. Предикат символически обозначают функциональными знаками с одним или несколькими пустыми местами одной или несколькими переменными, занимающими пустые места.
Одноместный предикат обозначается Р() или Р(Х), где X -переменная для чисел или объектов. Область определения этой логической функции - это множество N - натуральных чисел. N ® {И, Л} Р(X) разбивает область определения на два множества: одно истинно, а другое ложно. С помощью многоместных предикатов выражаются отношения между предметами. Двухместный предикат или логическая функция двух числовых переменных Х,У, образующаяся при любой подстановке вместо Х и У пары чисел из области определения D, переводит эту функцию в истинное или ложное высказывание. Предикат Ð (X, У) определен на множестве всевозможных пар чисел из области D, т.е. область определения это множество D (пара чисел), а заполнения - истинно или ложно. D {И, Л} Пусть предикат Ð(х,у) А А ={3, 4, 5, 6} М [(х,у) ÎА L Ð (х,у)] = {(3, 4) (3, 5) (3, 6) (4, 5) (4, 6) (5, 6)} Остальные высказывания ложные. Т.к. предикаты - логические функции, то к ним применимы все операции логики высказываний, позволяющие формировать сложные предикаты. Из предикатов можно (формировать) строить не только высказывания, относящиеся к определенному предмету или определенной системе предметов, но и высказывания выражающие свойства целого множества, т.е. высказывания о всеобщности. Для построения таких высказываний вводится операция называющаяся - квантор. "X - для всех X - квантор общности. Существует Х такое, что - $X - квантор существования. Итак, в логических моделях систему знаний о предметной области, необходимую для решения прикладных задач, рассматривают как совокупность фактов (утверждений). Последовательность действий при формировании вывода достаточно сложна и, безусловно, требует использования вычислительной техники. Вместе с тем исчисление предикатов находит ограниченное применение при создании систем автоматизированного проектирования технологических процессов. В частности, оно используется при создании САПР ТП для выбора схем установок заготовок. ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ: 1. Какие значения принимает логическая функция? 2. Перечислите основные свойства логических операций. 3. Что называется формулой алгебры высказывания? 4. Что можно представить с помощью многоместных предикатов?
Исчисление предикатов
Для примера рассмотрим логические модели процессов проектирования технологии механической обработки деталей резанием. Для построения логической модели процесса проектирования технологии механической обработке рассмотрим два основных множества этого процесса: множество С средств обработки и множество А поверхностей детали. Параметрическое описание объектов ai Для любых элементов множеств рассмотренные отношения будем описывать с помощью предикатов (логических функций), которые при подстановке на место предметных переменных x1, x2, Например, рассматривается подмножество групп поверхностей детали An. Необходимо выделить из него множество тех n-к (a1,…,an), у которых между элементами установлен порядок следования, истинный с точки зрения технологической сущности задачи. Из закономерностей технологии машиностроения принимаем, что если качество поверхности aj выше качество поверхности ai, то обработка поверхности ai предшествует обработки поверхности аj, т.е. из
Операция навешивания ограниченных кванторов общности и существования позволяет задать область, определяющую значения истинности для приведенных формул. Применив те же условия к множеству С, получим множество тех пар, которые удовлетворяют условию (1), и, дополнив его условием транзитивности получим функцию выделения подмножества Cm1 из Cm.
Физическая интерпретация в этом случае такова: средства, дающие более качественную обработку, следуют в порядке обработки за средствами, дающими менее качественную обработку. Рассмотрим условия, с помощью которых определяются те элементы. Которые связаны отношением совместности. Обозначим совместимость двух поверхностей аi и aj через аi ↔ aj. Это условие может быть выведено из реального условия возможности обработки нескольких поверхностей в одной операции. Например, поверхности, обладающие одними и теми же свойствами
Условие совместности элементов множества А запишем функцией (3), где MA – множество значений свойств обрабатываемых поверхностей;
Отношение совместности имеет место и на множестве С. Условие истинности отношения совместимости между элементами какой-либо пары (c1,c2) на C2 может быть установлено из реального условия возможности применения технических средств на одном этапе обработки (в переходе или операции). Например, в одном переходе можно применять токарный станок и резец (они совместны в обработке), но нельзя использовать токарный станок и фрезу (они несовместны в обработке). Совместность средств обработки может быть определена по их свойствам. Рассматривая взаимодействие технологических предметов в процессе обработке, определим, что существует взаимодействие, выраженное в том, что обрабатываемая поверхность, станок, инструмент, режимы резания, оснастка, базовая поверхность могут быть одновременно использованы на одном и том же этапе процесса изготовления. Например, в одном переходе используются: базовая поверхность, обрабатываемая поверхность, станок, инструмент и оснастка, необходимые для её обработки. Будем называть эти технологические предметы совместными в обработке или предметами, между которыми установлено отношение совместности. Для обозначения отношения совместности будем использовать символ ↔: х ↔ y или Qt2(x,y) В отличие от рассмотренного выше отношения следования отношения совместности имеет место между различными предметами, а именно между поверхностью и станком, между поверхностью и инструментом, между поверхностью и базовой поверхностью, между поверхностью и оснасткой, между станком и инструментом, между станком и оснасткой, между базовой поверхностью и оснасткой. Рассматривая взаимосвязь различных технологических предметов легко установить, что существуют такие предметы, когда один предмет «или несколько» предопределяет наличие, употребления другого предмета в технологическом процессе. Например, использование токарного станка предопределяет использование токарных инструментов (резцов различного профиля). Поверхность вращения предопределяет необходимость использования станков, на которых можно обрабатывать эти поверхности, а именно: токарных, сверлильных, револьверных и т.п.. Для обозначения отношения предопределения будем употреблять символ →:
х → y или Qt3(x,y) Отношение предопределения также, как и отношение совместности, существует лишь между различными предметами, а именно: обрабатываемая поверхность предопределяет станок, инструмент, базу, режим резания и оснастку; станок – инструмент, режим резания и оснастку; инструмент – режим резания и оснастку; база – определенную оснастку. Итак, можно сделать вывод, что между технологическими предметами и их свойствами существует отношение принадлежности; между технологическими предметами имеются отношения следования, совместности и предопределения. В процессе проектирования технолог изучает свойства технологических предметов и, выбирая необходимые, сравнивает их между собой. Одни свойства имеют в технологии цифровые значения, например, квалитет точности, геометрические параметры и т.п.; другие, такие, как вид поверхности и т.п., имеют словесные наименования. Для сравнения цифровых значений свойств достаточно рассмотреть лишь два отношения: равенство (=), например, [m1] = [m2] или Rt2(m1, m2) и неравенства, которые будем обозначать символом (<), например, [m1]<[m2] или Rt1(m1, m2). Для свойств, не имеющих в технологии количественных характеристик, будем определять отношения равенств Rt2 и неравенства Rt2. Еще раз отметим, что арифметическое отношение меньше (<) имеет место лишь для значений свойств, а отношение равенства Rt2 будем употреблять для цифровых значений (наименований) свойств и предметов. Определение областей существования отношений проведем с помощью логического анализа технологических законов, правил и утверждений. В технологическом описании проектирования технологических процессов, как правило, не встречаются в явном виде утверждения в тех формулировках, которые мы будем рассматривать ниже, но, анализируя технологические знания, эти утверждения можно выделить. Рассмотрим те утверждения, в которых идет речь о наличии (существовании) отношений между предметами. Утверждение 1. Каждый технологический предмет обладает хотя бы одним свойством. Используя символику логики предикатов, запишем это утверждение в виде
Т М где Рассмотрим, для каких подмножеств Т и М записанное высказывание состоит из истинных элементарных высказываний. Множество Т технологических предметов включает в себя следующие подмножества: T1 - множество станков, Т2 - множество инструментов, Т3 - множество режимов резания, Т4 -, множество оснастки, Т5 - множество обрабатываемых поверхностей (поверхностей детали), Т6 - множество базовых поверхностей. Таким образом, Т = T1 U T2 U Т3 U Т4 U Т5 U Т6. Множество М свойств технологических предметов включает: М1 - множество свойств станков, М2 - множество свойств инструментов, М3 - множество свойств режимов резания, М4 - множество свойств оснасток, М5 - множество свойств обрабатываемых поверхностей, М6 - множество свойств базовых поверхностей.
Утверждение 2. Каждый технологический предмет связан каким-либо отношением Qt с другим технологически предметом:
Т T Утверждение 3. Для каждого технологического предмета найдется другой, который совместен с первым в процессе обработки:
Т T Утверждение 4. Существуют технологические предметы, которые предопределяют друг друга в технологическом процессе обработки:
Т T Технологические утверждения содержат описание условий, правильных сточки зрения технологии и производства, выраженные через взаимодействия между предметами и их свойствами. В условиях описываются взаимодействия сточки зрения требований основного служебного назначения и других классов требований. Математическое описание технологических утверждений позволяет выразить в формализованном виде целевые установки по проектированию технологии и закономерности их достижения, обеспечивающем в дальнейшем их построение с помощью формальных процедур. В математическом описании технологических утверждений используются основные логические зависимости, полученные ранее. Все технологические предметы взаимосвязаны. Взаимосвязь задается в следующем виде: если имеется какой-либо предмет с определенными свойствами, то он предполагает наличие другого технологического предмета с определенными свойствами. Например, наличие поверхностей вращения предполагает наличие станков, допускающих обработку таких поверхностей, токарных, сверлильных, револьверных и т. п. Аналогично могут быть записаны зависимости других параметров станка и инструмента от свойств обрабатываемой поверхности. Теперь рассмотрим утверждения, из которых могут быть определены условия правильных, с точки зрения технологии, взаимодействий различных технологических предметов в технологическом процессе. Ранее мы выразили эти взаимодействия в виде отношений следования, совместности и предопределения. Исследуем, при каких условиях выполняется отношение следования. Проанализируем следующие технологические утверждения: поверхности наивысшего качества обрабатывают на последних этапах обработки, черновая обработка предшествует чистовой обработке, более точные станки применяют после менее точных и т. п. Из этих утверждений следует, что основой упорядочения технологических предметов является свойство качества. Предмет с более низким качеством предшествует в процессе обработки предмету с более высоким качеством. Для обрабатываемых поверхностей эта зависимость имеет вид
Т5 T 5 M25 M25 Т.е. формула описывает следующие условия: 1) если два предмета обладают такими значениями качества, что одно из них меньше другого, то предмет, обладающий худшим качеством, предшествует в процессе обработки предмету, обладающему более высоким качеством; 2) для каждого предмета существует другой предмет, связанный с первым отношением следования. Рассмотрим, при каких условиях между предметами выполняется отношение совместности. Как было определено выше, предметы совместны, если используются на одном и том же этапе обработки. Использование средств обработки предопределено свойствами обрабатываемых поверхностей. В этой связи рассмотрим условия выполнения отношения предопределения, а затем отношения совместности. Пусть имеется обрабатываемая поверхность (плоскость), которая по своим свойствам требует использования соответствующего станка (например, вертикально-фрезерного). Из технологической практики известно, что такие свойства обрабатываемой поверхности, как вид поверхности, ее качество (квалитеты точности и шероховатость), положение поверхности и ее соотношение с другими поверхностями, предопределяют тот метод или методы обработки, которыми должны обладать средства обработки, станок и инструмент. Таким образом, поверхность с определенными свойствами предопределяет станок и инструмент с определенным методом обработки, следовательно, поверхность предопределяет станок и инструмент. Выбранный метод обработки, а также такие свойства обрабатываемой поверхности, как вид поверхности, положение и соотношение с другими поверхностями, позволяют определить еще одно свойство станка, а именно его вид. Вид станка, выбранный метод обработки, а также свойства обрабатываемой поверхности позволяют определить вид инструмента. Таким образом, условием наличия отношения предопределения между поверхностью, станком и инструментом является наличие определенной зависимости между свойствами станка, обрабатываемой поверхности и инструмента. Исходя из рассмотренных утверждений, можно сделать вывод, что совместность технологических предметов в процессе обработки может быть записана формулой, которую можно использовать в процедурах автоматизации процессов проектирования.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 508; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.105.101 (0.014 с.) |

 A, ci
A, ci 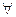 (обобщение операций конъюнкции) и существования – знак
(обобщение операций конъюнкции) и существования – знак  (обобщение операции дизъюнкции).
(обобщение операции дизъюнкции). 1,
1, 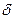 x ≤ N, где N - заданное число или числовое выражение.
x ≤ N, где N - заданное число или числовое выражение. – операция конъюнкции, знак
– операция конъюнкции, знак  – операция импликации,
– операция импликации,  – операция дизъюнкции.
– операция дизъюнкции.


