
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи моделирования. Виды моделейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Под моделированием понимается исследование объектов познания не непосредственно, а косвенным путем, при помощи анализа некоторых других вспомогательных объектов. Такие вспомогательные объекты и будем называть моделями. Модели выбираются таким образом, чтобы они были значительно проще для исследования, чем рассматриваемые объекты. Более того, некоторые объекты вообще не удается исследовать, т.е. провести эксперимент. В модели воспроизводятся лишь некоторые наиболее важные свойства исходного объекта. В процессе проектирования новой или модернизации существующей технической системы решаются задачи расчета параметров и исследования процессов в этой системе. При проведении многовариантных расчетов реальную систему заменяют моделью. В широком смысле модель определяют как отражение наиболее существенных свойств объекта. Моделирование позволяет решить четыре различных задачи: · визуализировать систему в ее текущем или желательном для нас состоянии; · определить структуру или поведение системы; · получить шаблон, позволяющий затем сконструировать систему; · документировать принимаемые решения, используя полученные модели. Математическая модель технического объекта - совокупность математических объектов и отношений между ними, которая адекватно отражает свойства исследуемого объекта, интересующие исследователя (инженера). Следует иметь в виду, что любой объект не может существовать обособленно, без взаимосвязи с другими объектами (окружающей средой). Для процесса резания элементами окружающей среды являются обрабатываемый и инструментальный материалы, смазочно-охлаждающая жидкость, образующаяся в результате обработки стружка и т.д. Для технологического процесса в ходе его реализации - это технологическое оборудование, режущий инструмент, элементы приспособления и т.д. Для технологической системы (механического участка из универсальных станков или станков с ЧПУ, автоматической линии и др.) элементами окружающей среды являются другие технологические системы, цеховой транспорт и т.д. Структурная схема объекта моделирования представлена на рис.1.1.
Рис.1.1. Структурная схема объекта моделирования
Объектами моделирования в машиностроительном производстве являются:
1. Технические системы (ТС) – станки, участки из универсальных станков, автоматические линии, гибкие производственные системы (ГПС). 2. Технологические процессы (ТП). 3. Физические процессы (ФП) – процессы, протекающие при резании металлов, при функционировании технологического оборудования. 4. Экономические процессы предприятий. Математические модели разрабатываются для решения следующих задач: - исследования технических систем физических и технологических процессов. - проектирования технических систем и технологических процессов. - оптимизации в ходе проектирования технологических процессов, технических систем и организации производства. - построения систем автоматизированного проектирования технологий. Вид, состав, сложность математической модели зависит от того, какой объект она описывает и для каких целей разработана. Особенностями технологии машиностроения, которые не позволяет в полной мере использовать современные вычислительные средства и методы компьютерного моделирования являются: - отсутствие строгих аналитических зависимостей (ряд существующих в технологии правил имеет рекомендательный характер); - сложная взаимосвязь и взаимное влияние отдельных задач; - наличие огромных информационных потоков. Наиболее важная и сложная задача машиностроительного производства - это проектирование технологических процессов механической обработки и сборки. Для применения ЭВМ в проектировании технологии должен быть формализован процесс проектирования, т.е. необходима замена содержательных предложений формулами, их выражающими, что и подразумевает математическое моделирование. При технологическом проектировании необходимо использовать большой объем информации самой разнообразной формы и содержания, которая перерабатывается в процессе проектирования с целью принятия решения. Вся эта информация, представленная в формальном виде, составляет информационное обеспечение. Повышение качества получаемых проектных решений связано с использованием в составе информационного обеспечения баз знаний (БЗ). Основные задачи, которые предполагает формирование БЗ: 1. Описание информации, необходимой для решения и автоматизации задач технологического проектирования.
2. Возможность анализа проектных заданий. 3. Поддержка процесса взаимодействия проектировщика с системой. Развитие БЗ позволяет имитировать деятельность человека при решении широкого класса задач автоматизированного проектирования, осуществлять поиск в пространстве возможных решений. Несмотря на эвристический характер многих операций моделирование имеет ряд положений и приемов, общих для получения моделей различных объектов. Достаточно общий характер имеют: · методика макро моделирования, · математические методы планирования экспериментов, · алгоритмы формализуемых операций расчета численных значений параметров и определения областей адекватности. Получение моделей в общем случае - процедура неформализованная. Основные решения, касающиеся выбора вида математических соотношений, характера используемых переменных и параметров, принимает проектировщик. В тоже время такие операции, как расчет численных значений параметров модели, определение областей адекватности и другие, алгоритмизированы и решаются на ЭВМ. При составлении математической модели от исследователя требуется: · изучить свойства исследуемого объекта; · умение отделить главные свойства объекта от второстепенных; · оценить принятые допущения. Модель, реализуемая на ЭВМ, описывает зависимость между исходными данными и искомыми величинами. Последовательность действий, которые надо выполнить, чтобы от исходных данных перейти к нужным искомым величинам, называют алгоритмом. Схема использования математической модели в системе автоматизированного проектирования показана на рис. 1.2. Вычислительная мощность современных компьютеров в сочетании с предоставлением пользователю всех ресурсов системы, возможностью диалогового режима при решении задачи и анализе результатов позволяют свести к минимуму время решения задачи.
Рис. 1.2. Использование математических моделей в САПР Модели и моделирование применяются по основным направлениям: · обучение (как моделям, моделированию, так и самих моделей); · познание и разработка теории исследуемых систем (с помощью каких-либо моделей, моделирования, результатов моделирования); · прогнозирование (выходных данных, ситуаций, состояний системы); · управление (системой в целом, отдельными подсистемами системы), выработка управленческих решений и стратегий; · автоматизация (системы или отдельных подсистем системы). Пример 1. Рассмотрим физическую систему: тело массой m скатывающееся по наклонной плоскости с ускорением a, на которое воздействует сила F. Исследуя такие системы, Ньютон получил математическое соотношение: F=ma. Это физико-математическая модель системы или математическая модель физической системы. При описании этой системы (построении этой модели ) приняты следующие гипотезы: 1) поверхность идеальна (т.е. коэффициент трения равен нулю); 2) тело находится в вакууме (т.е. сопротивление воздуха равно нулю); 3) масса тела неизменна; 4) тело движется с одинаковым постоянным ускорением в любой точке. Пример 2. Совокупность предприятий функционирует на рынке, обмениваясь товарами, сырьем, услугами, информацией. Если описать экономические законы, правила их взаимодействия на рынке с помощью математических соотношений, например, системы алгебраических уравнений, где неизвестными будут величины прибыли, получаемые от взаимодействия предприятий, а коэффициентами уравнения будут значения интенсивностей таких взаимодействий, то получим математическую модель экономической системы, т.е. экономико-математическую модель системы предприятий на рынке.
Пример 3. Если банк выработал стратегию кредитования, смог описать ее с помощью экономико-математических моделей и прогнозирует свою тактику кредитования, то он имеет большую устойчивость и жизнеспособность. Изучив тему, приведите примеры известных вам моделей объектов и процессов машиностроительного производства.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ: 1. Что понимается под процессом моделирования? 2. Какие задачи позволяет решить моделирование? 3. Что является объектами моделирования в машиностроении?
1.2 Классификация математических моделей Классификация в любой области знаний чрезвычайно важна. Она позволяет обобщить накопленный опыт, упорядочить понятия предметной области. Математические модели классифицируются по ряду признаков. В таблице 1.1 представлены виды математических моделей по различным признакам классификации. Таблица 1.1 Классификация математических моделей
Приведенная классификация математических моделей может быть применена по отношению к любым объектам. Рассмотрим особенности различных видов моделей применительно к объектам (процессам) в машиностроении. Математические модели на микроуровне производственного процесса отражают физические процессы, протекающие, например, при резании металлов. Они описывают процессы на уровне технологического перехода (прохода). Анализ таких моделей сводится к решению краевых задач математической физики. Аппарат уравнений математической физики описывает тепловые процессы или напряженно-деформированное состояние детали. Математические модели на макроуровне.
На макроуровне производится дискретизация пространства и переход к сосредоточенным моделям. Элементами этого уровня являются объекты, которые на микроуровне рассматривались как системы. Например, при сборке машины любая сборочная единица рассматривается как элемент, хотя представляет собой систему, состоящую из отдельных элементов- деталей. На метауровне с помощью дальнейшего абстрагирования от характера физических процессов удается получить приемлемое по сложности описание процессов, протекающих в используемых объектах. Математический аппарат на метауровне – теория множеств, математическая логика, теория массового обслуживания. Структурные математические модели предназначены для отображения структурных свойств объектов и используются в тех случаях, когда можно абстрагироваться от особенностей физических процессов протекающих в объекте. Например, в САПР ТП для полного представления структуры технологического процесса, технологической операции используются структурно – логические модели. Функциональные математические модели предназначены для отображения информационных, физических, временных процессов, протекающих в работающем оборудовании, в ходе выполнения технологических процессов и т.д. Они чаще всего имеют форму системы уравнений. Аналитические математические модели представляют собой явные математические выражения выходных параметров как функций от параметров входных и внутренних. Это, например, выражения для определения сил резания. Аналитическое моделирование основано на косвенном описании моделируемого объекта с помощью набора математических формул. Язык аналитического описания содержит следующие основные группы семантических элементов: критерий (критерии), неизвестные, данные, математические операции, ограничения. Наиболее существенная характеристика аналитических моделей заключается в том, что модель не является структурно подобной объекту моделирования. Под структурным подобием здесь понимается однозначное соответствие элементов и связей модели элементам и связям моделируемого объекта. К аналитическим относятся модели, построенные на основе аппарата математического программирования, корреляционного, регрессионного анализа. Аналитическая модель всегда представляет собой конструкцию, которую можно проанализировать и решить математическими средствами. Так, если используется аппарат математического программирования, то модель состоит в основе своей из целевой функции и системы ограничений на переменные. Целевая функция, как правило, выражает ту характеристику объекта (системы), которую требуется вычислить или оптимизировать. В частности, это может быть производительность технологической системы. Переменные выражают технические характеристики объекта (системы), в том числе варьируемые, ограничения – их допустимые предельные значения. Аналитические модели являются эффективным инструментом для решения задач оптимизации процессов, протекающих в технологических системах, а также оптимизации и вычисления характеристик самих технологических систем.
Важным моментом является размерность конкретной аналитической модели. Часто для реальных технологических систем (автоматических линий, гибких производственных систем) размерность их аналитических моделей столь велика, что получение оптимального решения оказывается весьма сложным с вычислительной точки зрения. Для повышения вычислительной эффективности в этом случае используют различные приемы. Один из них связан с разбиением задачи большой размерности на подзадачи меньшей размерности так, чтобы автономные решения подзадач в определенной последовательности давали решение основной задачи. При этом возникают проблемы организации взаимодействия подзадач, которые не всегда оказываются простыми. Другой прием предполагает уменьшение точности вычислений, за счет чего удается сократить время решения задачи. Алгоритмические математические модели выражают связи между выходными параметрами и параметрами входными и внутренними в виде алгоритма. Имитационные математические модели – это алгоритмические модели, отражающие развитие процесса (поведение исследуемого объекта) во времени при задании внешних воздействий на процесс (объект). Например, это модели систем массового обслуживания, заданные в алгоритмической форме. Имитационное моделирование основано на прямом описании моделируемого объекта. Существенной характеристикой таких моделей является структурное подобие объекта и модели. Это значит, что каждому существенному с точки зрения решаемой задачи элементу объекта ставится в соответствие элемент модели. При построении имитационной модели описываются законы функционирования каждого элемента объекта и связи между ними. Работа с имитационной моделью заключается в проведении имитационного эксперимента. Процесс, протекающий в модели в ходе эксперимента, подобен процессу в реальном объекте. Поэтому исследование объекта на его имитационной модели сводится к изучению характеристик процесса, протекающего в ходе эксперимента. Ценным качеством имитации является возможность управлять масштабом времени. Динамический процесс в имитационной модели протекает в так называемом системном времени. Системное время имитирует реальное время. При этом пересчет системного времени в модели можно выполнять двумя способами. Первый способ заключается в «движении» по времени с некоторым постоянным шагом. Второй способ заключается в «движении» по времени от события к событию, при этом считается, что в промежутках времени между событиями в модели изменений не происходит. Теоретические математические модели создаются в результате исследования объектов (процессов) на теоретическом уровне. Например, существуют выражения для сил резания, полученные на основе обобщения физических законов. Но они не приемлемы для практического использования, т.к. очень громоздки и не совсем адаптированы к реальным процессам обработки материалов. Эмпирические математические модели создаются в результате проведения экспериментов (изучения внешних проявлений свойств объекта с помощью измерения его параметров на входе и выходе) и обработки их результатов методами математической статистики. Детерминированные математические модели описывают поведение объекта с позиций полной определенности в настоящем и будущем. Примеры таких моделей: формулы физических законов, технологические процессы обработки деталей и т.д. Вероятностные математические модели учитывают влияние случайных факторов на поведение объекта, т.е. оценивают его будущее с позиций вероятности тех или иных событий. Примеры таких моделей: описание ожидаемых длин очередей в системах массового обслуживания, ожидаемых объемов выпуска сверхплановой продукции производственным участком, точности размеров в партии деталей с учетом явления рассеяния и т. д. Аналоговые математические модели – это модели, свойства которых определяются законами изучаемой системы, а переменные и параметры – непрерывные величины. Дискретные математические модели – это модели, в которых все переменные и параметры являются дискретными величинами. Основные свойствалюбой модели: · целенаправленность - модель всегда отображает некоторую систему, т.е. имеет цель; · конечность - модель отображает оригинал лишь в конечном числе его отношений и, кроме того, ресурсы моделирования конечны; · упрощенность - модель отображает только существенные стороны объекта и, кроме того, должна быть проста для исследования или воспроизведения; · приблизительность - действительность отображается моделью грубо или приблизительно; · адекватность - модель должна успешно описывать моделируемую систему; · наглядность, обозримость основных ее свойств и отношений; · доступность и технологичность для исследования или воспроизведения; · информативность - модель должна содержать достаточную информацию о системе (в рамках гипотез, принятых при построении модели) и должна давать возможность получить новую информацию; · полнота - в модели должны быть учтены все основные связи и отношения, необходимые для обеспечения цели моделирования; · устойчивость - модель должна описывать и обеспечивать устойчивое поведение системы, если даже она вначале является неустойчивой; · целостность - модель реализует некоторую систему (т.е. целое); · замкнутость - модель учитывает и отображает замкнутую систему необходимых основных гипотез, связей и отношений; · адаптивность - модель может быть приспособлена к различным входным параметрам, воздействиям окружения; · управляемость (имитационность) - модель должна иметь хотя бы один параметр, изменениями которого можно имитировать поведение моделируемой системы в различных условиях; · эволюционируемость - возможность развития моделей (предыдущего уровня). Процедура построения математической модели включает следующие этапы: - выбор свойства объекта, которые подлежат отражению в модели, а также установление универсальности модели; - сбор исходной информации о свойствах моделируемого объекта, - получение общего вида математических соотношений модели, - определение числовых значений параметров модели, - оценка точности полученной модели и определение ее адекватности. ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ: 1. По каким признакам производится классификация моделей? 2. Перечислите способы представления свойств объекта моделирования. 3. Какие модели используются на микро- и макроуровнях исследования производственных процессов?
1.3 Требования к математическим моделям К математическим моделям предъявляются следующие основные требования: 1. Универсальности. 2. Точности. 3. Адекватности 4. Экономичности. Универсальность математической модели характеризует полноту отражения в ней свойств реального объекта. Математическая модель отражают не все, а лишь некоторые свойства реального объекта. Например, формулы для сил резания, которые приведены в лекции 1, не учитывают температуру окружающего воздуха, влажность, экономические параметры и т.д. Точность математической модели оценивается степенью совпадения значений выходных параметров реального объекта и значений тех же параметров, рассчитанных с помощью модели. Пусть отражаемые в математической модели свойства объекта оцениваются вектором выходных параметров
По этой формуле рассчитываются погрешности для каждого выходного параметра, в результате получается вектор погрешностей
Например, оценим погрешность рассмотренной в лекции 1 математической модели. Вектор выходных параметров Адекватность математической модели – это ее способность отражать заданные свойства объекта с погрешностью, не выше заданной. Т. к. выходные параметры модели являются функцией
где Экономичность математической модели характеризуется затратами вычислительных ресурсов на ее реализацию. Если работа с математической моделью осуществляется вручную, то ее экономичность определяется затратами личного времени проектировщика. Если модель используется при автоматизированном проектировании, то затратами машинного времени и памяти компьютера. Так как указанные величины определяются характеристиками конкретного компьютера, то использовать их для оценки экономичности математической модели не корректно. Поэтому, для оценки экономичности самой математической модели используют другие величины: 1. Среднее количество операций, выполняемых при одном обращении к математической модели. 2. Размерность системы уравнений в математической модели. 3. Количество используемых в модели внутренних параметров и т.д. Требования высокой степени универсальности, точности, широкой области адекватности математической модели, с одной стороны, и высокой ее экономичности, с другой стороны, противоречивы. Поэтому компромиссные решения определяются решаемой задачей. К математическим моделям предъявляется и целый ряд других требований, среди которых следует выделить следующие: 1. Вычислимость, т.е. возможность ручного или с помощью ЭВМ исследования качественных и количественных закономерностей функционирования объекта (системы). 2. Модульность, т.е. соответствие конструкций модели структурным составляющим объекта (системы). 3. Алгоритмизируемость, т.е. возможность разработки соответствующих алгоритма и программы, реализующей математическую модель на ЭВМ. 4. Наглядность, т.е. удобное визуальное восприятие модели. ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ: 1. Перечислите требования к математическим моделям. 2. Как оценивается адекватность математических моделей? 3. По каким параметрам можно оценить экономичность математических моделей?
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 6796; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.147.121 (0.016 с.) |



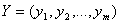 ,
,  - i-ый параметр, рассчитанный с помощью модели, а
- i-ый параметр, рассчитанный с помощью модели, а 
 - истинное значение того же параметра. Тогда относительная погрешность математической модели по i – му параметру будет равна:
- истинное значение того же параметра. Тогда относительная погрешность математической модели по i – му параметру будет равна:
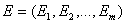 . В целом для математической модели погрешность оценивается следующим образом:
. В целом для математической модели погрешность оценивается следующим образом: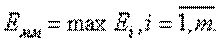
 . Пусть
. Пусть 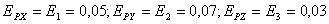 ; тогда в целом погрешность математической модели
; тогда в целом погрешность математической модели 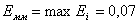 .
. от параметров внутренних и входных, то и точность модели зависит от их значений. Адекватность модели имеет место в ограниченной области изменения внутренних и входных параметров. Если обозначить область адекватности как
от параметров внутренних и входных, то и точность модели зависит от их значений. Адекватность модели имеет место в ограниченной области изменения внутренних и входных параметров. Если обозначить область адекватности как  , то
, то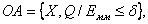
 - некоторое заданное число.
- некоторое заданное число.


