
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цели и задачи эконометрического анализа. Классификация и основные типы моделей.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цели и задачи эконометрического анализа. Классификация и основные типы моделей. Основана на 3 напрвлениях: ЭТ, Мат методы, стат теория. Цель: придание кол-ого выражения общим закон-тям ЭТ на БД стат наблюдений с исп-ния мат стат инструментария. Задачи: анализ причинно-следств связей между эк переменными; прогноз показателей в экономике; имитация разл возм сценариев соц-эк развития анализируем системы. Использование в: макроэк-ка, монетарная эк-а, межд эк-а, фин рынки, микроэкономика. Классификация данных моделей: пространств(совокупность значений полученные из некот группы n>1 объектов в фиксир момент времени), времен(упорядочен мн-во, хар-щее изменение показ-лей во времени), панельные(сочетание пространств и временных). Общий вид модели: пусть состояние некот эконом процесса или явления в момент времени t харак-ся перемен yt, следовательно, зависимая переменная(эндогенная). Состояние процесса зависит от ф-ров: 1)случайные неконтролируемые ф-ры, приводящ к случ отклонениям Et значения эндогенной переменной yt от ее ожид значения. 2) систематич контролируемые наблюд ф-ры, представляемые объясняющими переменными, значения кот считаются известными ко времени t: лаговые или предопр-ные переменные y t-1,y t-2…y t-l; экзоген переменные x t1, x t2, …, x tk харак-ют воздействие на процесс со стороны контрол факторов.
Где f(_) - функция определенная с точностью до неизвестных параметров При построении (1) решаются задачи: найти Модель вида (1) используется для анализа зависимости эндоген перемен от включения в модель экзоген перемен; для прогнозирования; для выбора значения экзоген перемен, обеспечивающих достижения заданных целевых значений эндоген переменных. Осн типы моделей: а) размерноть модели: одномерные, многомерные(последние делятся на структурные и неструктурные). б) фактор времени: статические(к 1 периоду времени), динамич(лаговые, времен ряды). в) вид зависимости: линейн по параметрам, нелинейн, внутри-линейн. Пример модели(модель спроса и предложения)
(модель временного ряда)
Этапы построения эконометрических моделей.
1. Эконометрическое обоснование модели: · формулируется задача и цель исследования, состав эндо- и экзогенных переменных для включения в модель; · производится оценка возможностей получения статистических данных определенного объема и интервалов наблюдения; · производится анализ взаимосвязей между переменными; · разрабатывается общая структура эконометрической модели. 2. Подготовка статистических данных: · сбор и накопление необходимого набора данных; · представление значений переменных в требуемом виде; · предварительный анализ данных для выявления особенностей. 3. Построение и анализ адекватности модели: · спецификация модели; · статистическое оценивание параметров модели по имеющимся данным; · тестирование адекватности построенных моделей на основе тестовых статистик и переменных; · тестирование гипотез, предполагаемых в экономической теории. 4. Использование модели: · интерпретация полученных результатов; · реализация модели для прогноза и построения сценариев развития исследуемых процессов.
Проверка гипотезы об улучшении качества регрессионного уравнения. Предполагается, что сначала оценивается регрессия с k переменными и объясняется сумма квадратов состояний RSSk . Затем в модель добавим еще несколько переменных и доведем общее значение экзогенных переменных до m: RSSm. Таким образом, мы объясняем дополнительные величины RSSm – RSSk и используем при этом (m – k) степеней свободы. Следует выяснить, превышает ли данное увеличение то, которое может быть получено случайно.
Если
Гетероскедастичность (Г): причины, последствия. Графический метод обнаружения. Во многих эконометрических исследованиях предположение о постоянстве дисперсии (гомоскедастичность) оказывается нереалистичным. Непостоянство дисперсии – гетероскедастичность. Причина: неоднородность данных. При изучении бюджета потребителей можно заметить, что дисперсия растет с ростом доходов. Последствия Г: 1)оценки коэффициентов остаются несмещенными и линейными, однако перестают быть эффективными. 2) дисперсии оценок будут рассчитываться со смещениями, вполне вероятно, что t-статистика будет завышена.
Обнаружение Г: 1) графический анализ отклонений. 2) тест ранговой корреляции Спирмена. 3) тест Парка, Глейзера, Уайта, Бреуша-Пагана, Голдфельда-Кванда. Графический метод. По оси у -
а) b) c) d) e)
a) – нет Г. b) - e) – есть Г.
Метод рядов Последовательно определяются знаки отклонений еt. Например, (-----)(+++++++)(---)(++++)(-), т. е. 5 “-“, 7 "+", 3 “-“, 4 "+", 1 "-" при 20 наблюдениях. Ряд определяется как непрерывная последовательность одинаковых знаков. Количество знаков в ряду называется длиной ряда. Визуальное распределение знаков свидетельствует о неслучайном характере связей между отклонениями. Если рядов слишком мало по сравнению с количеством наблюдений n, то вполне вероятна положительная автокорреляция. Если же рядов слишком много, то вероятна отрицательная автокорреляция. Для более детального анализа предлагается следующая процедура. Пусть n - объем выборки; n1 - общее количество знаков при n наблюдениях (количество положительных отклонений et); n2 - общее количество знаков "—" при n наблюдениях (количество отрицательных отклонений et); к - количество рядов. При достаточно большом количестве наблюдений (n1 > 10, n2 > 10) и отсутствии автокорреляции случайная величина k имеет асимптотически нормальное распределение с
Тогда, если M(k) - uα\2*D(k) < k < M(k) + uα/2*D(k), то гипотеза об отсутствии автокорреляции не отклоняется. Тест Дарбина-Уотсона Предполагаем, что случайная последовательность
H0: H1:
На практике вместо коэффициента корреляции используется статистика Дарбина-Уотсона:
Очевидно, что эта статистика связана с коэффициентом корреляции R:
Критическое значение DW зависит от n, k и Выводы по тесту Д-У: На практике применение критерия Дарбина — Уотсона основано на сравнении величины 1. Если 2. Если 3. Если Когда расчетное значение Также с помощью данного критерия выявляют наличие коинтеграции между двумя временными рядами. В этом случае проверяют гипотезу о том, что фактическое значение критерия равно нулю. С помощью метода Монте-Карло были получены критические значения для заданных уровней значимости. В случае, если фактическое значение критерия Дарбина — Уотсона превышает критическое, то нулевую гипотезу об отсутствии коинтеграции отвергают.
Ограничения при использовании: 1) только для тех моделей, которые содержат свободный член; 2) случайные отклонения определяются авторегрессионной схемой первого порядка; 3) статистические данные должны иметь одинаковую периодичность; 4) не применяется для моделей, содержащих в составе объясняющих переменных зависимую переменную с временным лагом 1.
Фиктивные переменные y=Xb+E, где b-это бета и является определителем линейности. В модели влияние кач-го фактора выраж-ся в виде фиктивной пер-ой. Примеры исп-я фиктивных пер-х: 1) Непосредственное описание кач-го признака 2) Исследование сезонных колебаний 3) Исследование эффекта сдвига времени или сезонные изменения Пример 1 Введем возьмем мат. ожидание от обеих частей уравнения: таким образом величина гамма переходе от одной категории в другою при неизменном знач. остальных факторов. Корректор сезонных колебание для описания сезонных колебаний во временных рядах широко используются фиктивные переменные: для квартальных данных: 3 фиктивные переменные, Множественная сов-сть эф-ных пер-х Предположим, что используем за определенное время (по сезонам), то есть кварталы, потребление q некоторого товара, задается некорая функция учитывающая сезонные колебания и влияние различий в соц. группах.
где если модель относится к семье из 1-й соц. группы, 2 квартал => Исследовании структурных изменений Допустим у нас есть временной ряд Пусть в t0 произошла структурная перестройка, r-фиктивная переменная.
Тестируя гипотезу проверяем, что струкрур изменения не произошли, но Взаимодействия между фик. пер-ми 1) Для моделирование выброса эф-ных пер-ных можно использ. след. образом. 2) Для моделировании измен. тренда
Оценивание СОУ. Косвенный Метод Наименьших Квадратов (КМНК) – один из способов решения СОУ. Он включает последовательность шагов: 1.Исходя из структурных уравнений строятся уравнения приведённой формы. 2. С помощью МНК оцениваются параметры уравнений приведённой формы. 3. На основе полученных оценок находятся параметры структурных уравнений. Рассмотрим КМНК на примере модели:
Пример для случая идентифицируемости. Запишем приведённую форму:
C помощью МНК находим оценки неизвестных параметров a’ и b’:
В результате получаем:
Подробнее о случаях идентифицируемости, неидентифицируемости и сверхидентифицируемости смотрите в 18-м вопросе. Двухшаговый МНК (ДМНК) применяется в тех случаях, когда уравнение сверхидентифицируемо. Алгоритм: 1. Составляется приведённая форма модели и определяются численные значения параметров с помощью МНК. 2. Рассматриваются теоретические знания эндогенных переменных. 3. Обычным МНК определяются параметры структурного уравнения, используя в качестве исходных данных расчётные значения предопределённых переменных, стоящих в правой части уравнения. Замечание. Если условие идентифицируемости для уравнения выполнено со знаком равенства, то оценка, полученная с помощью ДМНК, совпадает с оценкой, полученной с помощью КМНК.
Единая методика расчета. 4) Несопоставимость показателей возникает в силу неодинаковости применяемых единиц измерения. 5) Приведение уровней ряда к сопоставимым ценам. 6) Необходимо учитывать однородность данных. При решении практических задач достаточно часто переходят от уровней ряда к экономическим индексам. Форма представления экономических индексов определяет классификацию временных рядов по следующим видам: 2. В уровнях ряда 3. В темпах роста с использованием данных по отношению к фиксированному периоду Т.
4. В темпах роста с использованием данных по отношению к предыдущему периоду
5. В темпах роста с использованием данных по отношению к соответствующему периоду предыдущего года.
6. В темпах роста с использованием данных нарастающим итогом с начала текущего года по отношению к данным нарастающим итогом с начала предыдущего года.
m= от i до k. i – номер года; k – число периодов в году. Первый показатель (1) представлен в базисной форме. Он характеризует динамику соотношений Показатель (2) представлен в цепной форме в виде темпа роста. Он является безразмерной величиной и может быть использован для сопоставления различных показателей. Составляющие динамики ВР В общем виде при исследовании экономического временного ряда
1. календарные эффекты (отклонения, связанные с определенными предсказуемыми календарными событиями); 2. выбросы (аномальные движения ВР, связанные с редко происходящими событиями, которые резко, но кратковременно отклоняют ряд от общего закона); 3. структурные сдвиги (аномальное движение ВР, связанное с редко происходящими событиями, имеющими скачкообразный характер и меняющиеся тенденции). Для моделирования структурных изменений используется фиктивные переменные, которые вводятся след. образом: - для моделирования сезонности: - для моделирования изменения тренда: - для моделирования аддитивных выбросов: Будем рассматривать ВР в след.виде: Анализ ВР заключается в выделении и изучении указанных компонент ряда в рамках аддитивной или мультипликативной моделях.
Представления ВР Под временным рядом понимается упорядоченное множество, характеризующее изменение показателя во времени. Элементы этого множества состоят из численных значений показателя, называемых уровнями временного ряда, и периодов – интервалов или моментов времени, к которым относятся уровни ВР. Если время изменяется непрерывно, то ВР называется непрерывным. Если же время фиксируется дискретно, то ВР называется дискретным. Дискретные ВР измеряются двумя способами: · выборка из непрерывных ВР через регулярные промежутки времени (моментные ряды) · накопление переменной в течение некоторого периода времени (интервальные ряды) Возможное значение ВР в данный момент времени t описывается с помощью случайной величины xt и связанного с ней распределения вероятности p(xt). Тогда наблюдаемое значение xt ВР в момент времени t рассматривается как одно из множества значений, которое могла бы принимать случайная величина. Однако, как правило, наблюдения ВР взаимосвязаны и для корректного его описания следует рассматривать совм. Вероятность p(x1, …, xt). Для правильного формирования ВР выдвигаются особые требования: · сопоставимость по территории (несопоставимость по территории возникает в результате изменения границ стран, регионов и хозяйств) · полнота охвата (требование одномоментной полноты охвата разных частей изучаемого объекта означает, что уравнение ряда за отдельные периоды должны характеризовать размеры того или иного явления по одному и тому же кругу входящих в его состав вещей) · единая методика расчёта · несопоставимость показателей возникает при неодинаковости применяемых единиц измерения · приведение уравнения ряда к сопоставимым ценам · необходимо учитывать неоднородность данных При решении практических задач переходят от уровней ряда к экономическим индексам. Форма представления экономических индексов определяет классификацию ВР по следующим видам: · В уравнениях ряда (xt) · В темпах роста с использованием данных по отношению к предыдущему периоду (It= xt/xT) – динамика соотношения xt между различными периодами некоторым фиксированным базисном периодом T; является безразмерной величиной; обеспечивает сопоставимость ВР · В темпах роста с использованием данных по отношению к соответствующему периоду предыдущего года (It= xt/xt-1) – цепная форма, используется модель регрессии с детерминированными факторами для моделирования ВР · В темпах роста с использованием данных с нарастающим итогом с начала текущего года по отношению к данным с нарастающим итогом с начала предыдущего года
Пример.
Коинтегрированные ряды. Пусть Если для В случае когда
В эконом-й теории значит-е место занимает понятие равновесия – состояния экономической системы при котором взаимодействие разнонаправленных сил взаимопогашается таким образом, что наблюдаемые свойства системы остаются неизменными. Пусть имеется n-мерный случайный вектор x компоненты нестационарного ВР.
Если экон-й системы сущ-ет сост-е равновесия, то эти переменные должны удовлетворять определённым ограничениям: Это тождество описывает зависимость м-ду переменными, кот-е имеют место в долгосрочной перспективе в сост-ии равновесия. В конкретный момент времени t может иметь место случайное отклонения от равновесного состояния, кот-е выр-ся следующим образом: Относительно Говорят что компоненты вектора x являются коинтегрированными порядка d,b. Обзначаются Если а) все компонентиы вектора x являются б) сущ-ет вектор
Подход Энгла—Грейнджера Простейшим методом отыскания стационарной линейной комбинации является метод Энгла—Грейнджера. Энгл и Грейнджер предложили использовать оценки, полученные из обычной регрессии с помощью метода наименьших квадратов. Одна из переменных должна стоять в левой части регрессии, другая—в правой: y t = β0+ β1xt + zt. Для того чтобы выяснить, стационарна ли полученная линейная комбинация, предлагается применить метод Дики—Фуллера к остаткам из коинтеграционной регрессии. Нулевая гипотеза состоит в том, что zt содержит единичный корень, т.е. y t и xt не коинтегрированы. Пусть zt —остатки из этой регрессии. Статистика Энгла—Грейнджера представляет собой обычную t -статистику для проверки гипотезы ϕ = 1 в этой вспомогательной регрессии. Распределение статистики Энгла—Грейнджера будет отличаться (даже асимптотически), от распределения DF-статистики, но имеются соответствующие таблицы. Если мы отклоняем гипотезу об отсутствии коинтеграции, то это дает уверенность в том, что полученные результаты не являются ложной регрессией. Игнорирование детерминированных компонент ведет к неверным выводам о коинтеграции. Чтобы этого избежать, в коинтеграционную регрессию следует добавить соответствующие переменные — константу, тренд, квадрат тренда, сезонные фиктивные переменные. Такое добавление, как и в случае критерия DF, меняет асимптотическое распределение критерия Энгла—Грейнджера. (Конспект) Шаги метода: 0. Предварительный анализ ВР: исследование стационарности и определение порядка интегрирования. Возможны следующие результаты тестирования: 1) x,y – стационарные ВР; 2) x,y – ряды с различным порядком интегрирования; 3) x,y – интегрированные ВР с одинаковым порядком. 1. Тестирование коинтегрированных ВР и оценивание долгосрочной зависимости. yt=β0+β1xt+zt
Если ВР остатков (zt) не стационарен, то xt,yt – некоинтегрированы и наоборот. Для тестирования стационарности ряда остатков используют ADF тест. 2. Оценивание параметров и тестирование адекватности модели коррекции ошибок(ECM). Оценки параметров модели
Тогда
Адекватность модели: анализ значений коэффициентов регрессии на основе t-статистики. Анализ остатков, проверка значений коэффициентов и т.д. Недостатки: неинвариантна, нет обоснованного алгоритма, существование 2х этапов. Модели бинарного выбора. Пусть имеем n переменных,наличие/отсутствие признака yi = E(εi | xi)=i E(yi | xi)= xi`β. Условное мат.ожид. приxi: E(yi | xi)=P(yi=1| xi). xβ= P(yi=1| xi), 0<= xi`β<=1. При yi=1 εi=1- xi`β, при yi=0 εi=- xi`β. Т.о. при фиксир. xi отклонение случ.ошибки принимают только 2 значения, вер-сти кот.: P{ εi=1- xi`β| xi }=P{ yi=1| xi }= xi`β P{ εi=- xi`β| xi }=P{ yi=0| xi }=1- xi`β. Соотв-но случ.величина при фиксир. xi и меет мат.ожид.: E(εi | xi)=(1- xiβ)* P(εi=1- xi`β| xi)+(-xi`β P(εi=- xi`β| xi)=0. Дисперсия D{ εi | xi }=E{ εi 2(xi)}- (E(εi | xi))2=(1- xi`β)2 xi`β+(- xi`β)(-xi`β)=-xi`β(1- xi`β). Модель бинарного выбора yi=Ф(α+ βxi)+ εi. Оценки параметров В общем случае исп-ся n переменных: yi=G(β1xi1+…+ βpxip)+ εi. Обычно в качестве ф-ции G(z) исп-ся след.ф-ции: Пробит-модель Ф(z)=1/Ö2п Логит-модель l(z)=ez/1+ez – станд. логистич.распределение. Гомпит-модель G(z)=-exp(-ez) – ф-ция станд.рспределения экстрем. значений 1-го типа. Показатели качества модели бинарного выбора: R2=RSS/TSS=1-ESS/TSS - коэф.детерминации. Рассмотрим «тривиальную модель»,кот. в качестве объясн-щей переменной вкл. единственную переменную=1,т.е.своб.член yi= βi+εi. , xi1=1
Одна из возможных характеристик, определ-щих качество подобранной модели-сравнение кол-в неправ.предсказаний, получ-но выбран.модели и по модели, в кот. в кач-ве объясн-щей переменной выступает константа(«тривиальные модели»). Если yi=1,то G(xi` Прогнозное значение Количество неправильных предсказаний по выбранной модели: nw,1=S| yi - Доля неправ.предсказаний ϑw,1=(1/n)S| yi - При этом ϑw,0= В качестве показателя качества модели можно взять R2predict=1- ϑw,1/ ϑw,0=1-S(yi - Пусть L1-max ф-ции правдоподобия для выбран.модели, L0- для тривиальной модели. При этом L0<= L1<=1. lnL0<=lnL1<=0. Pseudo R2=1-((1/1+2(lnL1- lnL0)/n). McFaddenR2=1-(lnL1/(lnL0) Цели и задачи эконометрического анализа. Классификация и основные типы моделей. Основана на 3 напрвлениях: ЭТ, Мат методы, стат теория. Цель: придание кол-ого выражения общим закон-тям ЭТ на БД стат наблюдений с исп-ния мат стат инструментария. Задачи: анализ причинно-следств связей между эк переменными; прогноз показателей в экономике; имитация разл возм сценариев соц-эк развития анализируем системы. Использование в: макроэк-ка, монетарная эк-а, межд эк-а, фин рынки, микроэкономика. Классификация данных моделей: пространств(совокупность значений полученные из некот группы n>1 объектов в фиксир момент времени), времен(упорядочен мн-во, хар-щее изменение показ-лей во времени), панельные(сочетание пространств и временных). Общий вид модели: пусть состояние некот эконом процесса или явления в момент времени t харак-ся перемен yt, следовательно, зависимая переменная(эндогенная). Состояние процесса зависит от ф-ров: 1)случайные неконтролируемые ф-ры,
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 447; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.114.166 (0.017 с.) |

 (1)
(1) ;
; 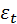 – случ ошибки соблюдения эндоген переменной.
– случ ошибки соблюдения эндоген переменной.




 c, то H0 отклоняется, и дополнительные переменные увеличивают возможности объяснения уравнений.
c, то H0 отклоняется, и дополнительные переменные увеличивают возможности объяснения уравнений. по оси х -
по оси х -  .
.




 ---- куча точек (в пунктах a,b,c – на всей площади между прямыми, в пунктах d, e – расположены около самой кривой).
---- куча точек (в пунктах a,b,c – на всей площади между прямыми, в пунктах d, e – расположены около самой кривой).
 образует авторегрессионный процесс 1-го порядка, т.е. удовлетворяет рекуррентному соотношению:
образует авторегрессионный процесс 1-го порядка, т.е. удовлетворяет рекуррентному соотношению:  (2-го порядка:
(2-го порядка:  ), где
), где  -последовательность независимых нормально распределенных случайных величин с
-последовательность независимых нормально распределенных случайных величин с 
 - некоторый параметр, называемый коэффициентом авторегрессии;
- некоторый параметр, называемый коэффициентом авторегрессии; 
 - положительная автокорреляция; иначе – отрицательная.
- положительная автокорреляция; иначе – отрицательная.



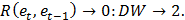

 (уровень значимости) и всей матрицы X.
(уровень значимости) и всей матрицы X. с теоретическими значениями
с теоретическими значениями  и
и  для заданных числа наблюдений
для заданных числа наблюдений  , числа независимых переменных модели
, числа независимых переменных модели  и уровня значимости
и уровня значимости  .
.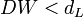 , то гипотеза о независимости случайных отклонений отвергается (следовательно, присутствует положительная автокорреляция);
, то гипотеза о независимости случайных отклонений отвергается (следовательно, присутствует положительная автокорреляция); , то гипотеза не отвергается;
, то гипотеза не отвергается; , то нет достаточных оснований для принятия решений.
, то нет достаточных оснований для принятия решений. .
.


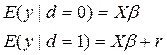
 интерпретируется как среднее изменение з/п при
интерпретируется как среднее изменение з/п при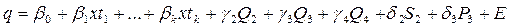
 ,
,  ,
, 
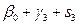 . Коэф.
. Коэф.  отражает отличив. сезон воздействия по сравнению с первым кварталам,
отражает отличив. сезон воздействия по сравнению с первым кварталам, 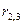 коэф. отраж. Различия в соц группах к 1-ой соц группе.
коэф. отраж. Различия в соц группах к 1-ой соц группе.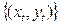 , где xt- объем инвестиций, yt – выпуск
, где xt- объем инвестиций, yt – выпуск

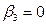 .
.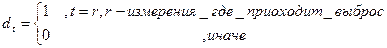

 .
. ;
; ,
,  ,
,  ;
; ;
; ;
; ,
,  , где a и b – оценки
, где a и b – оценки  и
и  .
. ,
,  , то есть, уравнение является однозначно идентифицируемым.
, то есть, уравнение является однозначно идентифицируемым. .
. (1)
(1) (2)
(2) , k – число периодов в году.
, k – число периодов в году. /
/ 
 выделяются несколько составляющих динамики:
выделяются несколько составляющих динамики: 
 , где
, где  тренд, который соответствует медленному изменению, происходящему в некотором направлении, которое сохраняется на протяжении значительного промежутка времени;
тренд, который соответствует медленному изменению, происходящему в некотором направлении, которое сохраняется на протяжении значительного промежутка времени;  сезонная компонента, отражающая изменения, происходившие в течение недели, месяца, года. Они связаны с ритмами человеческой активности (перевозка пассажиров в различные времена года);
сезонная компонента, отражающая изменения, происходившие в течение недели, месяца, года. Они связаны с ритмами человеческой активности (перевозка пассажиров в различные времена года);  циклическая компонента, отражающая повторяемость экономических процессов в течение длительных периодов. Более быстрая, нежели тенденция; присутствуют фазы возрастания и убывания;
циклическая компонента, отражающая повторяемость экономических процессов в течение длительных периодов. Более быстрая, нежели тенденция; присутствуют фазы возрастания и убывания;  случайная составляющая, которая вызвана воздействием случайных факторов, не поддающихся учету. Также среди составляющих динамики можно выделить:
случайная составляющая, которая вызвана воздействием случайных факторов, не поддающихся учету. Также среди составляющих динамики можно выделить: . t=m+4l, l=0,1,…n; r1 и r2 – номер периода начала и окончания сезонной волны; m=1,2,3,4 для квартальных данных, m=1…12 Для сезонных.
. t=m+4l, l=0,1,…n; r1 и r2 – номер периода начала и окончания сезонной волны; m=1,2,3,4 для квартальных данных, m=1…12 Для сезонных. r - номер периода тренда.
r - номер периода тренда.
 , где f(.) – детерминированная функция времени, E(
, где f(.) – детерминированная функция времени, E( )=0, D(
)=0, D( .
.
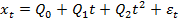

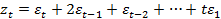
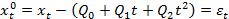
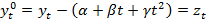


 ------нестацион.
------нестацион.
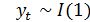

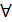
 :
:  (ряд остатков является нестационарным), то регрессия y(x) является фиктивной.
(ряд остатков является нестационарным), то регрессия y(x) является фиктивной. стац., то ряды
стац., то ряды  и
и  наз-ся коинтегрированными, а вектор (1, -b) – коинтегрирующий вектор.
наз-ся коинтегрированными, а вектор (1, -b) – коинтегрирующий вектор. такой что
такой что  . Если сущ-ет
. Если сущ-ет  , то
, то  , C=const – также коинтегрирующий вектор.
, C=const – также коинтегрирующий вектор. Если
Если  (эк. переменные) взаимосвязаны, то их изменения во времени должны быть определённым образом согласованы.
(эк. переменные) взаимосвязаны, то их изменения во времени должны быть определённым образом согласованы.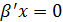 (лин-я комб-я д. б. =0),
(лин-я комб-я д. б. =0),  - вектор параметров.
- вектор параметров. ,
,  - случайная величина, обусловленная действием в момент времени t краткосрочных факторов, она называется неравновесной ошибкой.
- случайная величина, обусловленная действием в момент времени t краткосрочных факторов, она называется неравновесной ошибкой. выдвигаются следующие предположения:
выдвигаются следующие предположения: 

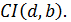
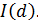
 :
:  b>0
b>0 – коинтегрирующий вектор.
– коинтегрирующий вектор. - при помощи МНК
- при помощи МНК


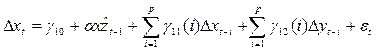
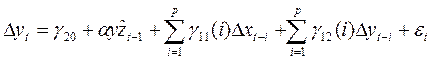
 . yi= β1xi1+…+ βpxip+ εi,где xi1,…, xip – объясняющие переменные, β1.. βp- неизв.параметры,кот.подлежат оценке, εi- случ.ошибки, отраж. влияние неизв.факторов.
. yi= β1xi1+…+ βpxip+ εi,где xi1,…, xip – объясняющие переменные, β1.. βp- неизв.параметры,кот.подлежат оценке, εi- случ.ошибки, отраж. влияние неизв.факторов. =
= 
 =1/
=1/ 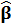 . Если применить МНК: F(α, β)=S(yi-Ф(*))=>min, но Ф нелин.по параметрам. При применении МНК к нел. ф-ции сталкиваемся с проблемой гетероскед-сти. Можно использовать взвешенную МНК: веса wi=1/D(εi | xi).Поэтому для оценивания неизв.параметров ф-ции Ф исп-ся метод максим. правдоподобия(ММП).
. Если применить МНК: F(α, β)=S(yi-Ф(*))=>min, но Ф нелин.по параметрам. При применении МНК к нел. ф-ции сталкиваемся с проблемой гетероскед-сти. Можно использовать взвешенную МНК: веса wi=1/D(εi | xi).Поэтому для оценивания неизв.параметров ф-ции Ф исп-ся метод максим. правдоподобия(ММП). dt – ф-ция чтанд.норм.распределния N(0;1)
dt – ф-ция чтанд.норм.распределния N(0;1) -ср.значение.
-ср.значение.  =
= 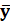 => ESS=TSS R2=0.Если в правой части добавляется новая объясняющая переменная => R2 возрастаеи, а max, если вып-ся соотношение yi= xi`β.
=> ESS=TSS R2=0.Если в правой части добавляется новая объясняющая переменная => R2 возрастаеи, а max, если вып-ся соотношение yi= xi`β.
 >1/2 или
>1/2 или 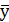 >1/2. Т.е. значения yi=1 наблюдается более, чем в половине наблюдений, а yi=0 не более чем ½ наблюдений.
>1/2. Т.е. значения yi=1 наблюдается более, чем в половине наблюдений, а yi=0 не более чем ½ наблюдений. .
. LRI-индекс отношения правдоподобия.
LRI-индекс отношения правдоподобия.


