
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нестационарные временные ряды.Содержание книги Поиск на нашем сайте
Модель AR(1)(авторегр.1-го порядка): xt=a1xt+εt стац,когда |a1|<1, если a1 изменяется от 0 до 1,1 =>белый шум. Модель xt=xt-1+εt:=случайное блуждание а=1. Представим эту модель в след.виде: xt-xt-1 =a1xt-1-xt-1-εt=(a1-1)xt-1+εt. ∆xt =φxt-1+ εt-1 φ = a1-1. Возможно 3 ситуации: 1) а1=1, φ=0 ∆xt= εt =>белый шум. 2) а1>1, φ= a1-1>0. Условное мат.ожидание при фиксиров. xt-1 :E(∆xt| xt-1)= φxt-1. Это мат.ожид.имеет тот же знак, что и xt-1 и приводит к очень быстрому удалениюот нач.значения. 3) 0<a1<1, φ= a1-1<0. E(∆xt| xt-1)= φxt-1 имеет знак,противоп. xt-1. Рассм.случай блуждания со старт.знач. х0: xt=(xt-2+ εt-1)+ εt= (xt-3+ εt-2)+εt-1=….= х0+(ε1+…+ εt) . xt= х0+ E(xt| x0)= x0. Дисперсия D(xt|x0)=D(ε1+…+ εt)=tD(εt)=td2ε => получ.ряд нестационарен. Cov(xt, xt-1)=(t-1) d2ε, Corr(xt, xt-1)= При x0=0=> xt=
Модели нестац.рядов: 1. Модель имеет вид Стац.относит-но детерминир-го тренда f(t)--- врем.ряд Интегрированные порядка k- врем.ряд Разностностац.ряды (DS)- совок.интегрир.рядов разл.порядков k=1,2…..
TS ряд: Для случ.блуждания: TS ряд: Выводы: 1. Вычитание детерминир.составляющей TS ряда приводит к стац.ряду. 2.вычитание детерминир-ой составляющей DS ряда приводит к DS ряду. 3.диф-ание (послед.разность) TS ряда приводит к TS ряду. 4.k- кратное диф-ание ряда
Проблема ложной регрессии. Коинтегрированные временные ряды. 1957-1966, показатели E C H E=-2625,5+7,13H; C=-129,3+0,35H (0,87); E=23,9 +19,9 (0,99); C=-0,86+0,49E (0,99)
R2=r2xy - парная регрессия
R2=0,68 F=305 DW=2,15 yt = Связь порожд. наличием детерминированного тренда. Рассм-м случай стохастического тренда. Если доступны стат. данные 50 – 100, то оценённые по этим моделям данные вида 1 – 100: Там где присутствует детерминированный тренд – обнаруживается ложная регрессия. Вывод: даже если временные ряды не обнаруживают явного противоречия в своём взаимодействии, то все равно может существовать ложная регрессия ввиду детермин. либо стохаст. тренда. Пример при данных 50-100: Yt=8,616+0,598xt+ H0: Вывод: Т. к. t Вопрос о ложной или действительной линейной регрессионной связи между Если да, то ряды Если переменные x и y коинтегрированны, то Нестационарность этого ряда может являться причиной больших значений статистики. Возможные варианты решения проблемы ложной регрессии. 1) Включить в правую часть уравнения лаговые значения переменных.
а) б) 2) Перед оценив. моделью продиф-ть
3) Рассмотрим модель с автокорреляционными остатками
Коинтегрированные ряды. Пусть Если для В случае когда
В эконом-й теории значит-е место занимает понятие равновесия – состояния экономической системы при котором взаимодействие разнонаправленных сил взаимопогашается таким образом, что наблюдаемые свойства системы остаются неизменными. Пусть имеется n-мерный случайный вектор x компоненты нестационарного ВР.
Если экон-й системы сущ-ет сост-е равновесия, то эти переменные должны удовлетворять определённым ограничениям:
Это тождество описывает зависимость м-ду переменными, кот-е имеют место в долгосрочной перспективе в сост-ии равновесия. В конкретный момент времени t может иметь место случайное отклонения от равновесного состояния, кот-е выр-ся следующим образом: Относительно Говорят что компоненты вектора x являются коинтегрированными порядка d,b. Обзначаются Если а) все компонентиы вектора x являются б) сущ-ет вектор
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 607; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.109.152 (0.01 с.) |

 => мат.ожид.
=> мат.ожид.
 - модель стохастич.тренда. Мат.ожид. E(xt)=, D(xt)= td2 ε
- модель стохастич.тренда. Мат.ожид. E(xt)=, D(xt)= td2 ε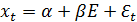 2. Модель
2. Модель  . Для удаления тренда I рода приводят к:
. Для удаления тренда I рода приводят к: 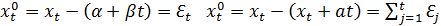 . При удалении тренда не всегда ряд приводится к стац. Привести к стац.если перейти от ур.ряда к ряду разности→процесс перехода: диф-ание. => для первого ряда:
. При удалении тренда не всегда ряд приводится к стац. Привести к стац.если перейти от ур.ряда к ряду разности→процесс перехода: диф-ание. => для первого ряда:  (MA (1)), где
(MA (1)), где  =>для второго:
=>для второго: 

 если ряд представл. собой разность между
если ряд представл. собой разность между  ; ----если ряд
; ----если ряд  явл.TS рядом 2. Ряд
явл.TS рядом 2. Ряд  получен в рез-те k-кратного диф-ния—явл.стац-ым. 3.
получен в рез-те k-кратного диф-ния—явл.стац-ым. 3. 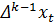 ряд при (k-1) диф-ии не явл. TS рядом.
ряд при (k-1) диф-ии не явл. TS рядом. -нестац.;
-нестац.;  ; DS ряд:
; DS ряд: 
 ; DS ряд:
; DS ряд: 
 приводит к стац.ряду.
приводит к стац.ряду.
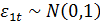 yt=2-1,04t+
yt=2-1,04t+  xt =1+0,2t+
xt =1+0,2t+  yt=
yt=  +
+  xt+
xt+  yt = 2+
yt = 2+ 
 ,
, 
 R2=0,55
R2=0,55 0
0

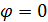 tкр=-3,46 t
tкр=-3,46 t  =-2,92
=-2,92 , то гипотеза единичного корня не отвергается, ряд остатков нестационарен.
, то гипотеза единичного корня не отвергается, ряд остатков нестационарен. , представляющих интегрированные ряды 1го порядка формируются след образом. Существует ли такое значение
, представляющих интегрированные ряды 1го порядка формируются след образом. Существует ли такое значение  стационарен.
стационарен. является оценкой того значении
является оценкой того значении 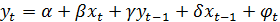



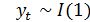

 =
= 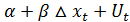




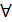
 :
:  (ряд остатков является нестационарным), то регрессия y(x) является фиктивной.
(ряд остатков является нестационарным), то регрессия y(x) является фиктивной. стац., то ряды
стац., то ряды  такой что
такой что  . Если сущ-ет
. Если сущ-ет  , то
, то  , C=const – также коинтегрирующий вектор.
, C=const – также коинтегрирующий вектор. Если
Если  (эк. переменные) взаимосвязаны, то их изменения во времени должны быть определённым образом согласованы.
(эк. переменные) взаимосвязаны, то их изменения во времени должны быть определённым образом согласованы.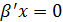 (лин-я комб-я д. б. =0),
(лин-я комб-я д. б. =0),  ,
,  - случайная величина, обусловленная действием в момент времени t краткосрочных факторов, она называется неравновесной ошибкой.
- случайная величина, обусловленная действием в момент времени t краткосрочных факторов, она называется неравновесной ошибкой. выдвигаются следующие предположения:
выдвигаются следующие предположения: 

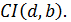
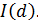
 :
:  b>0
b>0 – коинтегрирующий вектор.
– коинтегрирующий вектор.


