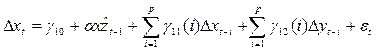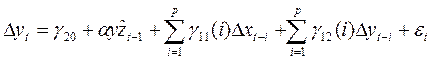Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коинтеграция модели коррекции ошибок.Содержание книги Поиск на нашем сайте Если 1 из рядов стац., а второй интегрированный 1-го порядка, то нет смысла строить модель авторегрессии.0 yt Если вектор β=(β1, β2)не=0 явл-ся коинтегрирующим вектором, то и вектор вида c=const c β=(cβ1,cβ2) тоже будет коинтегрирующим. Пусть имеется n-мерный случайный вектор x, компонетны кот. это нестацион. временные ряды Х= β`x=0 (их лин.комбинация).Это тождество описывает зависимость между переменными,кот.имеют место в долгоср.перспективе в состоянии равновесия. β`x=zt- отклонение от равнов.системы в конкр.мрмент времени t. zt-случ.величина, обусловл.действием в момент времени t краткоср. факторов – неравновесная ошибка. Относительно zt след.предположения: -E(zt)=0 -D(zt)<< b)сущ.βне=0, что zt=β`xt~I(d-b) b>0, β-коинтегр-щий вектор(вектор коинтеграции). Механизм коррекции ошибок: Пусть х-краткоср. % ставка, у-долгоср.% ставка. Мжду этими ставками сущ. Долгоср. зав-сть след.вида y- βx=0. В каждый момент времени может иметь место отклонение от равнов сост. yt-bxt= zt. Ставки изм-ся согласованно так, что их изменения направленны на восстановление равновесия путем коррекции ошибок ztв соотнош. yt-bxt= zt. В соотв. с механизмом коррекции ошибок величина и направление изменений % ствок в периоде t должны опред-ся величиной и знаком ошибки zt-1= yt-1-βxt-1, имевшим место в предыд.периоде.Для рассмотрения случая модель коррекции ошибок ECM: ∆ xt=αx(yt-1- βxt-1)+εxt, ∆yt=αy(yt-1- βxt-1)+εyt (*) αx, αy>0/ ∆ xt, ∆yt- краткоср.изменение% ставок, εxt, εyt- процессы белого шума. αx, αy, β-параметры. Соотношение (*) описывает краткоср. зав-сть между анализируемыми эеон.переменными.Если yt-1- βxt-1>0, то в след.периоде краткоср. ставки должны возрасти, а долгоср. понизиться и наоборот. Если yt-1- βxt-1<0, то коррекции ошибок нет, а изменения ∆ xt, ∆yt обусловлены только воздействием случ.факторов ε. Параметры αx, αy характеризуют скорость коректировки:чем больше αx, αy, тем больше доля отклонения от равновесия за прошлый период кор-ся в след.периоде .Условия αx, αy не=0 выполняются,если между переменными х и у сущ. Причинная зависимость по Грейнджеру. Если αхне=0, αy=0, то у не воияет по Грейнждеру на х, но х оказывает влияние на у.Если αyне=0, αх=0, то имеется одностороннее влияние по Гр. Если αx, αy=0, то между переменными отсутствует прич.зависимость и модель (*) не явл-ся моделью коррекции ошибок.Представление приращений ∆ xt, ∆yt, интегриров.времен.рядов xt и yt в виде модели ECM возможно, если врем.ряды явл-ся коинтегрированными. Предположим, что εxt и εyt- процессы белого шума, треб-щиеотсутствия автокор. для времен.рядов модели (*).=> Обобщение модели ECM: ∆ yt= γ20+ αy(yt-1- βxt-1)+ S γ21(i) ∆ xt-1+S γ22(i) ∆yt-i+yxt (**) – модель векторнойавторегрессии для 1-ых разностей.Модели ∆ xt, ∆yt- векторные модели коррекции ошибок. Построение ECM с помошью подхода Энгла-Грейнджера: 1. предварит.анализ врем.рядов:исслед.стационарности и опрделение порядка интегриров-сти для врем.рядов, кот. будут исп-ны для постр.модели ECM.Возможны след.ре-ты тестирования: - х и у стац.врем.ряды -х и у ряды интегрир. С разным порядком интегрир. -х и у интегр.врем.ряды с один.порфдком интегрируемости. 2. тестирование коинтегрир-сти врм.рядов с оцениванием долгоср.зав-сти yt=β0+ β1xt+zt/ С пом.МНК нах-ся β0 и β1.вычисл-ся ряд остатков 3. Оценивание параметров и тестирвание адекватности модели коррекции ошибок. Находятся оценки параметров модели вида (**).
Подход Энгла—Грейнджера Простейшим методом отыскания стационарной линейной комбинации является метод Энгла—Грейнджера. Энгл и Грейнджер предложили использовать оценки, полученные из обычной регрессии с помощью метода наименьших квадратов. Одна из переменных должна стоять в левой части регрессии, другая—в правой: y t = β0+ β1xt + zt. Для того чтобы выяснить, стационарна ли полученная линейная комбинация, предлагается применить метод Дики—Фуллера к остаткам из коинтеграционной регрессии. Нулевая гипотеза состоит в том, что zt содержит единичный корень, т.е. y t и xt не коинтегрированы. Пусть zt —остатки из этой регрессии. Статистика Энгла—Грейнджера представляет собой обычную t -статистику для проверки гипотезы ϕ = 1 в этой вспомогательной регрессии. Распределение статистики Энгла—Грейнджера будет отличаться (даже асимптотически), от распределения DF-статистики, но имеются соответствующие таблицы. Если мы отклоняем гипотезу об отсутствии коинтеграции, то это дает уверенность в том, что полученные результаты не являются ложной регрессией. Игнорирование детерминированных компонент ведет к неверным выводам о коинтеграции. Чтобы этого избежать, в коинтеграционную регрессию следует добавить соответствующие переменные — константу, тренд, квадрат тренда, сезонные фиктивные переменные. Такое добавление, как и в случае критерия DF, меняет асимптотическое распределение критерия Энгла—Грейнджера. (Конспект) Шаги метода: 0. Предварительный анализ ВР: исследование стационарности и определение порядка интегрирования. Возможны следующие результаты тестирования: 1) x,y – стационарные ВР; 2) x,y – ряды с различным порядком интегрирования; 3) x,y – интегрированные ВР с одинаковым порядком. 1. Тестирование коинтегрированных ВР и оценивание долгосрочной зависимости. yt=β0+β1xt+zt
Если ВР остатков (zt) не стационарен, то xt,yt – некоинтегрированы и наоборот. Для тестирования стационарности ряда остатков используют ADF тест. 2. Оценивание параметров и тестирование адекватности модели коррекции ошибок(ECM). Оценки параметров модели
Тогда
Адекватность модели: анализ значений коэффициентов регрессии на основе t-статистики. Анализ остатков, проверка значений коэффициентов и т.д. Недостатки: неинвариантна, нет обоснованного алгоритма, существование 2х этапов.
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 785; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 I(1), xt
I(1), xt  . Если эти переменные x1t,….,xnt взаимосвязаны, то их изменения во времени должны быть опред.образом согласованны, т.е. траектории этих рядов не отдаляются далеко друг от друга. Если для эк.системы сущ. равновесие(состояние эк.системы, при кот.воздействие разнонапр.сил взаимно погашается таким образом, что наблюдаемые св-ва системы ост-ся неизменными), то переменные x1t,….,xnt должны удовлетворять опред. ограничениям.
. Если эти переменные x1t,….,xnt взаимосвязаны, то их изменения во времени должны быть опред.образом согласованны, т.е. траектории этих рядов не отдаляются далеко друг от друга. Если для эк.системы сущ. равновесие(состояние эк.системы, при кот.воздействие разнонапр.сил взаимно погашается таким образом, что наблюдаемые св-ва системы ост-ся неизменными), то переменные x1t,….,xnt должны удовлетворять опред. ограничениям.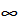 . Говорят,что компоненты вектора х явл-ся коинтегриров.порядка d и b и обозн-ся CI(d,b), если а) все компоненты вектора х явл-ся интегр.порядка d
. Говорят,что компоненты вектора х явл-ся коинтегриров.порядка d и b и обозн-ся CI(d,b), если а) все компоненты вектора х явл-ся интегр.порядка d t= yt-
t= yt-  0-
0-  I(0)-коинтегр. Для тестирования стационарности ряяда остатков тест Дикки-Фуллера.
I(0)-коинтегр. Для тестирования стационарности ряяда остатков тест Дикки-Фуллера. - при помощи МНК
- при помощи МНК