
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система одновременных уравненийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
— совокупность эконометрических уравнений (часто линейных), определяющих взаимозависимость экономических переменных. Важным отличительным признаком системы «одновременных» уравнений от прочих систем уравнений заключается в наличии одних и тех же переменных в правых и левых частях разных уравнений системы (речь идет о так называемой структурной форме модели). Эндогенными называются переменные, значения которых определяются в процессе функционирования изучаемой экономической системы. Их значения определяются «одновременно» исходя из значений некоторых экзогенных переменных, значения которых определяются вне модели, задаются извне. В системах одновременных уравнений эндогенные переменные зависят как от экзогенных переменных, так и от эндогенных. Измерение тесноты связи между переменными, построение изолированных уравнений регрессии недостаточно для объяснения функционирования сложных экономических систем. Изменение одной переменной не может происходить при абсолютной неизменности других. Её изменение повлечет за собой изменения во всей системе взаимосвязанных признаков. Таким образом отдельно взятое уравнение регрессии не может характеризовать истинное влияние отдельных признаков на вариацию результирующей переменной. Поэтому в экономических исследованиях важное место заняла проблема описания структуры связей между системой переменных. Структурной формой системы называется представление системы, в котором в уравнениях может присутствовать более одной эндогенной переменной (в стандартной записи это означает, что в правой части уравнений, то есть в качестве регрессоров, имеются эндогенные переменные). Структурная форма системы описывает систему взаимозависимостей между экономическими переменными.
Перенеся эндогенные переменные в левую часть структурную форму можно представить в следующем матричном виде Приведённой (прогнозной) формой системы называется представление системы, в котором в каждом уравнении имеется только одна эндогенная переменная, то есть эндогенные переменные выражены через экзогенные: Это так называемая неограниченная приведённая форма. Структурную форму можно записать следующим образом: Это так называемая ограниченная приведённая форма, то есть приведённая форма с ограничением на коэффициенты следующего вида: Если задана структурная форма, то всегда можно получить ограниченную приведённую форму (предполагается, что матрица А невырождена). Однако, обратное не всегда возможно, а если возможно, то не всегда однозначно.
18. Проблема идентификации систем одновременных уравнений (СОУ). Проблема оценивания параметров и возможности преобразования структурной формы к приведённой тесно связана с понятием идентификации модели. Исходную систему уравнений называют идентифицируемой (точно определенной), если по коэффициентам приведённой формы уравнений можно однозначно определить значения коэффициентов структурной формы уравнений. Исходную систему называют неидентифицируемой (недоопределенной), если по коэффициентам приведённой формы уравнений невозможно определить значения всех коэффициентов структурной формы уравнений. В этом случае система, связывающая коэффициенты структурной и приведённой форм несовместна. Исходную систему уравнений называют сверхидентифицируемой (переопределенной), если по коэффициентам приведённой формы уравнений можно получить несколько значений коэффициентов структурной формы уравнений. Для оценки параметров СОУ используются косвенный и двухшаговый МНК (подробно в 19-м вопросе). Для быстрого формального определения идентифицируемости структурной формы уравнения применяются следующие необходимые условия: СОУ включает в себя N уравнений относительно N эндогенных переменных. Пусть в системе M предопределенных (экзогенных) переменных, а число эндогенных (зависимых) и экзогенных (предопределённых) переменных в проверяемом уравнении n и m соответственно. Разница M-m – число предопределённых переменных, не включённых в проверяемое уравнение, но присутствующее в системе. Тогда существует 3 случая: - если M-m > n-1, то уравнение сверхидентифицируемо; - если M-m = n-1, то уравнение идентифицируемо; - если M-m < n-1, то уравнение неидентифицируемо. Пример. Модель совокупного спроса и предложения
В первом уравнении 2 эндогенные переменные Во втором уравнении 2 эндогенные переменные и нет экзогенных переменных. Т. е. выполняется M-m = n-1 (1-0=2-10), т. е. уравнение идентифицируемо. Оценивание СОУ. Косвенный Метод Наименьших Квадратов (КМНК) – один из способов решения СОУ. Он включает последовательность шагов: 1.Исходя из структурных уравнений строятся уравнения приведённой формы. 2. С помощью МНК оцениваются параметры уравнений приведённой формы. 3. На основе полученных оценок находятся параметры структурных уравнений. Рассмотрим КМНК на примере модели: Пример для случая идентифицируемости. Запишем приведённую форму:
C помощью МНК находим оценки неизвестных параметров a’ и b’:
В результате получаем:
Подробнее о случаях идентифицируемости, неидентифицируемости и сверхидентифицируемости смотрите в 18-м вопросе. Двухшаговый МНК (ДМНК) применяется в тех случаях, когда уравнение сверхидентифицируемо. Алгоритм: 1. Составляется приведённая форма модели и определяются численные значения параметров с помощью МНК. 2. Рассматриваются теоретические знания эндогенных переменных. 3. Обычным МНК определяются параметры структурного уравнения, используя в качестве исходных данных расчётные значения предопределённых переменных, стоящих в правой части уравнения. Замечание. Если условие идентифицируемости для уравнения выполнено со знаком равенства, то оценка, полученная с помощью ДМНК, совпадает с оценкой, полученной с помощью КМНК.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 791; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.73.107 (0.006 с.) |





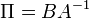 .
.
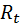 и
и  (n=2) и 1 экзогенная
(n=2) и 1 экзогенная 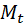 (m=1). Всего в системе 1 экзогенная переменная
(m=1). Всего в системе 1 экзогенная переменная  .
. ;
; ,
,  ,
,  ;
; ;
; ;
; ,
,  , где a и b – оценки
, где a и b – оценки  и
и  .
. ,
,  , то есть, уравнение является однозначно идентифицируемым.
, то есть, уравнение является однозначно идентифицируемым.


