
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретно-непрерывная системаСодержание книги
Поиск на нашем сайте
W (z) = Z{ W 1(s) W 2(s)… Wn (s)} = W 1 W 2 W 3… Wn (z)
Правило: Дискретная передаточная функция последовательного соединения непрерывных звеньев не равна произведению их Z -форм, а равна Z -форме произведения их непрерывных передаточных функций. Дискретная система с несколькими импульсными Элементами
W (z) = W 1(z) W 2(z), где W 1(z) = Z { W 1(s)}, W 2(z) = Z { W 2(s)}. Правило: Передаточная функция нескольких последовательно соединенных непрерывных звеньев, разделенных импульсными элементами, равна произведению их Z -форм от непрерывных передаточных функций. Дискретно-непрерывная система W (z) =
Правило: Дискретная передаточная функция параллельного соединения непрерывных звеньев равна сумме дискретных передаточных функций отдельных ветвей.
Дискретная система с несколькими импульсными
элементами Правило: Параллельные каналы с безинерционными звеньями и импульсными элементами, работающими синхронно и с одинаковым периодом квантования, могут быть заменены одним импульсным элементом, включенным после узла суммирования. Дискретно-непрерывная система с единичной обратной связью
     X (s) E (s) Y (s) X (s) E (s) Y (s)
Y (z, Y (z, Положим Y (z) = W (z) X (z) - W (z) Y (z) = Подставляя в уравнение для Y (z, Y (z, Передаточная функция замкнутой системы по управлению: Фx (z, Получим передаточную функцию замкнутой системы по ошибке: Фе (z, где E (z, К сожалению, из полученного выражения E (z, Фе (z) = Отметим, что по форме передаточные функции замкнутой дискретно-непрерывной системы полностью совпадают с соответствующими передаточными функциями непрерывной системы.
Дискретные системы произвольной структуры
Под произвольной структурой мы будем понимать расположение одного или нескольких импульсных элементов в различных местах дискретной системы, (в прямом канале, в канале обратной связи, между непрерывными звеньями и т.д.). Для записи уравнений или передаточных функций в таких системах следует использовать три основных правила записи уравнений в Z-изображениях.
*Правило1: Z-изображение выходного сигнала одного или нескольких последовательно соединенных непрерывных звеньев, подвергнутых воздействию дискретного сигнала, равно произведению Z-изображения, входного сигнала на Z-преобразование непрерывной передаточной функции. Рисунок ниже иллюстрирует это правило:
Правило2: Если одно или группа непрерывных последовательно соединенных звеньев подвергнута воздействию непрерывного сигнала, то Z-изображение выходного сигнала равно Z-преобразованию произведению изображения входного сигнала на непрерывные передаточные функции звеньев.
Y (z) = Z { X (s)} W (s)} = XW (z). Y (z) = Z { X (s)} W 1(s) W 2(s)} = XW 1 W 2(z) Y (z,
Правило 3. Z – изображение выходного сигнала группы звеньев, разделенных импульсными элементами, работающими синхронно и с одинаковым периодом квантования, равно произведению Z-форм передаточных функций отдельных звеньев.
Y (z) = X (z) W 1(z) W 2(z) W 3(z), где W 1(z) = Z { W 1(s)}; W 2(z) = Z { W 2(s)}; W 3(z) = Выражение Y (z,
Пример: Простая система с одним импульсным элементом и неединичной обратной связью. Для записи выражения передаточных функций системы по управлению G (s) и ошибке E (s) разорвем искусственно систему (разрыв всегда делается перед импульсным элементом или перед первым импульсным элементом, если их несколько).
E (s) E (s)
Запишем выражение для E (z) E (z) = - E (z) W 1 W 2(z) + G (z) = G (z) Передаточная функция замкнутой системы по управлению Фg (z)= Передаточная функция замкнутой системы по ошибке: Фe (z) = Непосредственное применение правила Мэйсона к графу, эквивалентному структурной схеме дискретно-непрерывной системы, невозможно. Существует два пути использования правила Мэйсона для дискретно-непрерывных систем:
1) составление дискретного графа, в котором все переменные представлены дискретными величинами и для которого применение правила Мэйсона допустимо; 2) использования исходного эквивалентного графа с изменением формулы Мэйсона. Первый путь является более простым и эффективным и поэтому получил широкое распространение в практике анализа дискретно-непрерывных систем, особенно при решении задачи записи уравнений в Z-изображениях для систем сложной структуры с несколькими дискретными элементами. В качестве иллюстрации использования формулы Мэйсона и записи уравнений в Z-изображениях рассмотрим простую дискретную систему с одним дискретным элементом и неединичной отрицательной обратной связью (рис. 2.23), использованную выше для составления эквивалентного графа. Уравнения для входа и выхода в изображениях E (s) = G (s) - W (s) W ос(s) E *(s), Y (s) = W (s) E *(s). Подвергнем Z-преобразованию записанные уравнения E (z) = G (z) - WW ос(z) E (z) = Составляем дискретный граф системы
- WW ос(z) К такому графу правило Мэйсона применяется без всяких ограничений и условий:
Передачи между непрерывными и дискретными сигналами могут быть определены из так называемого составного графа. Составным графом называется совокупность дискретного и эквивалентного графов, полученная путем соединения выходных узлов квантователей эквивалентного графа с аналогичными узлами дискретно графа дугами с единичными передачами.
- WW ос(z) 1 E (z) W 1(s) G (s) E (s) Y (s)
- Wx (s)
Составной граф для рассматриваемой нами системы будет следующим: Применение правила Мэйсона к составному графу позволяет записать выражения передач для всех непрерывных и дискретных вершин. Так например,
Векторно-матричное описание
При переходе к дискретной аппроксимации непрерывной части системы будем считать, что входной сигнал квантуется с периодом Т, а затем преобразуется экстраполятором нулевого порядка. Это значит, что внешнее воздействия U (t) остается постоянным в течение n -такта квантования, т. е. U (t) = u (nT), при nT Известно, что решением основного векторно-матричного уравнения непрерывной системы X (t) = Ф (t) X (o) + где Ф (t)= eAt - переходная матрица системы, имеющая форму матричной экспоненты eAt. Она вычисляется либо как сумма степенного ряда eAt = I + Используем выражение (5.1) для определения вектора состояния во времени интервала nT Введем обозначения: A * = Ф (T); B *=[ X (n + 1) = A * X (n) + B * U (n), Y (n) = CX (n) + DU (n). По форме полученные уравнения являются полной аналогией векторно-матричных уравнений непрерывной системы. Векторно-матричное описание дискретной системы Пусть дискретная система описывается передаточной функцией W (z) =
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 412; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.253.217 (0.009 с.) |



 , где Wi (z) = Z { Wi (s)}
, где Wi (z) = Z { Wi (s)}



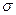 ) = W (z,
) = W (z,  .
. X (z)] =
X (z)] =  X (z).
X (z). =
=  ,
, =0, тогда
=0, тогда  X (z). Тогда передаточная функция замкнутой системы по ошибке при
X (z). Тогда передаточная функция замкнутой системы по ошибке при  =
= 



 X (s) Y (s) X (s) Y (s)
X (s) Y (s) X (s) Y (s) { X (s) W (s)} = XW (z,
{ X (s) W (s)} = XW (z, 
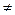 0 довольно сложное и здесь не производится.
0 довольно сложное и здесь не производится.
 Y (s) G (s)
Y (s) G (s) .
. =
=  .
. =
=  .
. , Y (z) = W (z) E (z) = G (z)
, Y (z) = W (z) E (z) = G (z)  .
.




 G (z) 1 E (z) W (z) y (z)
G (z) 1 E (z) W (z) y (z)

 .
. G (z) 1 E (z) W (z) Y (z)
G (z) 1 E (z) W (z) Y (z)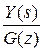 =
= 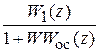 ; E (s) = G (s) -
; E (s) = G (s) -  G (z).
G (z). t
t  =AX+BU является следующее выражение
=AX+BU является следующее выражение , (5.1)
, (5.1) +…+
+…+  +…, либо как обратные преобразования Лапласа eAt =
+…, либо как обратные преобразования Лапласа eAt =  . Для момента времени t = (n + 1)T имеем X [(n + 1) T ] = Ф (T) X (nT) + U (nT)
. Для момента времени t = (n + 1)T имеем X [(n + 1) T ] = Ф (T) X (nT) + U (nT)  , или после преобразований X (n + 1) = Ф (T) X (n) + … + U (n)
, или после преобразований X (n + 1) = Ф (T) X (n) + … + U (n)  , где Ф (T) = eAT = L -1{(SI - A)-1} - - переходная матрица непрерывной части системы при t = T.
, где Ф (T) = eAT = L -1{(SI - A)-1} - - переходная матрица непрерывной части системы при t = T. ] B. Тогда векторно-матричное описание дискретной системы будет иметь вид:
] B. Тогда векторно-матричное описание дискретной системы будет иметь вид: =
=  .
.


