
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторно-матричное описание непрерывной системыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Обобщая записанную в примере систему уравнений состояния, запишем ее для системы порядка n.
…………………………………………………….
Эту систему можно записать в векторно-матричной форме:
где X = X (t) – действительный n -мерный вектор-столбец, компоненты которого переменные состояния. Поэтому он носит название вектора состояния. U = u (t) - действительный m -мерный вектор-столбец, содержащий в качестве своих элементов входные внешние воздействия (управляющие и возмущающие), он называется вектором входа. А – матрица коэффициентов системы размерностью (n x n), называемая матрицей системы или матрицей состояния. B – матрица коэффициентов системы при внешних воздействиях и поэтому называемая матрицей входа; размерность матрицы B – (n x m). Если матрицы А и В постоянные, то система называется стационарной; если матрицы А и В есть функции времени, то система называется нестационарной или системой с переменными коэффициентами. Основное матричное уравнение (3.7.) обычно дополняется уравнением для вектора выходных переменных: Y = CX + DU, (3.8.) где C – матрица выхода системы, размерность которой зависит от размерности векторов X и Y; в одномерной системе, где y есть скалярная переменная, матрица С есть строка размерностью n; D – матрица связи с внешними воздействиями, ее размерность определяется размерностью векторов U и Y. Для матричной формы описания в пространстве состояний часто используется структурное изображение, причем в матричных структурных схемах сигналы, описываемые векторами, представляются двойными стрелками. Так уравнению (3.7.) соответствует структурная схема (рис. 3.17, а), а схема, соответствующая уравнениям (3.7.) и (3.8.) совместно, показана на рис. 3.17, б.
а) б) Рис. 3.17
U x Y U y y
а) Рис. 3.18 б)
Для одномерной системы управления сигналы U, f и y являются скалярными величинами. Поэтому структурная схема одномерной системы будет иметь вид (рис.3.18, б). Здесь Bu и Bf вектор-столбцы, а матрица С вектор-строка.
Уравнения состояния непрерывной части системы:
Матрица системы: A = Определяем переходную матрицу Ф (t) = L -1{(SI - A)-1}.
0 s
L -1{
L -1{
3.5.3. Преобразование Лапласа матричного уравнения Системы управления Возьмем основное матричное уравнение системы: Рассмотрим сначала однородное матричное уравнение системы при U (t) = 0.
Объединяя члены, содержащие изображение вектора X (s), получим SX (s) – AX (s) = X (0) или (SI – A) X (s) = X (0), откуда X (s) = (SI – A)-1 X (0), где I –единичная матрица. Матрица (SI – A)-1 называется резольвентой матрицы А. Она определяется следующим образом: (SI - A)-1= Здесь det(SI – A) – определитель матрицы (SI – A); Adij (SI – A) T – квадратная матрица, элементами которой являются алгебраические дополнения элементов Aij матрицы (SI – A) T; Adji (SI – A) – матрица, элементами которой являются алгебраические дополнения элементов Aji матрицы (SI – A). Матрица (SI–A) называется характеристической. Ее определитель det(SI – Рассмотрим неоднородное матричное уравнение системы SX(s) = AX(s) + bU(s), X(s) = (SI – A)-1BU(s), Y(s) = C(SI – A)-1BU(s) = H(s)U(s), где H(s) = C(SI – A)-1B называется матричной передаточной функцией системы. Она вычисляется следующим образом: H(s)= Отметим, что знаменатель H(s) это характеристический полином D(s), что корни характеристического уравнения D(s)=0 являются одновременно полюсами передаточной функции системы H(s).
|
|||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 549; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |

 = a 11 x 1 + a 12 x 2 +…+ a 1 n xn + b 11 u 1 + b 12 u 2 +…+ b 1 m um,
= a 11 x 1 + a 12 x 2 +…+ a 1 n xn + b 11 u 1 + b 12 u 2 +…+ b 1 m um, = a 21 x 1 + a 22 x 2 +…+ a 2 n xn + b 21 u 1 + b 22 u 2 +…+ b 2 m um,
= a 21 x 1 + a 22 x 2 +…+ a 2 n xn + b 21 u 1 + b 22 u 2 +…+ b 2 m um, = ai 1 x 1 + ai 2 x 2 +…+ ainxn + bi 1 u 1+ bbi 2 u 2 +…+ bimum,
= ai 1 x 1 + ai 2 x 2 +…+ ainxn + bi 1 u 1+ bbi 2 u 2 +…+ bimum, = an 1 x 1 + an 2 x 2 +…+ annxn + bn 1 u 1 + bn 2 u 2 +…+ bnnum.
= an 1 x 1 + an 2 x 2 +…+ annxn + bn 1 u 1 + bn 2 u 2 +…+ bnnum. = AX + BU, (3.7)
= AX + BU, (3.7)

 Векторная связь через матрицу D редко встречается в обычных линейных системах с постоянными коэффициентами. Гораздо чаще используется структура с разделением управляющих и возмущающих внешних воздействий. В этом случае матрица В разделяется на две: Bu и Bf, и структурная схема приобретает вид, показанный на рис. 3.18, а.
Векторная связь через матрицу D редко встречается в обычных линейных системах с постоянными коэффициентами. Гораздо чаще используется структура с разделением управляющих и возмущающих внешних воздействий. В этом случае матрица В разделяется на две: Bu и Bf, и структурная схема приобретает вид, показанный на рис. 3.18, а. F f
F f
 ,
,  .
.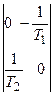 . Матрица входа В =
. Матрица входа В =  , матрица выхода C = [0 1].
, матрица выхода C = [0 1].






 SI - A = s 0 – 0 -
SI - A = s 0 – 0 -  = s
= s 
 0 -
0 - 
 (SI - A)1=
(SI - A)1=  =
=  .
. } = cos
} = cos  ; L -1{
; L -1{  } =
} =  ;
; }=-
}=-  . Таким образом, дискретная матрица системы:
. Таким образом, дискретная матрица системы:
 A * = Ф (T) =
A * = Ф (T) = 
 .
. . Подвергнем его преобразованию Лапласа с учетом начальных условий, т.е. наличия вектора X (0) SX (s) – X (0) = AX (s).
. Подвергнем его преобразованию Лапласа с учетом начальных условий, т.е. наличия вектора X (0) SX (s) – X (0) = AX (s).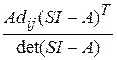 =
= 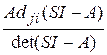 .
.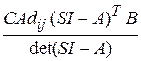 .
.


