
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ей соответствует разностное уравнениеСодержание книги
Поиск на нашем сайте a 0 y (n + q) + a 1 y (n + q - 1) +…+ aqy (n) = b 0 u (n + q) + b 1 u (n + q - 1) +…+ bqu (n). Переменные состояния примем следующие: X 1(n) = y (n); X 2(n) = x 1(n + 1) = y (n + 1); X 3(n) = x 2(n + 1) = y (n + 2); ……………………………… Xq (n) = xq -1(n + 1) = y (n + q - 1); Xq (n + 1) = y (n + q). Подставим их в разностное уравнение, приняв a 0 = 1, bq = 1, b 0 = b 1 =
Совместно с уравнением выхода Y (n)=[10…0] Вводя обозначения: X – вектор переменных состояния; А - матрица системы; В – матрица входа; С –матрица выхода; - записываем векторно-матричное уравнение дискретной системы в комплексной форме: X (n + 1) = AX (n) + BU (n); Y (n) = CX (n). Можно получить выражения матриц A,B и С и в более общем случае, когда bq Решение дискретного уравнения состояния с помощью Z-преобразования
Рассмотрим дискретное уравнение состояния X (n +1)= A * X (n)+ B * U (n), где Z – преобразование A (kT) определяется общей формулой Z –преобразования A (z) = = Вычисляя обратное Z – преобразование, получим A (kT) = Z -1{(zI - A)-1 z }. Это выражение и является основой способа определения переходной матрицы состояния, основанного на Z – преобразовании. Второе слагаемое в выражении для X(n) вычисляем с помощью теоремы свертки и выражение для A (kT); Z -1{(zI - A *)-1 B * U (z)} = Полное переходное уравнение состояния X (n) = A (n) X (0) +
Переходной характеристикой полностью дискретной системы называется реакция дискретной системы на единичную дискретную ступенчатую функцию. Графическое представление входного сигнала и математическое описание дискретной ступенчатой функции имеет вид: g и*(n) = 1, n Z – преобразование дискретного входного сигнала G и(z) =
g *и
0 1 2 3 4 5 6 n
Частотные характеристики
Построение ЛАФЧХ дискретных систем и отдельных звеньев имеет свои характерные особенности. Они следуют из того факта, что выражения модуля и фазы КПФ дискретной системы являются функциями ej w T и не логарифмируются непосредственно. Кроме того, диапазон частот дискретных характеристик
Используя формулу Эйлера ej a = cosa + j sina, имеем
Окончательно имеем
Это значит, что характеристики дискретных систем в области низких частот будут совпадать с характеристиками приведенной непрерывной части. Посмотрим, как строятся ЛАФЧХ дискретных рассмотренных выше динамических звеньев: интегрирующего и апериодического 1-го порядка. В ПФ дискретного интегратора
Далее принимаем w = j (T /2)l и получаем
Выражение ЛАЧХ
Выражение ЛФЧХ j(l) = - arctg(T /2)l - p/2. Графики ЛАФЧХ интегрирующего звена показаны на рис. 5.10.
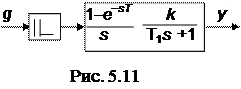
Из графиков видно, что в области низких частот ЛАФЧХ дискретного интегратора совпадают с ЛАФЧХ непрерывного интегрирующего звена (наклоном –20 дБ/дек, фазовый сдвиг j = -p/2. Существенное отличие характеристик имеет место в области высоких частот (нулевой наклон и фазовый сдвиг j = - p). Перейдем к апериодическому звену 1-го порядка. Эквивалентная схема дискретного апериодического звена имеет вид (рис. 5.11).
Тогда
Переходим к w -преобразованию Wa (z):
где
Можно доказать, что Переходя к ЛАФЧХ, получим
ja(l) = - arctg(T /2)l - arctg T 1l.
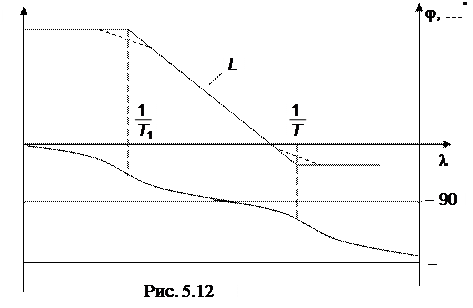
Графики L а(l) и ja(l) показаны на рис. 5.12. Как и для интегрирующего звена, так и для апериодического звена 1-го порядка наблюдается совпадение ЛАФЧХ в области низких частот и существенное различие в области высоких частот для непрерывного и дискретного режимов работы. Аналогично описанному выше строятся ЛАФЧХ других дискретных звеньев и систем. Свойство совпадения ЛАФЧХ в области низких частот сохраняет свою силу и для других более сложных звеньев и систем, что позволяет использовать для дискретных систем методы анализа и синтеза, разработанные для непрерывных систем. Отметим, что для сложной передаточной функции непрерывной части дискретно-непрерывной системы построение ЛАФЧХ может быть выполнено приближенным способом, допускающим полное совпадение характеристик непрерывной и дискретной системы в области низких частот
Устойчивость систем
Для устойчивости замкнутой дискретной системы необходимо и достаточно, чтобы при изменении частоты в диапазоне 0 £ w £ p/ T годограф характеристического полинома обошел в положительном направлении 2 n квадрантов, нигде не обращаясь в нуль и не пересекаясь сам с собой. Годографы устойчивых дискретных систем второго и четвертого порядка показаны на рис. 5.13.
 Как и отмечалось ранее, крайние точки годографов D (ej 0) и D (ej p) являются вещественными и находятся на вещественной оси. Как и отмечалось ранее, крайние точки годографов D (ej 0) и D (ej p) являются вещественными и находятся на вещественной оси.
В качестве примера построим годограф для дискретного интегрирующего звена в системе с отрицательной обратной связью (рис. 5.14). Передаточная функция разомкнутой системы
Передаточная функция замкнутой системы
Характеристический полином замкнутой системы
где a 0 = 1; a 1 = kT – 1. Полагаем z = ej w T при 0 £ w £ p/ T. D (ej w T) = a 0 ej w T + a 1. График D (ej w T) показан на рис. 5.15. Он представляет собой полуокружность радиуса a 0 = 1 и с центром в точке a 1 = kT – 1.
Анализ качества Перейдем к дискретно-непрерывной системе и покажем, как определяются коэффициенты ошибок на примере типовой одноконтурной системы с одним дискретным элементом. Как и для непрерывной системы рассмотрим установившиеся ошибки при отработке трех типовых воздействий: g (t) = g 01(t), g (t) = g0t1 (t), 1. Внешнее воздействие g ( t ) = g 01( t ). Его Z -изображение Z-изображение ошибки Установившееся значение ошибки
Пусть С 0 – коэффициент ошибки по положению. Он определяется таким же, как и для непрерывной системы, выражением. Из выражения для ошибки видно, что чтобы С (¥) = 0, коэффициент передачи должен быть бесконечным. Это будет иметь место, если W 1 W 2(z) содержат хотя бы один полюс z = 1. Например, в составе W 1 W 2(z) имеется передаточная функция дискретного интегратора 2. Внешнее воздействие g (t) = g0t1 (t), Изображение ошибки
Установившиеся значение ошибки
Определим коэффициент ошибки по скорости как
где 3. Внешнее воздействие g (t) = g0t 2 1 (t), Изображение ошибки Установившееся значение ошибки
где Из выражения Замечание. Полученные выражения C 1 и C 2 справедливы только тогда, когда внешние сигналы g (t) представляют собой скачки скорости и ускорения соответственно.
Вопросы для самопроверки 1. Сформулируйте определение дискретных систем. Какова структура и классификация импульсных систем? 2. Расскажите о математическом аппарате исследования импульсных систем. 3. Сформулируйте теорему Котельникова-Шеннона. Поясните ее физический смысл и практическое значение при проектировании дискретных систем. 4. Поясните методы определения передаточных функций импульсных систем. Каковы особенности передаточных функций статических и астатических систем? 5. Каким образом определяются частотные характеристики импульсных систем? 6. Какими способами определяются переходные процессы в дискретных системах? 7. Сформулируйте условия устойчивости импульсных систем. 8. Каким образом оценивается точность работы импульсных систем? 9. Каков порядок синтеза цифровых систем? Перечислите методы определения передаточных функций корректирующих устройств. Укажите виды структурных схем цифровых фильтров.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 392; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.01 с.) |

 Полученные уравнения можно представить в виде векторно-матричного уравнения состояний:
Полученные уравнения можно представить в виде векторно-матричного уравнения состояний:
 =
= 
 +
+ 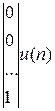
 .
.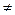 1 и b 0
1 и b 0  bq -1
bq -1  ] B. Подвергнем обе части уравнения состояния Z-преобразованию zX (z) - zX (0) = A * X (z) + B * U (z). Отсюда X (z) = (zI - A *)-1 zX (0) + (zI - A *)-1 B * u (z). Подвергая обратному Z- преобразованию, имеем X (n) = Z -1{(zI - A *)-1 z } X (0) + Z -1{(zI - A *)-1 B * u (z)}. Покажем, что обратное Z – преобразование от (zI - A *)-1 есть дискретная переходная матрица состояния A (kT).
] B. Подвергнем обе части уравнения состояния Z-преобразованию zX (z) - zX (0) = A * X (z) + B * U (z). Отсюда X (z) = (zI - A *)-1 zX (0) + (zI - A *)-1 B * u (z). Подвергая обратному Z- преобразованию, имеем X (n) = Z -1{(zI - A *)-1 z } X (0) + Z -1{(zI - A *)-1 B * u (z)}. Покажем, что обратное Z – преобразование от (zI - A *)-1 есть дискретная переходная матрица состояния A (kT). . Умножим обе части последнего уравнения на A * z -1 и вычтем результат из последнего уравнения. Получим (I - A * z -1) A (z) = I, откуда A (z) = (I - A * z -1)-1 = (zI - A *)-1 z.
. Умножим обе части последнего уравнения на A * z -1 и вычтем результат из последнего уравнения. Получим (I - A * z -1) A (z) = I, откуда A (z) = (I - A * z -1)-1 = (zI - A *)-1 z.
 .
. 0; g и*(n) = 0, n < 0.
0; g и*(n) = 0, n < 0. .
. Z – преобразование переходной характеристики H (z) = D (z) G и(z) =
Z – преобразование переходной характеристики H (z) = D (z) G и(z) =  . Эта подстановка называется w -преобразованием. Чтобы выяснить, как новая переменная w связана с обычной частотой w, используем связь z = ej w T. Из формулы w -преобразования определяем
. Эта подстановка называется w -преобразованием. Чтобы выяснить, как новая переменная w связана с обычной частотой w, используем связь z = ej w T. Из формулы w -преобразования определяем .
.

 .
.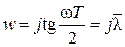 , где
, где  так называемая относительная псевдочастота. Нетрудно заметить, что при 0 £ w £ p/ T относительная псевдочастота будет меняться в диапазоне 0 £
так называемая относительная псевдочастота. Нетрудно заметить, что при 0 £ w £ p/ T относительная псевдочастота будет меняться в диапазоне 0 £  £ ¥, т. е. Частотные характеристики дискретных систем, построенные в функции
£ ¥, т. е. Частотные характеристики дискретных систем, построенные в функции  , а
, а  .
.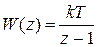 вводим подстановку
вводим подстановку  .
. .
.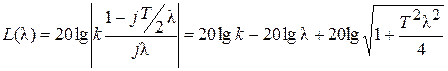 .
.
 Дискретная передаточная функция апериодического звена
Дискретная передаточная функция апериодического звена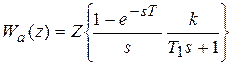 =
= . Для определения
. Для определения  предварительно разложим
предварительно разложим  на сумму простых слагаемых:
на сумму простых слагаемых:  .
. . Подставляем в общую формулу Wa (z):
. Подставляем в общую формулу Wa (z): .
. ,
, . Подставим w = j (T /2)l в выражение Wa (w):
. Подставим w = j (T /2)l в выражение Wa (w): .
. . Поэтому
. Поэтому  .
.

 .
. .
. D (z) = z + kT – 1 = a 0 z + a 1,
D (z) = z + kT – 1 = a 0 z + a 1, где
где  .
.
 .
. .
. - общий коэффициент передачи разомкнутой системы. Тогда
- общий коэффициент передачи разомкнутой системы. Тогда 
 .
. .
. .
.
 ,
,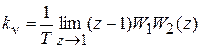 - добротность системы по скорости. Для системы астатической 1-го порядка, передаточная функция которой содержит один полюс z = 1, k n = k / T. Для того чтобы установившееся значение ошибки было равно нулю, необходимо, чтобы C 1 = 0, т. е. k n = ¥. Это возможно, если W 1 W 2(z) имеет два полюса z = 1.
- добротность системы по скорости. Для системы астатической 1-го порядка, передаточная функция которой содержит один полюс z = 1, k n = k / T. Для того чтобы установившееся значение ошибки было равно нулю, необходимо, чтобы C 1 = 0, т. е. k n = ¥. Это возможно, если W 1 W 2(z) имеет два полюса z = 1. .
.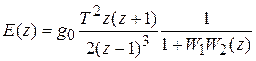 .
.

 - добротность системы по ускорению.
- добротность системы по ускорению. видно, что установившаяся ошибка будет равна нулю, если ka = ¥, т. е. W 1 W 2(z) иметь три полюса z = 1.
видно, что установившаяся ошибка будет равна нулю, если ka = ¥, т. е. W 1 W 2(z) иметь три полюса z = 1.


