Частотные критерии устойчивости

 

Среди частотных критериев устойчивости, используемых в практике анализа устойчивости непрерывных и дискретных систем автоматического управления, наибольшее признание получили критерий годографа характеристического полинома замкнутой системы (известный в отечественной литературе как критерий Михайлова) и критерий Найквиста, обеспечивающий определение устойчивости по виду частотных характеристик разомкнутой системы.

В основу названных выше критериев положено следствие из известного в теории функции комплексной переменной принципа аргумента. Оно устанавливает соответствие между числом корней в левой и правой полуплоскости и суммарным приращением аргумента вектора характеристического полинома замкнутой системы, при изменении частоты в диапазоне 0 £ w £ +¥. Рассмотрим это соответствие.

Характеристическое уравнение замкнутой непрерывной системы

D (s) = a ₀ sⁿ + a ₁ s^{n -1} + ¼ + a_n = 0,

где левая часть уравнения D(s) называется характеристическим полиномом. Его можно представить в соответствии с теоремой Безу следующим образом
D(s) = a₀(s – s₁) (s – s₂) ¼(s – s_i) ¼(s – s_n), где s_i (i =1, 2, ¼, n) – корни характеристического уравнения D(s) = 0; s_i = a_i + jw_i. На комплексной плоскости каждый корень может быть представлен вектором (рис. 4.2). Длина вектора , угол поворота от положительной вещественной полуоси равен аргументу Args_i = arctg(w_i/a_i). Отдельные сомножители D(s) вида (s – s_i) могут быть представлены векторами, проведенными из точек s_i в точки s.

Положим s = j w, тогда вектор (s – s_i) = (j w - s_i) будет скользить своим концом по мнимой оси при изменении частоты +¥ £ w £ ¥.

Приращение аргумента , причем корень s_i, расположенный в левой полуплоскости, обеспечивает приращение аргумента +p (рис. 4.3, а), а корень, находящийся в правой полуплоскости, дает DArg s_i =
= -p (рис. 4.3, б).

Если общее число корней характеристического уравнения n, а в правой полуплоскости находится m корней, то суммарное приращение аргумента D (s)

.

Если изменять частоту только в положительном диапазоне 0 £ w £ ¥, то суммарное приращение аргумента D (s) будет в 2 раза меньше

.

Полученное соотношение положено в основу частотных критериев устойчивости непрерывных систем.

 

Критерий годографа характеристического полинома

 

На основании полученного в предыдущем параграфе соотношения для непрерывных систем и полагая, что в правой полуплоскости нет ни одного корня
(m = 0), находим, что .

Отсюда вытекает следующая формулировка критерия.

Для устойчивости замкнутой непрерывной системы необходимо и достаточно, чтобы при изменении частоты в диапазоне 0 £ w £ ¥ годограф характеристического полинома начинался на положительной вещественной оси и обошел в положительном направлении (против часовой стрелки) последовательно n квадрантов, нигде не обращаясь в нуль и нигде не пересекаясь сам с собой.

Годографы устойчивых систем показаны на рис. 4.4, а, для неустойчивых систем на рис. 4.4, б.

Если систем находится на границе устойчивости, то годограф D (j w) проходит через начало координат.

Положим m = 0 в соотношении, записанном для дискретных систем, получим

,

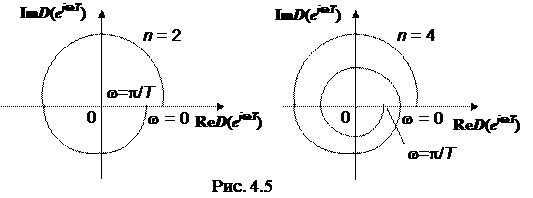
откуда следует следующая формулировка критерия.

Для устойчивости замкнутой дискретной системы необходимо и достаточно, чтобы при изменении частоты в диапазоне 0 £ w £ p/ T годограф характеристического полинома обошел в положительном направлении 2 n квадрантов, нигде не обращаясь в нуль и не пересекаясь сам с собой.

Годографы устойчивых дискретных систем второго и четвертого порядка показаны на рис. 4.5.

Как и отмечалось ранее, крайние точки годографов D (e^{j 0}) и D (e^{j p}) являются вещественными и находятся на вещественной оси.

 

Критерий Найквиста

Критерий Найквиста позволяет оценивать устойчивость замкнутой системы автоматического управления по частотным характеристикам разомкнутой системы. В качестве частотных характеристик используется амплитудно-фазовая (АФХ) характеристика и ЛАФЧХ разомкнутой системы.

Рассмотрим сначала критерий Найквиста на базе АФХ разомкнутой системы.

Пусть передаточная функция разомкнутой системы

.

Передаточная функция замкнутой системы

где A(s) + B(s) = D(s) - характеристический полином замкнутой системы.

Рассмотрим вспомогательную функцию

 

Заметим, что числитель j (s) равен D(s) характеристическому полиному замкнутой системы, а знаменатель A(s) - характеристический полином разомкнутой системы. Заметим также, что степени числителя и знаменателя равны, так как m £ n.

Предположим, что разомкнутая система устойчива, т. е. все корни A (s) = 0 лежат в левой полуплоскости. Для того, чтобы и замкнутая система была устойчивой, необходимо, чтобы все корни D(s) = 0 находились также в левой полуплоскости.

Положим s= j w и будем изменять w от 0 до ¥. Согласно принципа аргумента

.

Это значит, что годограф вспомогательной функции j(j w) при 0 £ w £ ¥ не будет охватывать начало координат (рис. 4.6, а). Заметим, что комплексная передаточная функция разомкнутой системы отличается от j(j w) на единицу

W (j w)=j(j w)-1.

Поэтому вместо j(j w) можно рассматривать W (j w), но в координатах, где мнимая ось перенесена на (-1) (рис. 4.6, б).

Отсюда следует формулировка критерия Найквиста для случая устойчивой разомкнутой системы.

Если разомкнутая система устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы не охватывала критическую точку с координатами (-1, j 0).

На рис. 4.7 показаны различные случаи прохождения АФХ разомкнутой системы относительно критической точки (-1, j 0).

Штриховыми линиями показаны АФХ при уменьшении коэффициента усиления разомкнутых систем:

случай а) – абсолютно устойчивая система;

случай б) – система на границе устойчивости;

случай в) – условно устойчивая система, которая при уменьшении коэффициента усиления может стать неустойчивой;

случай г) – неустойчивая система.

Для астатических систем (n > 0) применение критерия Найквиста имеет свою особенность. Дело в том, что АФХ таких систем в области низких, частот приближаются к одной из осей комплексной плоскости. Поэтому для определения устойчивости по критерию Найквиста необходимо предварительно дополнять АФХ дугами -np/2 окружности бесконечно большого радиуса (рис. 4.8).

Теперь предположим, что разомкнутая система не устойчива, т. е. l корней характеристического уравнения находятся в правой полуплоскости.

Тогда при изменении частоты от 0 до ¥ суммарное приращение аргумента будет

.

Отсюда формулировка критерия Найквиста.

Если разомкнутая система неустойчива, то для того, чтобы была устойчивой замкнутая система, необходимо и достаточно, чтобы АФХ разомкнутой системы охватывала критическую точку в положительном направлении раз, где l – число корней характеристического уравнения разомкнутой системы в правой полуплоскости.

На рис. 4.9 показана АФХ разомкнутой системы, имеющая два корня в правой полуплоскости. Система, имеющая такую АФХ, будет устойчивой в замкнутом состоянии.

При сложной форме АФХ определить число охватов критической точки (-1, j 0) затруднительно. В этом случае удобнее считать число переходов АФХ через отрезок (-¥, -1) отрицательной вещественной оси. Переход сверху вниз считается положительным, снизу вверх – отрицательным. Если АФХ начинается на отрезке (-¥, -1) при w = 0 и заканчивается на нем при w = ¥, то считается, что она совершает ½ перехода.

Формулировка критерия Найквиста по числу переходов будет следующей.

Если разомкнутая система неустойчива, то для того, чтобы разность между числами положительных и отрицательных переходов АФХ разомкнутой системы через отрезок вещественной оси (-¥, -1) была равна , где l – число корней разомкнутой системы в правой полуплоскости.

Так система, АФХ которой показана на
рис. 4.10, будет устойчивой, если число корней в правой полуплоскости l = 2.

Рассмотрим теперь, как будет формироваться критерий Найквиста с использованием логарифмических амплитудно-частотных фазочастотных характеристик. Прежде всего установим, где будет расположена критическая точка с координатами (-1, j 0) в плоскости АФХ разомкнутой системы. Отметим, что критической точке (-1, j 0) соответствует точка, в которой модуль вектора АФХ / W (j w)/ = 1, а угол сдвига j = Arg W (j w) = -180°. В плоскости ЛАФЧХ этой точке соответствует частота, на которой L (w) = 20 lg/ W (j w)/ = 0, т. е. график L (w) пересекает ось частот, и j(w) = -180°, т. е. график j(w) пересекает линию (-180°). Таким образом, если замкнутая система будет находиться на границе устойчивости, то ЛАЧХ и ЛФЧХ разомкнутой системы пересекают линии L (w) = 0 и j(w) = -180° одновременно, на одной и той же частоте (рис. 4.12).

Если же система устойчива в разомкнутом и замкнутом состояниях, то ее АФХ проходит справа от критической точки, т. е. / W (j w)/_{j =-p} < 1.

Отсюда следует первая формулировка критерия Найквиста по ЛАФЧХ разомкнутой системы: если разомкнутая система устойчива, то для устойчивости в замкнутом состоянии необходимо и достаточно, чтобы ЛАЧХ системы пересекала ось частот раньше, чем ЛФЧХ пересечет линию j = -180°.

Иллюстрация взаимного расположения ЛАЧХ и ЛФЧХ разомкнутой системы, устойчивой в замкнутом состоянии, показана на рис. 4.13.

При сложной форме АФХ и ЛАФЧХ может иметь место неоднократное пересечение линии j = -180° характеристикой j(w) на участке частот, где L (w) > 0, т. е. до точки пересечения L (w) оси частот. То же явление может наблюдаться и в плоскости ЛАФЧХ системы, неустойчивой в разомкнутом состоянии. В этом случае проще делать заключение о том, устойчива система или нет в замкнутом состоянии по числу, переходов графика j(w) через линию j = -180° левее точки пересечения графиком L (w) оси частот. Формулировка критерия Найквиста в этом случае следующая: для –устойчивости замкнутой системы необходимо и достаточно, чтобы при положительных значениях ЛАЧХ разность между числом положительных и отрицательных переходов ФЧХ через линию j = -180° равнялась l /2, где l – число корней, расположенных в правой полуплоскости. Положительным считается переход ФЧХ линии j = -180° снизу вверх, отрицательным – сверху вниз. Рис. 4.14 иллюстрирует это положение, сформулированное выше. Характеристика j₁(w) соответствует системе, устойчивой в разомкнутом состоянии и находящейся на границе устойчивости в замкнутом состоянии. Характеристика j₂(w) принадлежит системе устойчивой в разомкнутом и замкнутом состояниях. И, наконец, j₃(w) свидетельствует о неустойчивости в разомкнутом состоянии и устойчивости в замкнутом, если число неустойчивых корней
l = 2.

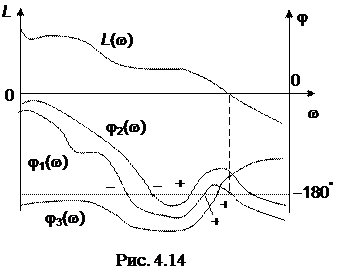Сформулированные выше правила определения (не) устойчивости замкнутой системы по ЛАФЧХ разомкнутой системы полностью применимы и для дискретных систем. Особенностью является лишь то, что ЛФЧХ дискретных систем строятся в функции псевдочастоты l, а в случае формулировки устойчивости для неустойчивой в разомкнутом состоянии дискретной системы l означает число корней, по модулю больше единицы, т. е. находящихся вне круга единичного радиуса.