
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды математических моделей сауСодержание книги
Поиск на нашем сайте
· Математические модели; · Преобразование структурных схем; · Частотные характеристики; · Типовые звенья; · Логарифмическо - частотные характеристики · Математические модели в форме переменных состояния Целью математического описания САУ является составление той или иной математической модели, используемой в дальнейшем для анализа и синтеза САУ. Любая математическая модель является, приближением к действительному состоянию взаимодействия отдельных информационных параметров объекта или всей системы в целом и отражает наиболее существенные взаимосвязи между переменными величинами. Так большинство переменных величин объектов и систем управления подвергается ограничению естественным или искусственным путем. Множество зависимостей между информационными параметрами являются нелинейными и должны быть представлены нелинейными математическими моделями. Однако в рамках настоящего пособия рассматриваются линейные математические модели, так как многие режимы функционирования САУ характеризуются незначительными изменениями переменных величин, в пределах которых зависимости между величинами могут считаться линейными. Системы, работающие в полных диапазонах изменений переменных, а также системы, содержащие элементы с явно выраженными нелинейными характеристиками (например, релейными), являются существенно нелинейными системами и рассматриваются в курсе «Нелинейные системы управления». Различают следующие виды математических моделей САУ: 1) дифференциальные и разностные уравнения систем управления и их элементов; 2) векторно-матричные модели в пространстве состояний; 3) передаточные функции элементов и систем управления; 4) структурные схемы систем управления; 5) направленные графы систем управления; 6) временные характеристики САУ; 7) частотные характеристики САУ. Эти же виды математических моделей в той или иной мере используются и для описания нелинейных САУ. Дифференциально-разностные уравнения САУ Дифференциальные (в частных случаях, алгебраические) уравнения непрерывных систем и разностные уравнения дискретных систем являются основной первичной формой математического описания любой САУ. Они могут использоваться самостоятельно для выполнения задач анализа и синтеза или служить основой для создания других форм математического описания. Дифференциальные и алгебраические уравнения непрерывных САУ составляются на основании изучения и осознания основных физических, химических и информационных процессов, происходящих в объекте управления и системе в целом. Часто для записи уравнений используются уже известные законы, устанавливающие связь между технологическими переменными величинами. Рассмотрим, в качестве примера, составление уравнений для двигателя постоянного тока независимого возбуждения, управляемого изменением напряжения, приложенного к якорю. Модель двигателя (рис.2.1) включает якорную цепь, содержащую сопротивление R я и индуктивность L я якоря с противоэдс якоря E. Питание цепи якоря подается от источника напряжением U. Вал двигателя, вращающийся с угловой скоростью w, соединен с рабочим органом РО, создающим момент сопротивления на валу двигателя.
Уравнение равновесия напряжений электрической цепи якоря двигателя: U - E = i Я R Я + L Я На основании закона электромагнитной индукции противоэдс двигателя: E = C e Ф w, (3.2) где с е – конструктивный коэффициент; Ф – поток возбуждения, принимаемый постоянным; Ф = const. В соответствии с законом Ньютона для вращательного движения уравнение движения вала двигателя: J где J – момент инерции движущихся частей двигателя и рабочего органа, приведенных к валу двигателя; Mg = CМФi Я, (3.4) где CМ – конструктивный коэффициент; Mc - момент сопротивления на валу двигателя. Таким образом, уравнение (3.1 – 3.4) образуют математическую модель двигателя постоянного тока. Два из них (3.1 и 3.3) – дифференциальные уравнения, два другие (3.2 и 3.4) – алгебраические. Все уравнения линейные, так как зависимости E = f (w) и Mg = f (i Я) суть прямые линии (CeФ и CМФ = const), а коэффициенты дифференциальных уравнений (J, R Я, L Я, Me) постоянные. Преобразование Лапласа Несмотря на неограниченные возможности компьютерных технологий по решению систем дифференциальных и разностных уравнений преобразование Лапласа остается по-прежнему широко используемым при решении задач анализа и синтеза САУ. Непрерывным преобразованием Лапласа непрерывной временной функции f (t) называется следующее преобразование
где s = a + j w, a и w - постоянные, j = Приведем в качестве примеров непрерывного преобразования изображения единичной ступенчатой функции f (t) = 1(t).
Основные свойства преобразования Лапласа 1. Свойство линейности. Непрерывное преобразование Лапласа являются линейным, т. е. изображение линейной комбинации функций равно линейной комбинации их изображений. Так если
2. Изображение смещенной функции (теорема сдвига) Сдвигу функции оригинала на t, т. е.
3. Изображение производной (конечной разности) n -порядка Если 4. Изображение интеграла (конечной суммы) функции-оригинала Свойства изменения изображений функции после ее интегрирования или взятия конечной суммы в дискретном варианте является “обратными” по отношению к свойствам дифференцирования или взятия конечных разностей:
Резюмируя свойства 3 и 4 отметим, что s – оператор дифференцирования в непрерывной области; 1/ s – оператор интегрирования в непрерывной области. 5. Свойство изображения свертываемых функций (теорема свертки) Сверткой двух непрерывных называется функция, значения которой вычисляются согласно Формулировка свойства об изображении свертки для непрерывного времени: - изображение свертки равно произведению изображений свертываемых функций. Если
6. Определение начального значения функции оригинала по известному изображению Зная изображение F (s) можно сравнительно просто вычислить начальное и конечное значения функции-оригинала. Начальное значение непрерывной функции
6. Конечное значение функции-оригинала В непрерывном времени
Преобразование дифференциальных и разностных уравнений. Пусть непрерывная система описывается уравнением
где y (t), g (t), f (t) – выходная управляемая величина, управляющее и возмущающее воздействие соответственно; a 0, …, an; b 0, …, bm; c 0, …, ce – постоянные коэффициенты. Предположим, что система работает при нулевых начальных условиях, т. е. при t = 0 имеем
где Y (s), G (s), F (s) – изображения по Лапласу функций y (t), g (t), f (t). Перепишем полученное уравнение в более сжатой форме
Сравнивая полученное уравнение с исходным, приходим к правилу преобразования по Лапласу любого дифференциального уравнения: чтобы получить преобразованное по Лапласу уравнение, необходимо операторы дифференцирования Отметим, что преобразование по Лапласу уравнение является алгебраическим, что в корне облегчает все математические операции при его использовании. Теперь возьмем отношения изображений присутствующих в уравнении величин, принимая одну из них (управление G (s) или возмущение F (s)) равной нулю:
Полученные отношения представляют собой передаточные функции системы по управляющему и возмущающему воздействиям:
Передаточной функцией системы (элемента системы) называется отношение изображений по Лапласу выходной и входной величин при нулевых начальных условиях. Понятие передаточной функции является одним из фундаментальных в теории автоматического управления и широко используется на различных стадиях анализа и синтеза систем управления.
Структурные схемы САУ Структурной схемой САУ называется графическая форма представления математической модели системы в виде соединения отдельных звеньев, каждое из которых задано каким-либо математическим оператором преобразования входного сигнала в выходной. Операторы преобразования могут быть заданы символами преобразования во временной области или в области изображений (передаточные функции) или с помощью статических и динамических характеристик. Звенья представляются на структурных схемах с помощью прямоугольников. Соединение их осуществляется стрелками, указывающими направления передачи сигналов управления. Прохождение сигналов управления против направления, указанного стрелками, невозможно. Различные варианты представления звеньев структурной схемы показаны на рис. 3.2.
Отметим, что звенья, выполняющие математические операции «умножение» и «деление», изображаются также прямоугольниками. Звенья же, выполняющие алгебраические операции «сложение» и «вычитание», изображаются кружками с подходящими и отходящими стрелками. Причем, отсутствие у подходящих стрелок каких-либо математических знаков означает суммирование сигналов. Присутствие знаков у стрелки означает, что этот сигнал вычитается из сигнала, соответствующего другой стрелке. Кроме общих структурных схем широко используются детализированные структурные схемы, состоящие только из безинерционных масштабных звеньев и идеальных интегрирующих звеньев с полностью вскрытыми связями между ними. Детализированная структурная схема (ДСС) составляется из исходной общей схемы путем преобразования звеньев с так называемыми «сложными» передаточными функциями. «Детализация» звена со «сложной» передаточной функцией осуществляется в следующей последовательности: 1) записывается операторное уравнение звена по исходной передаточной функции. W (s)=
1) Уравнение разрешается относительно старшей производной выходной величины x 2:
2) Обе части уравнения делятся на коэффициент при x 2 в левой части с целью получить выражение для x 2
Пользуясь указанной последовательностью удается легко построить ДСС для звеньев с передаточными функциями невысокого порядка (n Приведем несколько примеров. Пример1: Построить ДСС звена с передаточной функцией W (s)=
Пример 2: Передаточная функция исходного звена
 T 2 sx 2 + x 2 = T 1 sx 1 + x 1; T 2 sx 2 = T 1 sx 1 + x 1 - x 2; T 2 sx 2 + x 2 = T 1 sx 1 + x 1; T 2 sx 2 = T 1 sx 1 + x 1 - x 2; x 2 =  x 1 + x 1 +  (x 1 - x 2); (x 1 - x 2);
 x 1 + x 1 +  (x 1 - x 2). (x 1 - x 2).
Пример 3: Составить ДСС стандартного звена 2-го порядка с передаточной функцией W (s)=
В случае исходной передаточной функции с n > 2 целесообразно пользоваться процедурой, называемой непосредственной декомпозицией. Суть ее заключается в том, что вводится фиктивная переменная x (s) и на нее умножается числитель и знаменатель передаточной функции:
Приравнивание числителя и знаменателя дает x 2(s)= x 1(s)=
Последнее выражение используется для определения x (s) путем записи его относительно старшей производной с последующим делением на коэффициент при старшей производной:  = =  x (s) = x (s) = =  . После определения x (s) строится схема вычисления x 2(s) согласно первого выражения (3.5.). Общая схема построения ДСС «сложного» звена представлена на рис. 3.3. . После определения x (s) строится схема вычисления x 2(s) согласно первого выражения (3.5.). Общая схема построения ДСС «сложного» звена представлена на рис. 3.3.
В заключении отметим, что ДСС непрерывных систем нашли широкое применение для составления уравнений состояния, а также для составления и расчета параметров модели при аналоговом моделировании. Пусть передаточная функция дискретного фильтра (регулятора) задана в виде: W (z)=
Cтруктурная схема программирования, реализующая полученные разностные уравнения, представлена на рис. 3.4. В схеме элементы задержки на один такт квантования обозначены как «Зад». Порядки числителя и знаменателя передаточной функции приняты равными m = k.
3.3. Преобразование структурных схем
Преобразование структурных схем линейных непрерывных систем управления базируется на выполнении двух важнейших принципов линейных преобразований: 1) аддитивности или суперпозиции (наложения) и 2) коммутативности (перестановки местами). Преобразование структурных схем формулируется в виде правил преобразований, поэтому далее будем рассмотрено совокупность таких правил.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 2174; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.011 с.) |

 Изучаемые вопросы:
Изучаемые вопросы:
 (3.1)
(3.1) = Mg - Mc, (3.3)
= Mg - Mc, (3.3) ,
,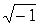 . Преобразуемая функция f (t) часто называется оригиналом, а F (s) – изображением функции f (t). К функции f (t) предъявляется требование, чтобы она была однозначной и удовлетворяла условию f (t) = = 0 при t < 0.
. Преобразуемая функция f (t) часто называется оригиналом, а F (s) – изображением функции f (t). К функции f (t) предъявляется требование, чтобы она была однозначной и удовлетворяла условию f (t) = = 0 при t < 0. .
. , то
, то .
. соответствует умножение непрерывного изображения на
соответствует умножение непрерывного изображения на  :
: .
. , то
, то 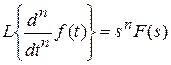 , при f (0) = 0 и всех
, при f (0) = 0 и всех  ,
, 
 для непрерывного времени.
для непрерывного времени. и
и  , то
, то .
. .
. .
.
 ,
,

 . Подвергнем заданное дифференциальное уравнение преобразованию Лапласа, используя свойства линейности и изображения производной,
. Подвергнем заданное дифференциальное уравнение преобразованию Лапласа, используя свойства линейности и изображения производной,

 заменить комплексными операторами s = a + j w, а все временные функции заменить их изображением.
заменить комплексными операторами s = a + j w, а все временные функции заменить их изображением. .
. .
.
 =
=  =
=  , m
, m  n.
n. =
=  ;
; ;
;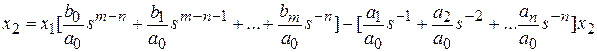 .
. .
.

 x 1 -
x 1 -  x 2 =
x 2 =  x 1 -
x 1 - 
 .
.
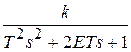 ; T 2 s 2 x 2 + 2e Tsx 2 + x 2 = kx 1;
; T 2 s 2 x 2 + 2e Tsx 2 + x 2 = kx 1;  (kx 1 - 2e Tsx 2 - x 2)
(kx 1 - 2e Tsx 2 - x 2)
 .
. x (s), (3.5)
x (s), (3.5) x (s) (3.6)
x (s) (3.6)
 , где m и k – целые числа, чаще всего m = k; Коэффициенты bm и ak не равны нулю.
, где m и k – целые числа, чаще всего m = k; Коэффициенты bm и ak не равны нулю.



