
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическое представление дискретных функций
В рассматриваемых системах непрерывная часть имеет значительный вес в сравнении с дискретной и, кроме того, импульсные элементы преобразуют непрерывные сигналы в последовательность импульсов определенной формы. Появляется необходимость учитывать реальную форму импульсов и отразить зависимость того или иного параметра импульсов от мгновенных значений непрерывного сигнала. Использование аппарата решетчатых функций для таких систем оказалось недостаточным. Решетчатая функция дискретного аргумента не может быть непосредственно подвергнута преобразованию Лапласа. Значит, отсутствует возможность составить математические модели, например, в форме передаточных функций или частотных характеристик, широко используемых для моделирования непрерывных частей таких систем. Возникшее противоречие было преодолено за счет применения аппарата d-функций. Для того, чтобы описать дискретные сигналы с помощью d-функций было предложено заменять реальные импульсные элементы (РИЭ) комбинациями из идеальных импульсных элементов (ИИЭ) и формирующих элементов (ФЭ) как показано на рис. 5.3. Идеальным импульсным элементом называется абстрактный математический элемент, который под воздействием непрерывного сигнала на его входе генерирует мгновенные типа d-функций импульсы, следующие с интервалом, равным периоду дискретности РИЭ, и по площади равные значения непрерывного сигнала в моменты квантования. Последовательность d-функций на выходе ИИЭ
Формирующим называется элемент, который под воздействием мгновенных модулированных по площади импульсов формирует на выходе импульсы, соответствующие выходному сигналу РИЭ. Для описания ФЭ привлекается понятие импульсной переходной характеристики. Действительно, каждый импульс на выходе ФЭ есть реакция на входной мгновенный импульс типа d-функции, т. е. его импульсная переходная характеристика w (t). Подвергнув w (t) преобразованию Лапласа, получают передаточную функцию формирующего элемента
Так, например, для импульса прямоугольной формы, единичной амплитуды и длительностью t = g T
Передаточная функция ФЭ При g = 1 получаем передаточную функцию
Подобным образом получены передаточные функции часто встречающихся на практике импульсных элементов. Составив математическое описание формирующего элемента, его объединяют с непрерывной частью системы, благодаря чему получается приведенная непрерывная часть (ПНЧ) – рис. 5.5.
Преимуществом такого представления участка дискретно-непрерывной системы является то, что выходной сигнал ИИЭ Uf *(t) может быть преобразован по Лапласу, тогда как для сигнала f *(t) на выходе РИЭ преобразование Лапласа недопустимо. К функции дискретного аргумента f (nT) или f [(n + s) T ] непрерывное преобразование Лапласа не может быть применено, так как функции f (nT) и f [(n + s) T ] не являются однозначными. Для того, чтобы выполнить преобразование Лапласа над функцией дискретного аргумента, последняя должна быть представлена как бесконечная сумма модулированных по площади d-функций
Преобразование Лапласа выполненное над суммой модулированных d-функций, называется дискретным преобразованием Лапласа
так как
Для символического обозначения дискретного преобразования Лапласа используется символ
Для записи преобразования над смещенной дискретной функцией
Результатом дискретного преобразования функции f (t) является функция трансцендентная, использование которой в преобразованиях затруднительно. Поэтому для описания дискретных систем получило распространение так называемое Z -преобразование, получающееся из дискретного преобразования Лапласа путем формальной замены
Таким образом,
Приведем в качестве примеров непрерывного – и Z -преобразований изображения единичной ступенчатой функции f (t) = 1(t).
5.3. Z-преобразования
1. Свойство линейности. Оба преобразования: непрерывное Лапласа и Z -преобразование, - являются линейными, т. е. изображение линейной комбинации функций равно линейной комбинации их изображений.
Так если
· Изображение смещенной функции (теорема сдвига) Сдвигу функции оригинала на t, т. е.
Если сдвиг t = mT (T - интервал дискретности), то Z – или Z s - изображения функции f (t) умножаются на Z-m
Частотные случаи последнего свойства: 1) m = +1; Т. е. Z -1 – оператор запаздывания на один период дискретности; 2) m = -1; Z – оператор опережения на один период дискретности. · Изображение производной (конечной разности) n -порядка Если Аналогично для Z -преобразования (приводим формулировку свойства для s = 0) взятию разности k -го порядка дискретной функции f (nT) соответствует умножение ее изображения на 2. Изображение интеграла (конечной суммы) функции-оригинала Свойства изменения изображений функции после ее интегрирования или взятия конечной суммы в дискретном варианте является “обратными” по отношению к свойствам дифференцирования или взятия конечных разностей:
Резюмируя свойства 3 и 4 отметим, что s – оператор дифференцирования в непрерывной области; 1/ s – оператор интегрирования в непрерывной области; · Свойство изображения свертываемых функций (теорема свертки) Сверткой двух непрерывных или дискретных функций называется функция, значения которой вычисляются согласно Формулировка свойства об изображении свертки одинакова для непрерывного и дискретного времени: - изображение свертки равно произведению изображений свертываемых функций. Если
Если
3. Определение начального значения функции оригинала по известному изображению Зная изображение (F (s) в непрерывном случае и F (z) или F (z,s) в дискретном случае) можно сравнительно просто вычислить начальное и конечное значения функции-оригинала. Начальное значение непрерывной функции
Начальное значение дискретной функции
4. Конечное значение функции-оригинала В непрерывном времени В дискретном времени
Рассмотрим еще несколько свойств, полезных для выполнения несложных преобразований. 5. Свойство изображения функции, умноженной на Для дискретного времени это свойство записывается следующим образом: Если В частном случае s = 0 имеем
Записанное свойство позволяет без труда найти изображение экспоненциальной функции
Для непрерывного времени в рамках этого свойства определяется изображение
6. Свойство изображения функции, умноженной на tm ( m – целое число) Это свойство имеет особое значение для дискретных систем, так как для непрерывных систем составлены подробнейшие таблицы соответствий функций и их изображений [6]. Для дискретных систем свойство формулируется отдельно для случаев s = 0 и s ¹ 0. Для s = 0 имеем
Словами: умножению функции-оригинала tm соответствует, с точностью до множителя, взятие m -производной в области изображений.
Пример.
Для s ¹ 0 выражение изображения находится более сложно:
Здесь
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 369; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.74.227 (0.023 с.) |
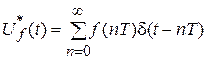
 .
. .
. .
. так называемого экстраполятора нулевого порядка. В технике такая передаточная функция соответствует преобразователю “код – напряжение”.
так называемого экстраполятора нулевого порядка. В технике такая передаточная функция соответствует преобразователю “код – напряжение”.
 .
.

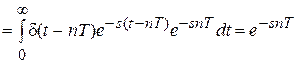
 .
. .
. .
. называется Z - преобразованием функции f (t). Если в рассмотрение вводится местный локальный сдвиг s, то вводится понятие модифицированного Z -преобразования.
называется Z - преобразованием функции f (t). Если в рассмотрение вводится местный локальный сдвиг s, то вводится понятие модифицированного Z -преобразования.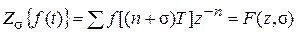 .
. .
. (сумма бесконечной геометрической прогрессии
(сумма бесконечной геометрической прогрессии  , где a = 1, q = z -1).
, где a = 1, q = z -1). , то
, то .
. соответствует умножение непрерывного изображения на
соответствует умножение непрерывного изображения на  :
: .
. .
. .
. ;
; , то
, то 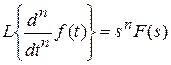 , при f (0) = 0 и всех
, при f (0) = 0 и всех  ,
,  :
:  , где
, где  .
.

 - оператор суммирования в дискретном времени;
- оператор суммирования в дискретном времени;  - оператор взятия конечной разности 1-го порядка.
- оператор взятия конечной разности 1-го порядка. для непрерывного времени и
для непрерывного времени и 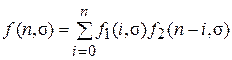 для дискретного времени.
для дискретного времени. и
и  , то
, то .
. и
и  , то
, то .
. .
. .
. .
. и при s ¹ 0
и при s ¹ 0 .
.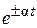
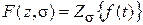 , то
, то 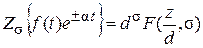 , где d =
, где d =  .
. , где d =
, где d = 

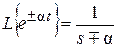 .
. .
.
 .
. .
.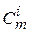 - число сочетаний из m элементов по i.
- число сочетаний из m элементов по i.


