
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь спектров непрерывного и дискретного сигналовСодержание книги
Поиск на нашем сайте
Для выяснения соотношения между Z -преобразованием и непрерывным преобразованием Лапласа, а также соотношения частотных свойств дискретного и непрерывного сигналов рассмотрим связь спектров этих сигналов. Спектр непрерывного сигнала x (t) определяется его преобразованием Фурье Чтобы найти выражение спектра дискретного сигнала, его надо предварительно представить в непрерывной форме с помощью d-функций
где U *(t) – последовательность d-функций, следующая с периодом T. Как периодическую функцию U *(t) можно разложить в ряд Фурье
где
следовательно все коэффициенты ряда Фурье равны независимо от значения k. Для всей суммы d-функций
Подставляя U *(t) в выражение сигнала, получим
В таком виде сигнал x *(t) может быть подвергнут преобразованию Фурье:
где Общий вывод: спектр дискретного сигнала представляет бесконечную сумму (рис. 5.6) смещенных спектров непрерывного сигнала.
Это значит, что при определенной частоте квантования частотные характеристики дискретных систем будут представлять сумму смещенных частотных характеристик соответствующих непрерывных систем. Это также означает, что если максимальная частота спектра непрерывного сигнала (wм) или, максимальная частота пропускания непрерывной части системы (wп) меньше половины частоты квантования w0, то наложение отдельных составляющих спектра не будет, и характеристики дискретной системы в существенном диапазоне частот будут совпадать с характеристиками непрерывной системы. И так для системы необходимо Для неискаженной передачи непрерывного сигнала его дискретными значениями необходимо, чтобы максимальная частота спектра непрерывного сигнала Последнее условие является стержнем знаменитой импульсной теоремы Котельникова-Шеннона, согласно которой частота квантования w0 =2p/ T должна быть по крайней мере в 2 раза больше максимальной частоты спектра непрерывного сигнала, передаваемого его дискретными значениями.
5.3.2. Связь между непрерывным преобразованием Лапласа
Из выражений непрерывных преобразований Лапласа и Фурье, приводимых ранее, следует, что
Символически эту связь записывают следующим образом:
что символически означает Записанные выражения связи F (z), F (z, s), F (s) имеют главным образом, теоретическое значение и не используются для практического определения F (z) и F (z, s) по F (s). Существует два способа практического перехода от F (s) к F (z) и F (z, s). 1 способ. Предварительно определяется временная функция, соответствующая исходному изображению Чтобы облегчить переход в дискретную область, можно предварительно разложить F (s) на сумму простых слагаемых. Пример. Пусть Разложение на простые слагаемые дает
Из таблиц соответствия имеем:
2 способ. Осуществляется непосредственный переход от F (s) к F (z), используя таблицу соответствия изображений [6]. Если в таблице нет изображения, соответствующего заданному F (s), выполняют разложение F (s)на сумму более простых выражений. Пример. Пусть
Частный случай, важный в практике записи Z -изображений по заданному F (s). Если Пример. Пусть
Окончательно
5.3.3. Обратное преобразование Лапласа
Обратным преобразованием Лапласа
Обратным Z -преобразованием Отметим ограничения, которые следует иметь в виду, выполняя обратное преобразование Лапласа или обратное Z -преобразование. 1. Не каждая функция F (s) имеет обратное преобразование. Существование обратного преобразования определяется необходимыми и достаточными условиями, накладываемыми на F (s). 2. Прямое преобразование Лапласа 3. Обратное Z – или Z s - преобразование, если оно существует, позволяет определить лишь последовательность отдельных значений непрерывной функции-оригинала, существующих в моменты времени t = nT или Существует два общих практических способа определения обратных преобразований как для непрерывных, так и для дискретных систем. 1. Использование таблиц обратных преобразований Лапласа и обратных Z –преобразований, например в [6]. Если исходного F (s) и F (z) изображения нет в таблице следует использовать разложение его на сумму или произведение изображений, имеющихся в таблице. 2. Использование формулы обращения. Для непрерывного изображения
Значение контурного интеграла определяется в открытом интервале, где f (t) ограничена и имеет конечное число точек экстремума и разрыва. Решение часто удается получить при помощи теоремы о вычетах:
где z 1, z 2, …, zn особые точки Вычисление интеграла обращения как суммы вычетов широко используется в различных программных продуктах, используемых при компьютерном моделировании систем автоматического управления. Для дискретного изображения формула обращения имеет вид
Контур интегрирования R должен охватывать начало координат плоскости Z и все особые точки подынтегральной функции. Как и в непрерывном случае, круговой интеграл обычно рассчитывается как сумма вычетов подынтегральной функции в особых точках:
N – число вычетов; N = q + 1 для n = q для n > 0, где q – число особых точек функции F (z,s). Вычеты вычисляются следующим образом: - для простого полюса
- для кратного полюса кратности m
Кроме двух общих методов, в случае обратного Z –преобразования используется также разложение F (z,s) в ряд по возрастающим степеням z -1 в соответствии с основной формулой Z –преобразования
Когда F (z,s) представлено рациональной дробью разложение по степеням z -1 может быть выполнено простым делением числителя на знаменатель. Пример. Пусть
Получаем f (n) = 1 0.2 0.04 0.008. При более сложных выражениях F (z) и F (z,s) лучше использовать вычисление по рекуррентной формуле:
Здесь b 0, …, bk, …, bp – коэффициенты числителя F (z,s) a 0, …, ai, …, aq – коэффициенты знаменателя F (z,s). При q = p формулы значительно упрощаются
Аналогично преобразованию дифференциального уравнения непрерывной системы осуществляется Z -преобразование разностного уравнения дискретной системы. Пусть дискретная система описывается уравнением
Подвергнем это разностное уравнение Z -преобразованию, принимая начальные условия нулевыми:
Записывая полученное уравнение в сжатой форме, получим
Беря отношения Z -изображений, получим передаточные функции дискретной системы по управляющему и возмущающему воздействиям:
Для дискретно-непрерывной системы определение дискретной передаточной функции выполняется на основе перехода от непрерывной передаточной функции приведенной непрерывной части к ее дискретному эквиваленту в Z -области. Покажем этот переход на примере разомкнутой дискретно-непрерывной системы с одним импульсным элементом на ее входе (рис. 5.7). На схеме
Если вместо непрерывного сигнала y (t)отмечать лишь его дискретные значения y (nT) или y [(n + s) T ], то получим решетчатую функцию y (n) или y (n, s):
Подвергнем эту решетчатую функцию модифицированному Z -преобразованию
С учетом теоремы свертки имеем
Таким образом
Здесь
Структурные схемы
В структурных схемах дискретных систем импульсные (дискретные) элементы изображаются ключами (рис. 5.8.). Иногда ключ снабжается замыкающей стрелкой и большой буквой T, которая означает, что элемент осуществляет квантования с периодом T.
Идеальный импульсный элемент изображается прямоугольником с символом Формирующий элемент изображается как обычное непрерывное звено прямоугольником с записью его передаточной функции (рис. 5.9, б).
Кроме общих структурных схем широко используются детализированные структурные схемы, состоящие только из безинерционных масштабных звеньев и идеальных интегрирующих звеньев с полностью вскрытыми связями между ними.
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1122; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.103.14 (0.007 с.) |

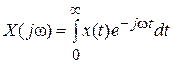 , где w = 2p f – круговая частота сигнала, -¥ £ w £ ¥.
, где w = 2p f – круговая частота сигнала, -¥ £ w £ ¥. ,
, ,
, - круговая частота квантования, Uk – коэффициент ряда Фурье:
- круговая частота квантования, Uk – коэффициент ряда Фурье: ;
;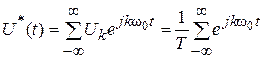 .
. .
.
 - смещенный на k w0 спектр непрерывного сигнала.
- смещенный на k w0 спектр непрерывного сигнала.
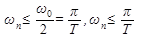 .
. .
.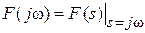 и
и  . Используем эти соотношения для преобразований дискретных сигналов и получим
. Используем эти соотношения для преобразований дискретных сигналов и получим 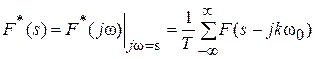 . Если ввести замену
. Если ввести замену 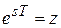 , получим связь непрерывного преобразования Лапласа и Z -преобразования
, получим связь непрерывного преобразования Лапласа и Z -преобразования .
. при s = 0 и
при s = 0 и  ,
, .
. .
. .
.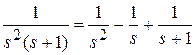 .
. . Таким образом
. Таким образом  . Подвергая f (t) Z -преобразованию, получим:
. Подвергая f (t) Z -преобразованию, получим: .
. . Представим заданное F (s) суммой слагаемых
. Представим заданное F (s) суммой слагаемых  , где
, где  . Определим модифицированное Z -преобразование
. Определим модифицированное Z -преобразование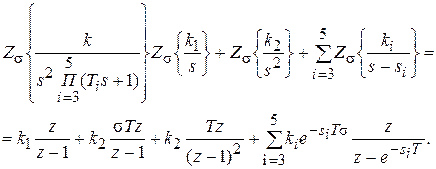
 , то
, то  .
. .
. .
. .
. .
. называется определение временной функции f (t), для которой прямое преобразование Лапласа
называется определение временной функции f (t), для которой прямое преобразование Лапласа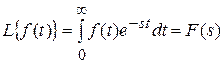 .
.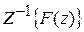 или
или  называется определение дискретной функции времени f (nT) (f [(n + s) T ]), для которой
называется определение дискретной функции времени f (nT) (f [(n + s) T ]), для которой  или
или 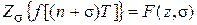 .
. единственно для каждой f (t), имеющей такое преобразование. Обратное утверждение, в общем случае, несправедливо. Различные разрывные функции могут иметь одинаковое преобразование Лапласа. Например, единичная ступенчатая функция f (t) = = 0 для t < 0 и f (t) = 1 для t > 0 имеет преобразование Лапласа 1/ s независимо от значения, принимаемого при t = 0.
единственно для каждой f (t), имеющей такое преобразование. Обратное утверждение, в общем случае, несправедливо. Различные разрывные функции могут иметь одинаковое преобразование Лапласа. Например, единичная ступенчатая функция f (t) = = 0 для t < 0 и f (t) = 1 для t > 0 имеет преобразование Лапласа 1/ s независимо от значения, принимаемого при t = 0. .
. ,
,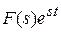 .
. .
. .
.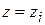
 ;
;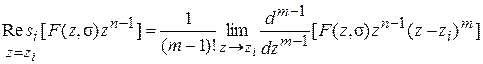 .
. .
. .
.
 .
.



 .
.
 .
. Так как входной сигнал приведенной непрерывной части представляет собой сумму модулированных по площади входным сигналом g (t) d-функций, выходной сигнал y (t) будет представлять сумму реакции ПНЧ на d-функции; т. е. сумму функций веса ПНЧ
Так как входной сигнал приведенной непрерывной части представляет собой сумму модулированных по площади входным сигналом g (t) d-функций, выходной сигнал y (t) будет представлять сумму реакции ПНЧ на d-функции; т. е. сумму функций веса ПНЧ
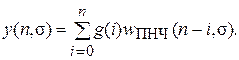
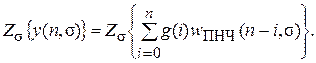

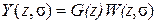 .
. - дискретная передаточная функция разомкнутой дискретно-непрерывной системы. С одной стороны, она связывает Z -изображения дискретных сигналов, с другой стороны, она определяется как Z -форма передаточной функции приведенной непрерывной части.
- дискретная передаточная функция разомкнутой дискретно-непрерывной системы. С одной стороны, она связывает Z -изображения дискретных сигналов, с другой стороны, она определяется как Z -форма передаточной функции приведенной непрерывной части. T T
T T
 - функции внутри (рис. 5.9, а).
- функции внутри (рис. 5.9, а). x (t) u*x(t) u*x(t) x*(t)
x (t) u*x(t) u*x(t) x*(t)


