
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод гармонической линеаризацииСодержание книги
Поиск на нашем сайте
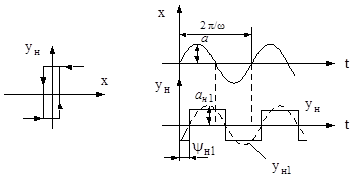
Идея метода гармонической линеаризации принадлежит Н.М. Крылову и Н.Н. Боголюбову и базируется на замене нелинейного элемента системы линейным звеном, параметры которого определяются при гармоническом входном воздействии из условия равенства амплитуд первых гармоник на выходе нелинейного элемента и эквивалентного ему линейного звена. Данный метод может быть использован в том случае, когда линейная часть системы является низкочастотным фильтром, т.е. отфильтровывает все возникающие на выходе нелинейного элемента гармонические составляющие, кроме первой гармоники. Коэффициенты гармонической линеаризации и эквивалентные комплексные коэффициенты передачи нелинейных элементов. В нелинейной системе (рис. 6.1) параметры линейной части и нелинейного элемента выбирают таким образом, чтобы существовали симметричные периодические колебания с частотой w. В основе метода гармонической линеаризации нелинейностей (рис. 6.10), описываемых уравнением yн = F(x), (6.17) лежит предположение, что на вход нелинейного элемента подается гармоническое воздействие с частотой w и амплитудой a, т.е.
x = a sin y, где y = wt, (6.18)
а из всего спектра выходного сигнала выделяется только первая гармоника yн1 = a н1 sin(y + yн1), (6.19)
где a н1 - амплитуда а yн1 - фазовый сдвиг; при этом высшие гармоники отбрасываются и устанавливается связь между первой гармоникой выходного сигнала и входным гармоническим воздействием нелинейного элемента.
Рис. 6.8 В случае нечувствительности нелинейной системы к высшим гармоникам нелинейный элемент может быть в первом приближении заменен некоторым элементом с эквивалентным коэффициентом передачи, который определяет первую гармонику периодических колебаний на выходе в зависимости от частоты и амплитуды синусоидальных колебаний на входе. Для нелинейных элементов с характеристикой (6.17) в результате разложения периодической функции F(x) в ряд Фурье при синусоидальных колебаниях на входе (6.18) получим выражение для первой гармоники сигнала на выходе yн1 = b1F siny + a1F cosy, (6.20) где b1F, a1F - коэффициенты разложения в ряд Фурье, определяющие амплитуды соответственно синфазной и квадратурной составляющих первой гармоники, которые определяются по формулам:
Так как px = a w cos y, где p = d/dt,
то связь между первой гармоникой периодических колебаний на выходе нелинейного элемента и синусоидальными колебаниями на его входе можно записать в виде yн1 = [q + где q = b1F/ a, q¢ = a1F/ a. Последнее уравнение называется уравнением гармонической линеаризации, а коэффициенты q и q¢ - коэффициентами гармонической линеаризации. Таким образом, нелинейный элемент при воздействии гармонического сигнала с точностью до высших гармоник описывается уравнением (6.21), которое является линейным. Это уравнение нелинейного элемента отличается от уравнения линейного звена тем, что его коэффициенты q и q¢ изменяются при изменении амплитуды a и частоты w колебаний на входе. Именно в этом заключается принципиальное отличие гармонической линеаризации от обычной, коэффициенты которой не зависят от входного сигнала, а определяются только видом характеристики нелинейного элемента. Для различных видов нелинейных характеристик коэффициенты гармонической линеаризации сведены в таблицу. В общем случае коэффициенты гармонической линеаризации q(a, w) и q¢(a, w) зависят от амплитуды a и частоты w колебаний на входе нелинейного элемента. Однако, для статических нелинейностей эти коэффициенты q(a) и q¢(a) являются функцией только амплитуды a входного гармонического сигнала, а для статических однозначных нелинейностей коэффициент q¢(a) = 0. Подвергнув уравнение (6.21) преобразованию по Лапласу при нулевых начальных условиях с последующей заменой оператора s на jw (s = jw), получим эквивалентный комплексный коэффициент передачи нелинейного элемента
WЭ(jw, a) = q + jq¢ = AЭ(w, a) e jyэ(w, a), (6.22)
где модуль и аргумент эквивалентного комплексного коэффициента передачи связаны с коэффициентами гармонической линеаризации выражениями AЭ(w, a) = mod WЭ(jw, a) = yЭ(w, a) = arg WЭ(jw, A) = arctg[q¢(a, w)/q(a, w)]. Эквивалентный комплексный коэффициент передачи нелинейного элемента позволяет определить амплитуду и фазовый сдвиг первой гармоники (6.19) на выходе нелинейного элемента при гармоническом воздействии (6.18) на его входе, т.е. a н1 = a ´AЭ(w, a); yн1 = yЭ(w, a).
Исследование симметричных периодических режимов в нелинейных системах. При исследовании нелинейных систем на основе метода гармонической линеаризации в первую очередь решают вопрос о существовании и устойчивости периодических режимов. Если периодический режим устойчив, то в системе существуют автоколебания с частотой w0 и амплитудой a 0.
Рассмотрим нелинейную систему (рис. 6.5), включающую в себя линейную часть с передаточной функцией
и нелинейный элемент с эквивалентным комплексным коэффициентом передачи WЭ(jw, a) = q(w, a) + jq¢(w, a) = AЭ(w, a) e jyэ(w, a). (6.24)
Принимая во внимание выражение (6.21), можно записать уравнение нелинейной системы {A(p) + B(p)´[q(w, a) + Если в замкнутой нелинейной системе возникают автоколебания x = a 0 sin w0t с постоянной амплитудой и частотой, то коэффициенты гармонической линеаризации оказываются постоянными, а вся система стационарной. Для оценки возможности возникновения автоколебаний в нелинейной системе методом гармонической линеаризации необходимо найти условия границы устойчивости, как это делалась при анализе устойчивости линейных систем. Периодическое решение существует, если при a = a 0 и w = w0 характеристическое уравнение гармонически линеаризованной системы A(p) + B(p)´[q(w, a) + имеет пару мнимых корней li = jw0 и li+1 = -jw0. Устойчивость решения необходимо оценить дополнительно. В зависимости от методов решения характеристического уравнения различают методы исследования нелинейных систем. Аналитический метод. Для оценки возможности возникновения в нелинейной системе автоколебаний в гармонически линеаризованный характеристический полином системы вместо p подставляют jw D(jw, a) = A(jw) + B(jw)´[q(w, a) + jq¢(w, a)]. (6.27) В результате получают уравнение D(jw, a) = 0, коэффициенты которого зависят от амплитуды и частоты предполагаемого автоколебательного режима. Выделив вещественную и мнимую части
Re D(jw, a) = X(w, a); Im D(jw, a) = Y(w, a), получим уравнение X(w, a) + jY(w, a) = 0. (6.28)
Если при действительных значениях a 0 и w0 выражение (6.28) удовлетворяется, то в системе возможен автоколебательный режим, параметры которого рассчитываются по следующей системе уравнений:
Из выражений (6.29) можно найти зависимость амплитуды и частоты автоколебаний от параметров системы, например, от коэффициента передачи k линейной части системы. Для этого необходимо в уравнениях (6.29) коэффициент передачи k считать переменной величиной, т.е. эти уравнения записать в виде:
По графикам a 0 = f(k), w0 = f(k) можно выбрать коэффициент передачи k, при котором амплитуда и частота возможных автоколебаний имеет допустимые значения или вообще отсутствует. Частотный метод. В соответствии с критерием устойчивости Найквиста незатухающие колебания в линейной системе возникают в том случае, когда амплитудно-фазовая характеристика разомкнутой системы проходит через точку с координатами [-1, j0]. Данное условие является также условием существования автоколебаний в гармонически линеаризованный нелинейной системе, т.е.
Wн(jw, a) = -1. (6.31)
Так как линейная и нелинейная части системы соединены последовательно, то частотная характеристика разомкнутой нелинейной системы имеет вид Wн(jw, a) = Wлч(jw)´WЭ(jw, a). (6.32)
Тогда в случае статической характеристики нелинейного элемента условие (6.31) принимает вид Wлч(jw) = - Решение уравнения (6.33) относительно частоты и амплитуды автоколебаний можно получить графически как точку пересечения годографа частотной характеристики линейной части системы Wлч(jw) и годографа обратной характеристики нелинейной части
Рис. 6.9
Для устойчивости автоколебательного режима с частотой w0 и амплитудой a 0 требуется, чтобы точка на годографе нелинейной части - На рис. 6.9 дан пример расположения годографов для случая, когда в нелинейной системе существуют устойчивые автоколебания, так как a 3 < a 0 < a 4 . Исследование по логарифмическим частотным характеристикам. При исследовании нелинейных систем по логарифмическим частотным характеристикам условие (6.31) переписывают отдельно для модуля и аргумента эквивалентного комплексного коэффициента передачи разомкнутой нелинейной системы mod Wлч(jw)Wэ(jw, a) = 1; arg Wлч(jw)Wэ(jw, a) = - (2k+1)p, при k=0, 1, 2,... с последующим переходом к логарифмическим амплитудной и фазовой характеристикам
Lлч(w) + Lэ(w, a) = 0; (6.34) yлч(w) + yэ(w, a) = - (2k+1)p, при k=0, 1, 2,... (6.35)
Условия (6.34) и (6.35) позволяют определить амплитуду a 0 и частоту w0 периодического решения уравнения (6.25) по логарифмическим характеристикам линейной части системы Lлч(w), yлч(w) и нелинейного элемента Lэ(w, a), yэ(w, a). Автоколебания с частотой w0 и амплитудой a 0 будут существовать в нелинейной системе, если периодическое решение уравнения (6.25) устойчиво. Приближенный метод исследования устойчивости периодического решения заключается в том, что исследуется поведение системы при частоте w = w0 и значениях амплитуды a = a 0 + D a и a = a 0 - D a, где D a > 0 - малое приращение амплитуды. При исследовании устойчивости периодического решения при a 0 + D a и a 0 - D a по логарифмическим характеристикам пользуются критерием устойчивости Найквиста. В нелинейных системах с однозначными статическими характеристиками нелинейного элемента коэффициент гармонической линеаризации q¢(a) равен нулю, а следовательно, равен нулю и фазовый сдвиг yэ(a), вносимый элементом. В этом случае периодическое решение уравнения системы [A(p) + B(p)´q(a)]x = 0 (6.36) существует, если выполняются условия:
Lлч(w) = - Lэ(a); (6.37) yлч(w) = - (2k+1)p, при k=0, 1, 2,... (6.38)
Уравнение (6.38) позволяет определить частоту w = w0 периодического решения, а уравнение (6.37) - его амплитуду a = a 0.
При сравнительно простой линейной части решения этих уравнений могут быть получены аналитически. Однако в большинстве случаев их целесообразно решать графически (рис. 6.12). При исследовании устойчивости периодического решения уравнения (6.36), т.е. при определении существования автоколебаний в нелинейной системе с однозначной нелинейной статической характеристикой пользуются критерием Найквиста: периодическое решение с частотой w = w0 и амплитудой a = a 0 устойчиво, если при изменении частоты от нуля до бесконечности и положительном приращении амплитуды D a > 0 разность между числом положительных (сверху вниз) и отрицательных (снизу вверх) переходов фазовой характеристики линейной части системы yлч(w) через линию -p равна нулю в диапазоне частот, где Lлч(w)³-Lэ(w0, a 0+D a), и не равна нулю в диапазоне частот, где Lлч(w)³-Lэ(w0, a 0-D a). На рис. 6.10 показан пример определения периодических решений в нелинейной системе с ограничением. В такой системе имеются три периодических решения с частотами w01, w02 и w03, определяемыми в точках пересечения фазовой характеристики yлч(w) с линией -1800. Амплитуды периодического решения a 01, a 02 и a 03 определяются из условия (6.37) по логарифмическим амплитудным характеристикам нелинейного элемента -Lэ(w01, a), -Lэ(w02, a) и -Lэ(w03, a).
Рис. 6.10
Из трех решений, определенных на рис. 6.10, устойчивы два. Решение с частотой w = w01 и амплитудой a = a 01 устойчиво, так как в диапазоне частот 1, где Lлч(w)³-Lэ(w01, a 01+D a), фазовая характеристика yлч(w) не пересекает линию -1800, а в диапазоне частот 2, где Lлч(w)³-Lэ(w01, a 01-D a), фазовая характеристика yлч(w) один раз пересекает линию -1800. Решение с частотой w = w02 и амплитудой a = a 02 неустойчиво, так как в диапазоне частот, где Lлч(w)³-Lэ(w02, a 02+D a), фазовая характеристика yлч(w) один раз пересекает линию -1800. Высокочастотное периодическое решение с частотой w = w03 и амплитудой a = a 03 устойчиво, так как в диапазоне частот, где Lлч(w)³-Lэ(w03, a 03+D a), имеется один положительный и один отрицательный переход фазовой характеристики yлч(w) через линию -1800, а в диапазоне частот, где Lлч(w)³-Lэ(w03, a 03-D a), имеются два положительных и один отрицательный переход фазовой характеристики yлч(w) через линию -1800. В рассмотренной системе при малых по величине возмущениях установятся высокочастотные автоколебания с частотой w03 и амплитудой a 03, а при больших по величине возмущениях - низкочастотные автоколебания с частотой w01 и амплитудой a 01.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 531; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.49.66 (0.012 с.) |



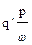 ] x, (6.21)
] x, (6.21)
 (6.23)
(6.23) ]}x = 0. (6.25)
]}x = 0. (6.25) (6.29)
(6.29) (6.30)
(6.30) . (6.33)
. (6.33) , взятой с обратным знаком (рис. 6.9). Если эти годографы не пересекаются, то режим автоколебаний в исследуемой системе не существует.
, взятой с обратным знаком (рис. 6.9). Если эти годографы не пересекаются, то режим автоколебаний в исследуемой системе не существует.




