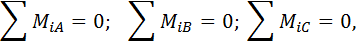Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частные случаи приведения произвольной пространственной системы сил к центруСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Случай I. Если главный вектор системы сил равен нулю и ее главный момент относительно центра приведения равен нулю, то силы взаимно уравновешиваются. Случай II. Если главный вектор системы сил равен нулю, а ее главный момент относительно центра приведения не равен нулю, то силы приводятся к паре сил. Момент этой пары сил равен главному моменту системы сил относительно центра приведения. В этом случае главные моменты системы сил относительно всех точек пространства геометрически равны. Случай III.
Случай IV. Если главный момент системы сил относительно центра приведения перпендикулярен к главному вектору, то силы приводятся к равнодействующей
Случай V. Если главный момент системы сил относительно центра приведения не перпендикулярен к главному вектору, то силы приводятся к двум скрещивающимся силам или к силовому винту (динаме), т.е. к совокупности силы и пары сил, плоскость которой перпендикулярна к силе. Приведение к двум скрещивающимся силам (рис. 147):
Уравнения равновесия различных систем сил Для сил, произвольно расположенных на плоскости, имеются два условия равновесия:
Два условия равновесия сил, произвольно расположенных на плоскости, можно выразить в виде системы трех уравнений:
Эти уравнения называются основными уравнениями равновесия плоской системы сил. Центр моментов и направление осей координат для этой системы уравнений можно выбирать произвольно. Для сил, произвольно расположенных в пространстве, соответствуют два условия равновесия:
Модули главного момента и главного вектора для рассматриваемой системы сил определяются по формулам:
Условия выполняются только при соответствующих им шести основных уравнения равновесия сил, расположенных произвольно в пространстве:
Первые три уравнения называют уравнениями моментов сил относительно осей координат, а последние три — уравнениями проекций сил на оси.
Формы уравнений равновесия плоской системы сил
Для сил, произвольно расположенных на плоскости, имеются два условия равновесия:
Два условия равновесия сил, произвольно расположенных на плоскости, можно выразить в виде системы трех уравнений:
Эти уравнения называются основными уравнениями равновесия плоской системы сил. Центр моментов и направление осей координат для этой системы уравнений можно выбирать произвольно. Существует и две другие системы трех уравнений системы сил.
При этом в системе ось u не должна быть перпендикулярна прямой проходящей через точки A и B. Так как главные моменты системы сил относительно двух центров равны нулю, то рассматриваемая система сил не приводится к паре сил. Проекция равнодействующей на любую ось равна сумме проекций составляющих сил, т.е.
где точки A, B, C не лежат на одной прямой. В этом случае силы не приводятся к паре сил, так как главные моменты сил относительно трех центров равны нулю. Силы не приводятся и к равнодействующей, так как если она существует, то линия ее действия не может пройти через три точки не лежащие на одной прямой. Таким образом, система сил не приводится ни к паре сил, ни к равнодействующей, а, следовательно, уравновешивается.
Центр параллельных сил При сложении двух параллельных сил две параллельные приводятся к одной силе — равнодействующей, линия действия которой направлена параллельно линиям действия сил. Равнодействующая приложена в точке делящей прямую, на расстояния обратно пропорциональные величинам сил.
Поскольку силу можно переносить по линии ее действия, то точка приложения равнодействующей не определена. Если силы повернуть на один и тот же угол и вновь произвести сложение сил, то получим другое направление линии действия равнодействующей. Точка пересечения этих двух линий равнодействующих может рассматриваться как точка приложения равнодействующей, не изменяющая своего положения при повороте всех сил одновременно на один и тот же угол. Такая точка называется центром параллельных сил.
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 2146; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.79.214 (0.008 с.) |


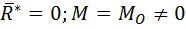

 Если главный вектор системы сил не равен нулю, а ее главный момент относительно центра приведения равен нулю, то силы приводятся к равнодействующей
Если главный вектор системы сил не равен нулю, а ее главный момент относительно центра приведения равен нулю, то силы приводятся к равнодействующей  , линия действия которой проходит через центр привидения.
, линия действия которой проходит через центр привидения. и
и  .
. .
.







 следовательно, предполагаемая равнодействующая
следовательно, предполагаемая равнодействующая  Таким образом, система сил не приводится ни к паре сил, ни к равнодействующей, а, следовательно, уравновешивается.
Таким образом, система сил не приводится ни к паре сил, ни к равнодействующей, а, следовательно, уравновешивается.