
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Плоская система произвольно расположенных силСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Цель работы: выявить степень усвоения у студентов теоретического материала по теме и навыков определения главных вектора и момента, а также опорных реакций балок.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Теорема Пуансо о переносе сил

А В А а В F3 В М
F1 = F2 = F3 Рис.4
Произвольная плоская система сил приводится к одной силе (главному вектору) и одному моменту (главному моменту системы сил) При изменении точки приведения величина главного вектора не изменится, но изменится величина главного момента, т.к. меняются расстояния от векторов-сил до новой точки приведения. С помощью теоремы Вариньона о моменте равнодействующей можно определить точку на плоскости, относительно которой главный момент равен нулю. Тогда произвольная плоская система сил может быть заменена одной силой, которую называют равнодействующей системы сил F∑. ПРАКТИЧЕСКАЯ ЧАСТЬ
Задание: Определить опорные реакции балки на двух опорах при действии вертикальных нагрузок. Использовать: Условия равновесия системы произвольных сил, теорему Вариньона, алгоритм решения РГР №2. Инструменты: транспортир, линейка, карандаш, резинка, калькулятор.
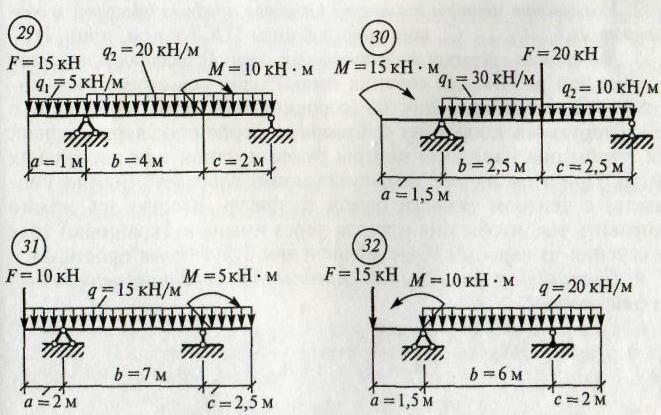
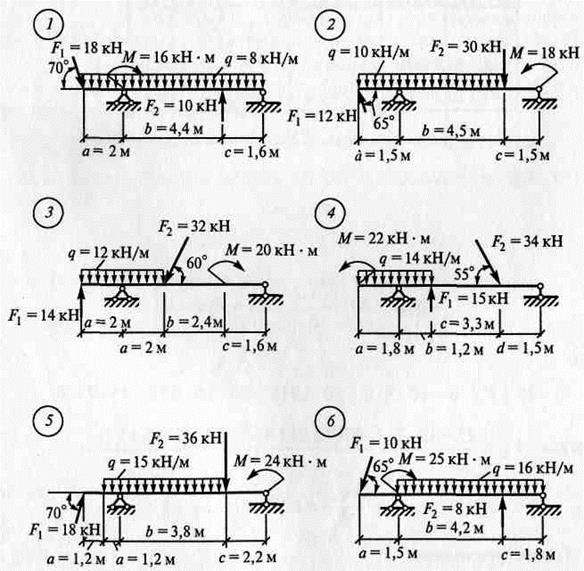
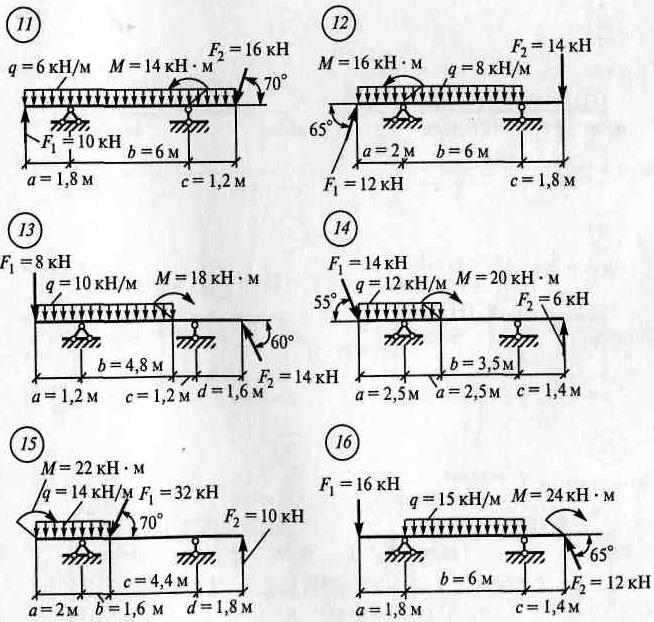
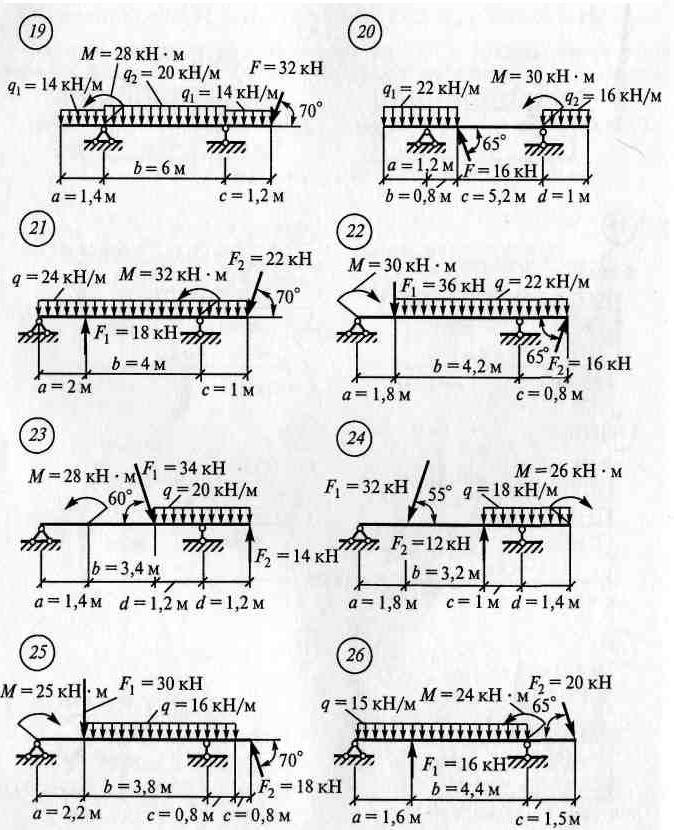
ЗАДАНИЯ ПО ВАРИАНТАМ Задача №1
Задача №2
Алгоритм решения задач: - выполнить схему нагружения балки - заменить равномерно-распределенную нагрузку (q) на равнодействующую - обозначить опоры (А, В …) - освободиться от опор и заменить их действие опорными реакциями - составить уравнения равновесия ∑ mА(Fк)= 0 ∑ mВ(Fk)= 0 - найти опорные реакции, выразив их из уравнений равновесия - выполнить проверку решением уравнения, неиспользованным в расчете опорных реакций ∑ Fkу = 0
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какую из форм уравнений равновесия целесообразно использовать при определении реакций в консольной балке? 2. Какую форму системы уравнений равновесия целесообразно использовать при определении реакций в опорах двухопорной балки и почему? 3. Главный вектор и главный момент системы сил равны нулю. Можно ли утверждать, что система сил находится в равновесии? 4. Зависят ли значение и направление момента силы относительно точки от взаимного расположения этой точки и линии действия силы? 5. Когда момент силы относительно точки равен нулю?
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №3 (РГР №3) Тема: Центр тяжести сечения
Цель работы: Закрепление теоретического материала и навыков расчета задач на определение центра тяжести составных плоских сечений с использованием таблиц сортамента листового и профильного проката. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Основными геометрическими характеристиками сечений плоских фигур являются: площадь сечения (A), статический момент (S), момент инерции (J), центр тяжести (С). Производными от основных характеристик являются момент сопротивления (W), радиус инерции (i). Многие характеристики зависят от выбора оси. Оси, проходящие через центр тяжести, называют центральными. Методы расчета центра тяжести: · метод симметрии · метод разделения на простые части · метод отрицательных площадей
ПРАКТИЧЕСКАЯ ЧАСТЬ Задание: 1) Определить положение центра тяжести плоского сечения, составленного из прокатных профилей и составных фигур. 2) Сделать вывод и указать положение центра тяжести на чертеже. Рекомендации к выполнению графической части задания: · Исходный чертеж (условие задачи) должен быть выполнен с предельной точностью в выбранном масштабе · Должны быть указаны все размеры, взятые из таблиц сортамента проката · Чем крупнее масштаб исходного чертежа, тем координаты центра тяжести сечения будут точнее При определении центра тяжести руководствоваться: 1. Центр тяжести прямоугольника лежит на пересечении диагоналей 2. Центр тяжести круга, квадрата, кольца совпадает с геометрическим центром 3. Центр тяжести треугольника лежит на пересечении его медиан Использовать: таблицы нормального сортамента проката, формулы определения центра тяжести простых сечений, методы разбиения и симметрии, алгоритм решения задач, контрольные вопросы самопроверки Замечание: при наличии одной оси симметрии, центр тяжести лежит на этой оси; при наличии двух осей симметрии центр тяжести совпадает с точкой пересечения этих осей. ЗАДАНИЯ ПО ВАРИАНТАМ Задача №1
Задача №2
Алгоритм решения задач: · y
xc= b/2
C h Yc= h/2 x b А = h . b R А = π R2 y C А = ½ h b h C y y= h/3 x C yc =4R/3π x=b/3 b Рис.5
· Выписываем характеристики простых сечений из сортамента (размеры, площадь сечения) · Выбираем систему координат Сложная фигура размещается на координатной плоскости таким образом, чтобы оси Х и У проходили по касательной к контуру чертежа. При наличии оси симметрии одну из координатных осей совместить с данной осью, а при наличии двух осей симметрии координатные оси совместить с данными осями симметрии
· Определяем координаты центров тяжести простых сечений, их площади и заносим данные в таблицу (ниже):
· Определяем координаты центра тяжести сложного тела по формулам:
Хс = ∑ Ак Хк / ∑ Ак = (А1 Х1 + А2 Х2 + А3 Х3 +…+ Ак Хк)/(А1 + А2 + А3 +…+ Ак) Ус = ∑ Ак Ук / ∑ Ак=(А1 у1 + А2 у2 + А3 у3 +…+ Ак ук)/ (А1 + А2 + А3 +…+ Ак) где А1, А2, А3,Ак – площади частей тела(простых сечений) Хк, Ук – координаты центров тяжести простых сечений · Указываем положение центра тяжести на чертеже. Точка С (Хс ;Ус ) · Выполняем проверку решения, изменив положение координатных осей Делаем выводы КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Где располагается центр тяжести тела, имеющего ось симметрии? 2. Где находится центр тяжести прямоугольника, круга, кольца? 3. Что называется статическим моментом площади сечения? В чем он измеряется? 4. Зависит ли статический момент площади от расположения площади относительно оси? 5. Как обозначается неравнополочный уголок? 6. Как обозначается швеллер? 7. Что обозначает № прокатной двутавровой балки? 8. Какие методы нахождения центра тяжести вы можете назвать? 9. Какие оси называют центральными осями? 10. Как определить геометрические характеристики прокатных профилей (уголка, швеллера, двутавра)?
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №4 (РГР №4)
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 3200; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |

 . Силу можно перенести параллельно линии её действия, при этом нужно добавить пару сил с моментом (М), равным произведению модуля силы (F1) на расстояние (а), на которое перенесена сила
. Силу можно перенести параллельно линии её действия, при этом нужно добавить пару сил с моментом (М), равным произведению модуля силы (F1) на расстояние (а), на которое перенесена сила
 F1 а F1 F2 F2
F1 а F1 F2 F2










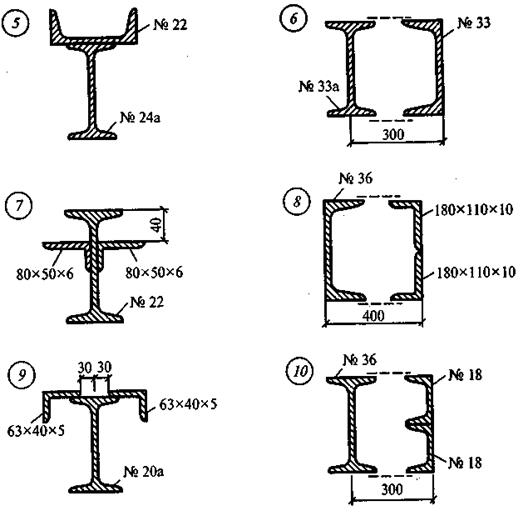
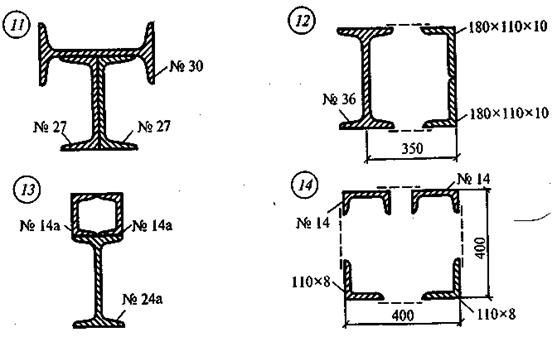









 Разбиваем однородную сложную фигуру на простые сечения, центры тяжести которых можно заранее определить
Разбиваем однородную сложную фигуру на простые сечения, центры тяжести которых можно заранее определить


