
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчетно-графическая работа №10 (ргр №10)Содержание книги
Поиск на нашем сайте Тема: Расчет на устойчивость сжатых стержней
Цель работы: Выявить степень закрепления у студентов теоретического материала и навыков расчета центрально-сжатых стержней
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Длинные стержни небольшого поперечного сечения под действием осевых сжимающих сил изгибаются и теряют равновесие. Равновесие считается устойчивым, если после снятия внешней силы стержень восстановит первоначальную форму. Если форма не восстанавливается, то говорят о потере устойчивости. Потеря устойчивости происходит в плоскости наименьшей жесткости, где момент инерции минимальный. На устойчивость влияет величина сжимающей силы, материал, длина стержня с учетом способа закрепления его концов (приведенная длина).
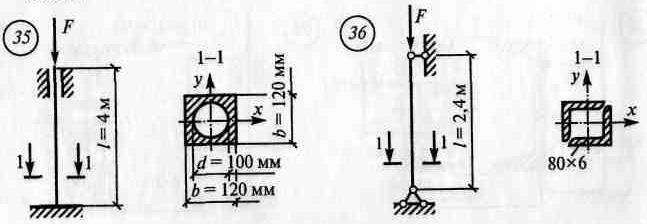
ПРАКТИЧЕСКАЯ ЧАСТЬ Использовать: условие гибкости стержня, условие устойчивости стержня, таблицы сортамента, алгоритм решения задач, контрольные вопросы самопроверки. Задача №1. Определить несущую способность стальной стойки при центральном сжатии. ВАРИАНТЫ ЗАДАНИЙ
Алгоритм решения задачи №1: 1. По СНиПу или справочнику определить расчетное сопротивление материала Ry Сетков В.И. «Сборник задач по технической механике» М.: «Академия», 2007г (приложение VIII)
2. Найти площадь поперечного сечения А, см2
3. Определить коэффициент продольного изгиба для чего: · Определить расчетную длину стержня Lef = μ L, м · Определить моменты инерции сечения относительно главных центральных осей Jx, Jy, см4 · Найти минимальный радиус инерции ______ imin= √ Jmin/ A, см · Определить гибкость стержня λ = μ L / imin
Коэффициент продольного изгиба φ определяется в зависимости от гибкости λ Сетков В.И. «Сборник задач по технической механике» М.: «Академия», 2007г (приложение IV)
4. Несущая способность определяется величиной допускаемого значения сжимающей силы N = Ry * φ * A, кн Задача №2. Подобрать сечение центрально-сжатой стойки, составленной из профилей проката. ЗАДАНИЯ ПО ВАРИАНТАМ
Алгоритм решения задачи №2: 1. Задаемся величиной коэффициента продольного изгиба φ = 0,6 ÷ 0,8 2. Определяем требуемую площадь сечения Ad ≥ F / Ry * φ, см2 3. По найденной площади определяем номера профилей проката, из которых состоит сечение, используя сортамент 4. Проверить устойчивость принятого сечения в следующем порядке: · Определить расчетную длину Lef = μ L, м · Определить моменты инерции сечения относительно главных центральных осей Jx, Jy, см4 Моменты инерции профилей проката относительно собственных осей определяются по сортаменту · Найти минимальный радиус инерции ______ imin= √ Jmin/ A,см · Определить наибольшую гибкость стержня λ мах = μ L / imin · Найти напряжения в сечении σ = F / А * φ ≤ Ry, кн/см2
Если это условие выполняется, значит устойчивость стойки обеспечена. Если условие не выполняется, то необходимо увеличить площадь стойки, приняв больший профиль и проверить устойчивость, добиваясь, чтобы напряжение было меньше расчетного сопротивления. Если напряжение намного меньше расчетного сопротивления, то такое сечение неэкономично, т.к. имеет большой запас прочности. Поэтому следует уменьшить площадь сечения стойки, добиваясь, чтобы недонапряжение не превышало 5%. Для каждой задачи выполнить схему нагружения и показать в выбранном масштабе сечение стойки.
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. От чего зависит значение коэффициента приведения длины стойки? 2. Что называется гибкостью стержня? 3. В чем заключается расчет сжатого стержня на устойчивость? 4. Требования, предъявляемые к конструкциям колонн при центральном сжатии? 5. От чего зависит коэффициент продольного изгиба?
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №11 (РГР№11) Тема: Расчет многопролетной статически-определимой разрезной (шарнирной) балки
Цель работы: Выявить степень закрепления у студентов теоретического материала, навыков расчета и построения эпюр для балочных конструкций
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Шарнирной балкой называется геометрически неизменяемая статически определимая, составленная из расположенных в определенной последовательности однопролетных и консольных простых балок, соединенных между собой шарнирами. Число промежуточных шарниров должно быть равно на три меньше числа опорных стержней. Простые балки делятся на три типа: 1. Основные – соединены с фундаментом, т.е. имеют 2 опоры 2. Промежуточные – имеют одну опору с фундаментом 3. Подвесные – не имеют опор с фундаментом Преимущество шарнирных балок по сравнению с неразрезными в том, что изгибающие моменты распределяются по длине балки рациональнее и требуется меньший расход материала. Правила размещения промежуточных шарниров: 1. Во всех пролетах, кроме любого одного может быть установлено по одному шарниру; 2. В одном пролете может быть установлено два шарнира, но такой пролет должен чередоваться с пролетом без шарниров, при этом в первом и последнем пролете установка шарниров не допускается.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Использовать: условие геометрической неизменяемости шарнирной балки, правила определения опорных реакций и построения эпюр, алгоритм решения задачи, контрольные вопросы самопроверки. Задача №1. Определить: · Геометрическую неизменяемость балки · Построить этажную схему · Построить эпюры Мизг и Q, предварительно определив опорные реакции отдельных простых балок ВАРИАНТЫ ЗАДАНИЙ
|
|
| Поделиться: |














 F3= F4
F3= F4



 F1 F2 q1 F3 F4
F1 F2 q1 F3 F4


















 1.
1.






 1,5м 2м 2м 1м 4м 1,5м 1м 1,5м 1м 2м
1,5м 2м 2м 1м 4м 1,5м 1м 1,5м 1м 2м F3= F4
F3= F4
















































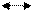


































 1м 3м 1м 4м 1м 1м 2м 1м
1м 3м 1м 4м 1м 1м 2м 1м

























