
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
По выполнению расчетно-графических работСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте ТЕХНИЧЕСКАЯ МЕХАНИКА Методические указания По выполнению расчетно-графических работ Для специальности 270103 Строительство и эксплуатация зданий и сооружений
Калининград УДК 62:744(076) З-12
Автор: Завьялов С.А.
Завьялов С.А. Техническая механика: методические указания по выполнению расчетно-графических работ – Калининград: ФГОУ СПО КГКГ, 2010. – 70 с.: табл., рис. Рассмотрено и согласовано на заседании ПЦК общепрофессиональных дисциплин протокол № 2 от 09.10.2010 г. Методические указания предназначены для студентов очной формы обучения по специальности 270103 Строительство и эксплуатация зданий и сооружений. В методических указаниях рассмотрены основные положения статики и сопротивления материалов, приведены варианты заданий и алгоритмы решений расчетно-графических работ в соответствии с рабочей программой дисциплины.
ФГОУ СПО КГКГ РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №1 (РГР №1) Тема: Плоская система сходящихся сил (ПССС)
Цель работы: Научиться определять равнодействующую системы сил, решать задачи на равновесие аналитическим и графическим способом, рационально выбирая координатные оси; определять реакции стержней.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
ПССС – система сил, линии действия которых пересекаются в одной точке.
F3
Рис.1
По следствию 3 аксиомы статики все силы системы можно переместить вдоль линии действия и все силы окажутся приложенными в одной точке. Равнодействующая сходящихся сил определяется с помощью параллелограмма или треугольника сил (4 аксиома)
F2 F1
Рис.2
Используя свойства векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил. Складывая последовательно силы, входящие в систему.
F4 F4 F3
Рис.3
Вектор равнодействующей силы соединяет начало 1 вектора с концом последнего. Силы можно вычерчивать в любом порядке – результат (направление и величина) равнодействующей при этом не меняется. Вектор равнодействующей силы направлен НАВСТРЕЧУ слагаемых векторов. ПРАКТИЧЕСКАЯ ЧАСТЬ КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Какая система сил называется сходящейся? 2. Назовите правила сложения двух сил, исходящих из одной точки? 3. Как найти проекцию вектора на ось? 4. Как геометрически найти равнодействующую плоской системы сходящихся сил (ПССС)? 5. В чем заключается геометрическое условие равновесия ПССС? 6. В чем заключается аналитическое условие равновесия ПССС? 7. Как рационально выбрать оси координат? 8. Сколько уравнений равновесия можно составить для плоской системы сходящихся сил (ПССС)? 9. Если значения усилия в стержне получилось отрицательным, что это nhзначит? 10. Какие требования предъявляются при построении силового многоугольника? РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №2 (РГР №2) Тема: Плоская система произвольно расположенных сил Цель работы: выявить степень усвоения у студентов теоретического материала по теме и навыков определения главных вектора и момента, а также опорных реакций балок.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Теорема Пуансо о переносе сил

А В А а В F3 В М
F1 = F2 = F3 Рис.4
Произвольная плоская система сил приводится к одной силе (главному вектору) и одному моменту (главному моменту системы сил) При изменении точки приведения величина главного вектора не изменится, но изменится величина главного момента, т.к. меняются расстояния от векторов-сил до новой точки приведения. С помощью теоремы Вариньона о моменте равнодействующей можно определить точку на плоскости, относительно которой главный момент равен нулю. Тогда произвольная плоская система сил может быть заменена одной силой, которую называют равнодействующей системы сил F∑. ПРАКТИЧЕСКАЯ ЧАСТЬ
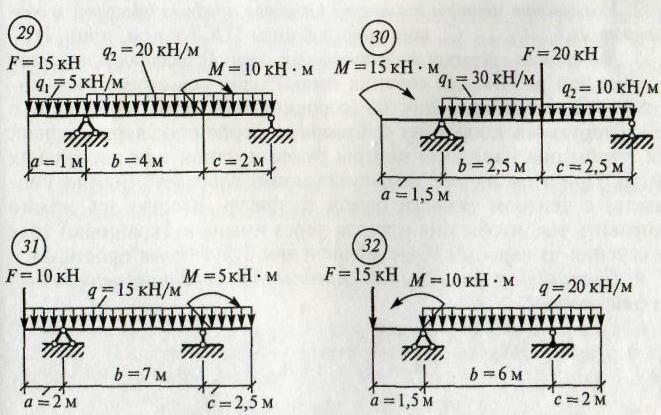
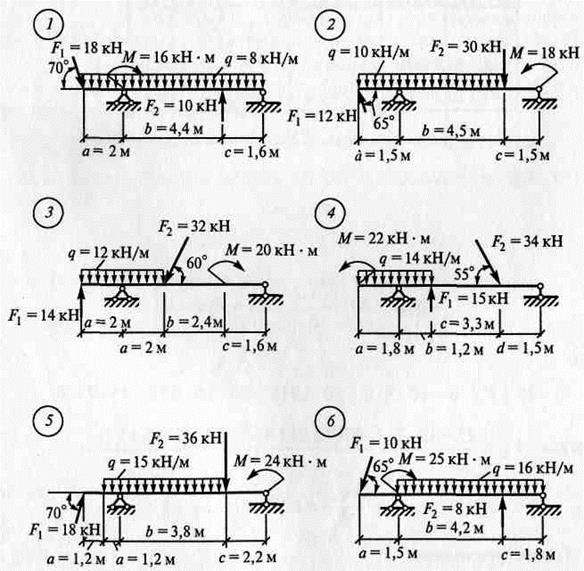
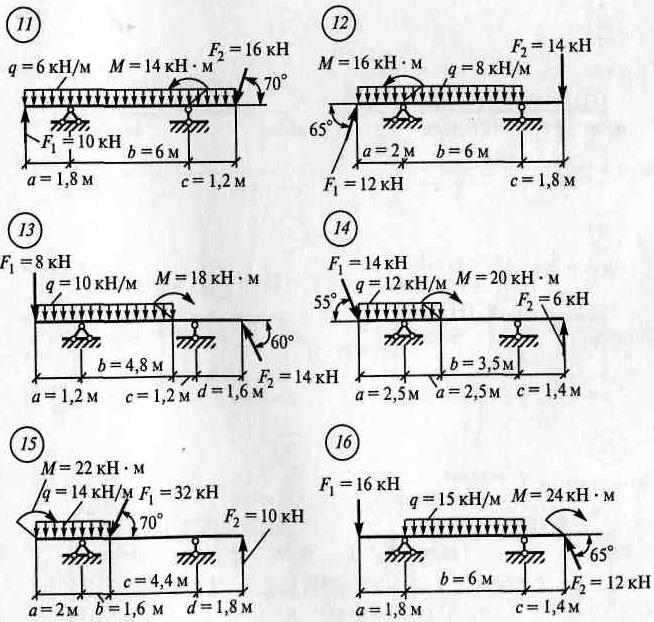
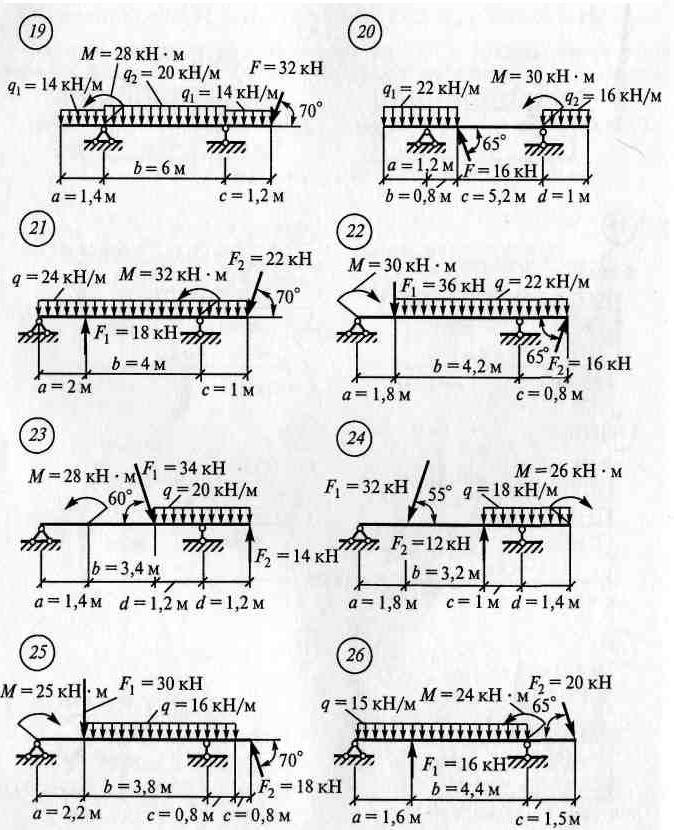
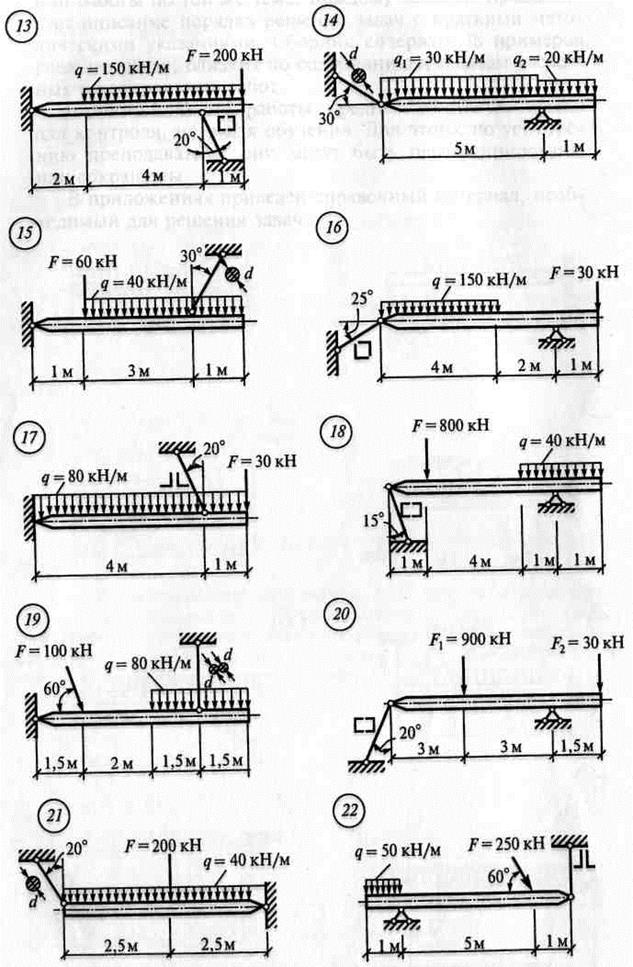
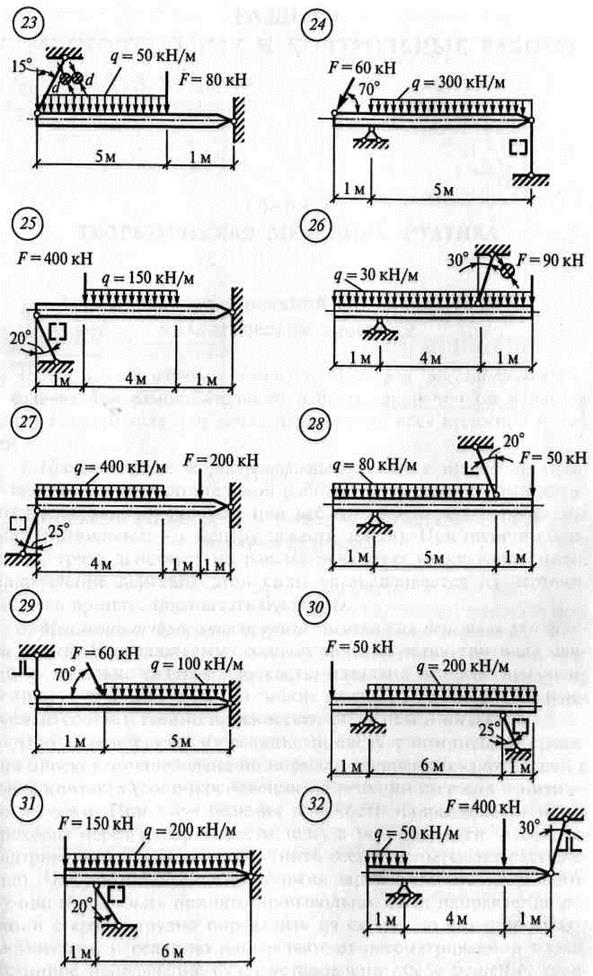
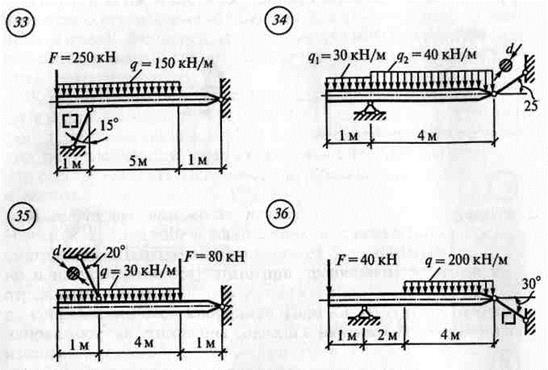
Задание: Определить опорные реакции балки на двух опорах при действии вертикальных нагрузок. Использовать: Условия равновесия системы произвольных сил, теорему Вариньона, алгоритм решения РГР №2. Инструменты: транспортир, линейка, карандаш, резинка, калькулятор.
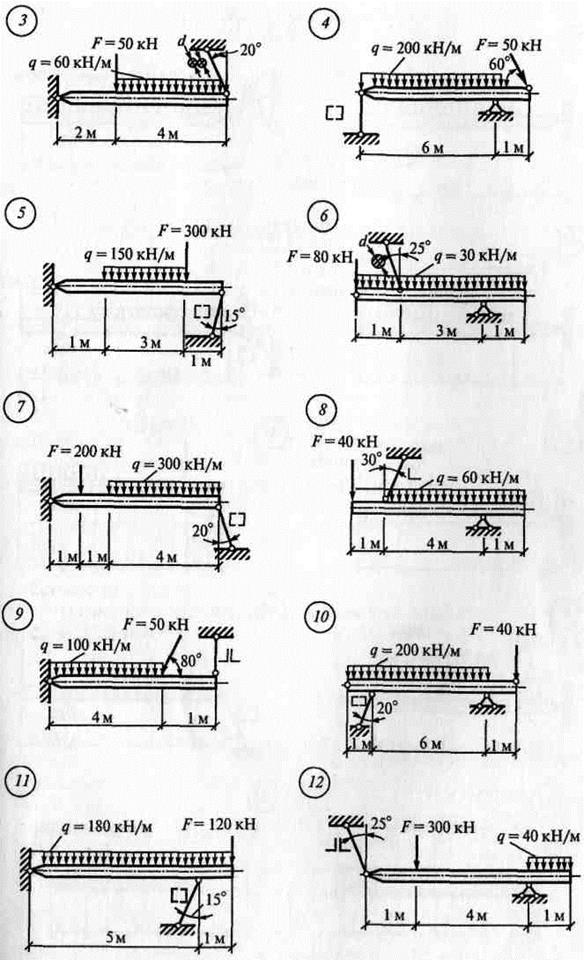
ЗАДАНИЯ ПО ВАРИАНТАМ Задача №1
Задача №2
Алгоритм решения задач: - выполнить схему нагружения балки - заменить равномерно-распределенную нагрузку (q) на равнодействующую - обозначить опоры (А, В …) - освободиться от опор и заменить их действие опорными реакциями - составить уравнения равновесия ∑ mА(Fк)= 0 ∑ mВ(Fk)= 0 - найти опорные реакции, выразив их из уравнений равновесия - выполнить проверку решением уравнения, неиспользованным в расчете опорных реакций ∑ Fkу = 0
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какую из форм уравнений равновесия целесообразно использовать при определении реакций в консольной балке? 2. Какую форму системы уравнений равновесия целесообразно использовать при определении реакций в опорах двухопорной балки и почему? 3. Главный вектор и главный момент системы сил равны нулю. Можно ли утверждать, что система сил находится в равновесии? 4. Зависят ли значение и направление момента силы относительно точки от взаимного расположения этой точки и линии действия силы? 5. Когда момент силы относительно точки равен нулю?
Тема: Центр тяжести сечения
Цель работы: Закрепление теоретического материала и навыков расчета задач на определение центра тяжести составных плоских сечений с использованием таблиц сортамента листового и профильного проката. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Основными геометрическими характеристиками сечений плоских фигур являются: площадь сечения (A), статический момент (S), момент инерции (J), центр тяжести (С). Производными от основных характеристик являются момент сопротивления (W), радиус инерции (i). Многие характеристики зависят от выбора оси. Оси, проходящие через центр тяжести, называют центральными. Методы расчета центра тяжести: · метод симметрии · метод разделения на простые части · метод отрицательных площадей
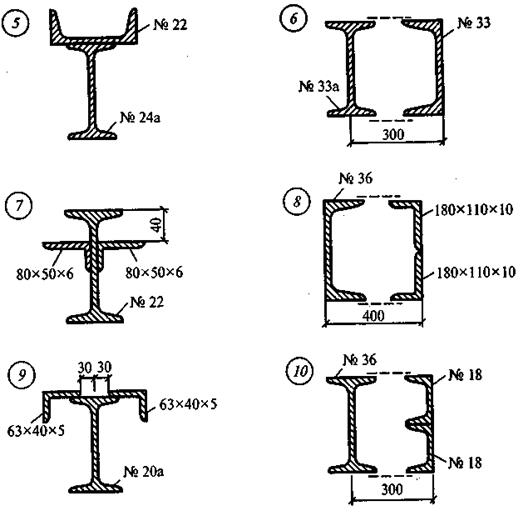
ПРАКТИЧЕСКАЯ ЧАСТЬ Задание: 1) Определить положение центра тяжести плоского сечения, составленного из прокатных профилей и составных фигур. 2) Сделать вывод и указать положение центра тяжести на чертеже. Рекомендации к выполнению графической части задания: · Исходный чертеж (условие задачи) должен быть выполнен с предельной точностью в выбранном масштабе · Должны быть указаны все размеры, взятые из таблиц сортамента проката · Чем крупнее масштаб исходного чертежа, тем координаты центра тяжести сечения будут точнее При определении центра тяжести руководствоваться: 1. Центр тяжести прямоугольника лежит на пересечении диагоналей 2. Центр тяжести круга, квадрата, кольца совпадает с геометрическим центром 3. Центр тяжести треугольника лежит на пересечении его медиан Использовать: таблицы нормального сортамента проката, формулы определения центра тяжести простых сечений, методы разбиения и симметрии, алгоритм решения задач, контрольные вопросы самопроверки Замечание: при наличии одной оси симметрии, центр тяжести лежит на этой оси; при наличии двух осей симметрии центр тяжести совпадает с точкой пересечения этих осей. ЗАДАНИЯ ПО ВАРИАНТАМ Задача №1
Задача №2
Алгоритм решения задач: · y
xc= b/2
C h Yc= h/2 x b А = h . b R А = π R2 y C А = ½ h b h C y y= h/3 x C yc =4R/3π x=b/3 b Рис.5
· Выписываем характеристики простых сечений из сортамента (размеры, площадь сечения) · Выбираем систему координат Сложная фигура размещается на координатной плоскости таким образом, чтобы оси Х и У проходили по касательной к контуру чертежа. При наличии оси симметрии одну из координатных осей совместить с данной осью, а при наличии двух осей симметрии координатные оси совместить с данными осями симметрии
· Определяем координаты центров тяжести простых сечений, их площади и заносим данные в таблицу (ниже):
· Определяем координаты центра тяжести сложного тела по формулам:
Хс = ∑ Ак Хк / ∑ Ак = (А1 Х1 + А2 Х2 + А3 Х3 +…+ Ак Хк)/(А1 + А2 + А3 +…+ Ак) Ус = ∑ Ак Ук / ∑ Ак=(А1 у1 + А2 у2 + А3 у3 +…+ Ак ук)/ (А1 + А2 + А3 +…+ Ак) где А1, А2, А3,Ак – площади частей тела(простых сечений) Хк, Ук – координаты центров тяжести простых сечений · Указываем положение центра тяжести на чертеже. Точка С (Хс ;Ус ) · Выполняем проверку решения, изменив положение координатных осей Делаем выводы КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Где располагается центр тяжести тела, имеющего ось симметрии? 2. Где находится центр тяжести прямоугольника, круга, кольца? 3. Что называется статическим моментом площади сечения? В чем он измеряется? 4. Зависит ли статический момент площади от расположения площади относительно оси? 5. Как обозначается неравнополочный уголок? 6. Как обозначается швеллер? 7. Что обозначает № прокатной двутавровой балки? 8. Какие методы нахождения центра тяжести вы можете назвать? 9. Какие оси называют центральными осями? 10. Как определить геометрические характеристики прокатных профилей (уголка, швеллера, двутавра)?
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №4 (РГР №4) ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Растяжением или сжатием называют вид нагружения, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор - продольная сила. Условно назначают знак продольной силы: + - растяжение; - - сжатие. Эпюрой продольной силы называется график распределения продольной силы вдоль оси бруса. Положительные значения сил откладывают от оси вверх, а отрицательные – вниз. Эпюра по контуру обводится толстой линией и заштриховывается поперек оси. При растяжении и сжатии действуют только нормальные напряжения, которые рассматриваются как силы, приходящиеся на единицу площади. Таким образом, направление и знак напряжения в сечении совпадают с направлением и знаком силы в сечении. Величина напряжений прямо пропорциональна продольной силе и обратно пропорциональна площади поперечного сечения. Эпюра напряжений строится и оформляется так же, как и эпюра продольных сил. Правило контроля при построении эпюр: в месте приложения внешней силы на эпюре должен быть скачок на величину этой силы. ПРАКТИЧЕСКАЯ ЧАСТЬ
Задание: Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить перемещение свободного конца бруса. Продольная сила F = 10кн (для всех вариантов)
Таблица 3
Исходные данные для выполнения задания
ВАРИАНТЫ ЗАДАНИЙ 1 – 8 9 – 16
F 2F 6F 2F 2F 5F a 3a 2a a b 2b 2b
17 – 24 25 – 32
А1= 4см2 А2 = 8см2 А1= 2см2 А2 = 4см2 А3= 6см2
5F 2F 3F 2F
c 2c 0,5c 0,5c d 1,5d 2 d 2d
Алгоритм выполнения расчетно-графической работы:
1) Брус разбить на отдельные участки, начиная от свободного конца. Границы участков определяются сечениями, где приложены внешние силы или где изменяются сечения бруса 2) Определить продольные силы (N), используя метод сечений 3) Построить эпюру продольных сил (N), пользуясь правилами построения · положительные значения продольных сил откладывают выше, а отрицательные – ниже нулевой линии для горизонтально расположенного бруса · на участках, свободных от нагрузки характер линии – прямая, параллельная нулевой линии · штриховка эпюры наносится перпендикулярно нулевой линии 4) Определить напряжения в поперечных сечениях бруса для каждого участка σ = N / A, кН/см2 5) Построить эпюру нормальных напряжений 6) Определить перемещение свободного конца бруса, как алгебраическую сумму абсолютных деформаций всех участков ΔL = N L0 / E А, см, где L0 – первоначальная длина каждого участка Е – модуль упругости (для стали Е = 2,1 .104 кн/см2) ΔL = ΔL 1+ ΔL2 + ΔL3 = N1 L1 / E А1 + N2 L2 / E А2 + N3 L3 / E А3
Вывод: Таким образом, свободный конец бруса перемещается вправо (влево) на …. см. Опасным является сечение бруса на участке …., где напряжения максимальны
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Какие силы в сопротивлении материалов считают внешними, а какие внутренними? 2. Какими методами определяют внешние силы? Как называют метод для определения внутренних сил? 3. Как обозначается и как определяется продольная сила в сечении? 4. Что называют механическим напряжением? 5. Какие напряжения возникают в поперечном сечении при действии продольных сил? 6. Какие деформации вызываются при действии продольной силы? 7. В каких единицах измеряется напряжение? 8. Какого характера напряжения возникают в поперечном сечении при растяжении или сжатии: нормальные или касательные? 9. Что характеризует модуль упругости материала? Какова единица измерения модуля упругости? 10. Как определяют абсолютное удлинение ступенчатого бруса, нагруженного несколькими силами?
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №5 (РГР №5) Тема: Расчеты на прочность при растяжении и сжатии Цель работы: Уметь проводить проектировочные и проверочные расчеты на прочность при растяжении и сжатии ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Расчеты ведутся по условиям прочности – неравенствам, выполнение которых гарантирует прочность детали. Для обеспечения прочности расчетное напряжение не должно превышать допускаемое напряжение: σ = N / A ≤ [σ ], кН/см2 расчетное напряжение зависит от нагрузки и размеров поперечного сечения, допускаемое - только от свойств материала и условий работы Существует три вида расчета на прочность: 1) Проектировочный расчет Задана расчетная схема и нагрузки; Материал или размеры конструкции подбираются: А ≥ N / [σ ] или σпред≥ N кзп / A 2) Проверочный расчет σ = N / A ≤ [σ ], кН/см2 3) Определение несущей способности (максимальной нагрузки) [N] = [σ ] А, кн ПРАКТИЧЕСКАЯ ЧАСТЬ Работа предполагает решение трех задач по вариантам. Задача №1. Прямой брус растянут силой N Таблица 4 Исходные данные для решения задачи №1
Материал Сталь Ст3 σт = 26 кн/см2; σв= 37 кн/см2 кзп =1,3. Определить размеры поперечного сечения бруса Алгоритм решения задачи №1: · Устанавливаем величину допускаемого напряжения [σ ]= σт / кзп · Определяем величину требуемой площади поперечного сечения · Подбираем необходимое сечение если сечение:
Задача №2. Проверить прочность сечения стержня из двух равнополочных уголков из стали марки ВСт3пс6 при действии осевой растягивающей силы N. Допускаемое напряжение [σ ] = 21 кн / см2 Таблица 5 Исходные данные для решения задачи №2
Алгоритм решения задачи №2: · Определяем по сортаменту площадь сечения заданного уголка Вычисляем площадь сечения стержня А = 2 Ауголка,см2 · Определяем нормальное напряжение и сравниваем с допускаемым напряжением · Делаем вывод
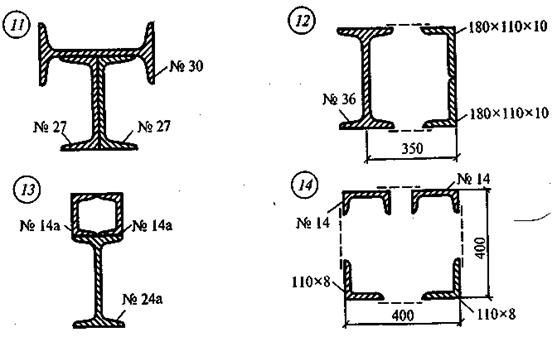
Задача №3. Подобрать сечение стержня-подвески (или колонны), поддерживающего брус Материал стержня: для фасонных профилей сталь С245 (Ry = 24 кн / см2), для круглого сечения – сталь арматурная горячекатаная класса А1 (Ry= 22,5 кн / см2) ЗАДАНИЯ ПО ВАРИАНТАМ
Алгоритм решения задачи №3: · Отбрасываем связи и заменяем их действие реакциями. По условию требуется рассчитать только стержень, поэтому показываем только усилия в стержне и не показываем реакции опоры · Определяем величину усилия в стержне N, составив уравнение равновесия ∑ Мв = 0 · Определяем требуемую площадь сечения стержня Атр ≥ N / Ry,см2 · По найденной площади подбираем требуемый профиль прокатной стали, используя сортамент, а диаметр стержня можно найти исходя из А = πd2/4, см2 · Проверяем прочность выбранного сечения σ = N / Aфакт ≤ Ry, кН/см2 · Делаем вывод (Например, «выбранное сечение из двух швеллеров №12 обеспечивает необходимую прочность») КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Что называется допускаемым напряжением? 2. Какие существуют виды расчета на прочность? 3. От чего зависит расчетное напряжение при растяжении? 4. Чем отличаются условия прочности при расчете на растяжение и расчете на сжатие? 5. Чем характеризуется 1 предельное состояние? 6. Что лежит в основе расчета по 1 предельному состоянию? 7. Каким методом пользуются при расчете строительных конструкций? 8. Каким методом пользуются при расчете машиностроительных конструкций и трубопроводов? 9. Что называется сортаментом? 10. Перечислите основные виды профильной стали? ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Сдвигом называется деформация, возникающая под действием двух близко расположенных противоположно направленных равных сил. При этом возникают касательные напряжения. Разрушение материала под их воздействием называется срезом. Касательные напряжения при срезе равны τ = F/ Aср , кН/см2 Аср= πd2 /4, см2 Условие прочности, элементов, работающих на срез имеет вид: τ ср = F / Aср ≤ [ τ ср] [ τ ср] = (0,7-0,8) [ σ ] где [ τ ср] - допускаемое касательное напряжение Часто одновременно со сдвигом происходит смятие боковой поверхности в месте контакта, где возникают сжимающие напряжения, называемые напряжениями смятия (σсм) Проверку элементов конструкции на смятие производят по формуле σсм=F / Aсм ≤ [ σсм ], кН/см2 где Асм – площадь смятия Асм= d . t (для заклепки), см2 [ σсм ] – допускаемое напряжение на смятие [ σсм ] = (1,8 – 2,2) [ σ ] Расчет сварных соединений Угловые швы рассчитываются на срез по наиболее опасной плоскости сечения шва, совпадающей с биссектрисой прямого угла треугольника (рис.2) и расчетной площадью сечения шва будет Аw = 0,7 к Lw, см2 где 0,7к – расчетная высота шва или расчетный катет шва Lw - длина шва,см Условие прочности сварного углового шва имеет вид: τw = F / 0,7 к Lw ≤ Rwf, кН/см2 где Rwf – расчетное сопротивление сварного углового шва при срезе Rwf = 18 кн/см2 для стали Ст3 При проектировании сварных соединений следует обеспечивать условие равнопрочности, т.е. допускаемая нагрузка на шов и основной свариваемый материал должны быть одинаковы. Fw доп = Fдоп = А Rу, кн Тогда длина стыкового равнопрочного шва будет равна Lw = Ry b / Rwy, см Необходимая длина углового шва ΣLw ≥ Fдоп / 0,7к Rwf ПРАКТИЧЕСКАЯ ЧАСТЬ КОНТРОЛЬНЫЕ ВОПРОСЫ
1. При действии каких сил возникает деформация сдвига? 2. Какие напряжения возникают при деформации сдвига? 3. Что называется смятием? 4. Какие напряжения возникают при смятии? 5. Как направлены лобовые швы нахлесточного соединения по отношению к действующей нагрузке? 6. Как направлены фланговые швы нахлесточного соединения по отношению к действующей нагрузке? 7. Что такое катет шва? От чего он зависит? 8. Что такое равнопрочность сварного соединения? РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №7 (РГР №7) Тема: Геометрические характеристики плоских сечений Цель работы: научиться определять главные центральные моменты инерции для сечений, имеющих ось симметрии
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ · Момент инерции сложной фигуры является суммой моментов инерции частей, на которые её разбивают · Моменты инерции вырезов и отверстий имеют отрицательную величину · Моменты инерции частей, чьи главные оси не совпадают с центральными осями сечения в целом, пересчитывают с помощью формулы для моментов инерции относительно параллельных осей Jх = Jх0 + А а2, где а – расстояние между осями 0х и 0х0 · Моменты инерции стандартных профилей определяются по сортаментам. Для полосовой стали использовать формулы для прямоугольника
ПРАКТИЧЕСКАЯ ЧАСТЬ Задача №1. Определить геометрические характеристики плоских фигур.
d х0 h1 a H h3 h2 х h1
b1 b2
Рис.8
Таблица 8
Исходные данные для решения задачи №1
Задача №2. Определить центральные моменты инерции сечения в соответствии с вариантом расчетно-графической работы №3 «Центр тяжести». Алгоритм решения задач: 1) Определяем геометрические характеристики простых сечений (круга, прямоугольника) для круглого сечения А= πd2/4, см2 Jх = Jу = πd4/64,см4 для прямоугольного сечения А= b h, см2 Jх = b h3/ 12,см4 Jy = b3 h/ 12,см4 Для сечений, составленных из прокатного профиля, геометрические характеристики определяем по сортаменту. 2) Устанавливаем координаты центров тяжести простых фигур, для чего проведем центральные оси для каждой простой фигуры 3) Проводим главные центральные оси, которые проходят через центр тяжести всего сечения 4) Определяем главные моменты инерции сечения, как сумму моментов инерции простых фигур используя формулу моментов инерции относительно параллельных осей Примеры определения главных моментов инерции сечения приведены на стр.140-143 Сетков В.И. «Сборник задач по технической механике» М.: «Академия», 2007г
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Какие оси называются центральными? 2. Какие оси называются главными центральными? 3. В чем измеряется момент инерции сечения? 4. Как обозначается балка двутавровая? 5. Что обозначает № швеллера? 6. Диаметр сплошного вала увеличили в 2 раза. Во сколько раз увеличится осевой момент инерции? ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Эпюры поперечных сил и изгибающих моментов можно строить, предварительно разбив балку на отдельные участки нагружения и составляя уравнения, выражающие изменения Q и M по участкам. Принятые знаки поперечных сил и изгибающих моментов:

F Рис.9
Поперечная сила считается положительной в сечении, если она стремится развернуть сечение по часовой стрелке; если против, - отрицательной. Если действующие на участке внешние силы стремятся изогнуть балку выпуклостью вниз, то изгибающий момент считается положительным, если наоборот –выпуклостью вверх- отрицательным.
m Mx m Mx -- «минус» + «плюс»
Рис.10
Рис.11 ПРАКТИЧЕСКАЯ ЧАСТЬ
Задание: Используя правила построения эпюр поперечных сил и изгибающих моментов и результаты решения задачи №1 расчетно-графической работы №2, построить эпюры Мx и Qy.
Алгоритм выполнения задания: 1. Обозначить характерные сечения (точки) балки и значения опорных реакций 2. Построить эпюру поперечных сил Для этого: - определить значения поперечных сил в характерных точках как сумму проекций всех сил, находящихся только слева (или только справа) от сечения - установить знаки - в точках приложения сил, в том числе опорных реакций определить два значения поперечной силы Qлев, Qправ - отложить в выбранном масштабе от нулевой линии найденные значения и соединить их прямыми линиями 3. Построить эпюру изгибающих моментов Для этого: - определяем Мх в характерных сечениях - устанавливаем знаки - в сечениях, соответствующим точкам приложения сосредоточенных моментов необходимо определить два значения изгибающего момента (чуть левее и чуть правее рассматриваемой точки) Млев, Мправ В точках приложения сил определяется одно значение М - отложить в выбранном масштабе от нулевой линии найденные значения и соединить по следующим правилам: o Если нет распределенной нагрузки, то прямой линией o Если есть распределенная нагрузка, то соединение по параболе
|



 F1 у F2
F1 у F2

 F4 х
F4 х





 F1 F1 F∑ F2
F1 F1 F∑ F2 
 F2 F∑
F2 F∑
 Образуется силовой многоугольник. F2
Образуется силовой многоугольник. F2



 F1 F2 F1 F3 F∑
F1 F2 F1 F3 F∑  . Силу можно перенести параллельно линии её действия, при этом нужно добавить пару сил с моментом (М), равным произведению модуля силы (F1) на расстояние (а), на которое перенесена сила
. Силу можно перенести параллельно линии её действия, при этом нужно добавить пару сил с моментом (М), равным произведению модуля силы (F1) на расстояние (а), на которое перенесена сила
 F1 а F1 F2 F2
F1 а F1 F2 F2



















 Разбиваем однородную сложную фигуру на простые сечения, центры тяжести которых можно заранее определить
Разбиваем однородную сложную фигуру на простые сечения, центры тяжести которых можно заранее определить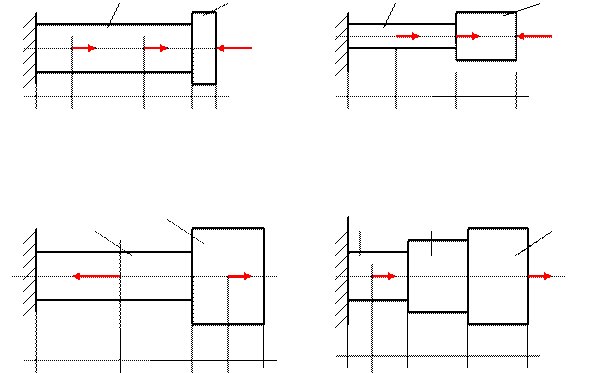 А1= 3см2 А2 = 5см2 А1= 2см2 А2 = 6см2
А1= 3см2 А2 = 5см2 А1= 2см2 А2 = 6см2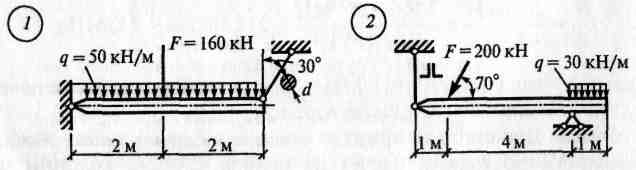
 у D B
у D B
 F F
F F

 Q + «плюс» Q
Q + «плюс» Q



 F
F

 Q -- «минус» Q
Q -- «минус» Q







