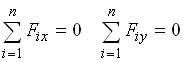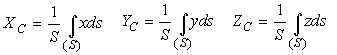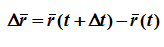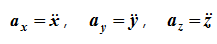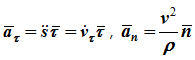Системы сходящихся сил. Теорема о существовании равнодействующей. Условия равновесия.

СТАТИКА

Аксиомы статики

Аксиома 1. Две силы, действующие на абсолютно твердое тело уравновешива-ются только тогда, когда они равны по величине и направлены по од-ной прямой в противоположные стороны (рис. 1.2).

 

Рис. 1.2 Рис. 1.3

Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изме-нится, если прибавить к ней или отнять от нее уравновешенную сис-тему сил (рис. 1.3).

Следствие из аксиомы 1 и 2. Действие силы на абсолютно твердое тело (АТТ) не изменится, если точку приложения этой силы перенести по ли-нии ее действия. Пусть на тело в точке А действует сила (рис. 1.4). Добавим в точке В, выбранной произвольно на линии действия си-лы , уравновешенную систему сил и равных по абсолютной величине и направленных по линии ее действия. На основании аксиомы 1 силы и будут уравновешены и их можно отбросить (аксиома 2). В результате получим силу = , но приложенную не в точке А, а в точке В. Отсюда следует, что сила, приложенная к АТТ, есть вектор скользящий.

Рис. 1.4 Рис. 1.5 Рис. 1.6

Аксиома 3 Равнодействующая двух сил, приложенных к АТТ в одной точке, равна

их геометрической сумме , т.е. выражается по моду-лю и направлению диагональю

параллелограмма,построенного на этих силах (рис. 1.5).

Аксиома 4 Всякому действию одного тела на другое соответствует равное по величине,

но противоположное по направлению противодействие. Действие и противодействие-это силы,

приложенные к двум раз-личным телам, поэтому они не уравновешиваются (рис. 1.6).

Аксиома 5 Если деформируемое тело под действием системы сил находится в

равновесии, то при отвердевании его равновесие сохраняется.

Под действием сил тело D находится в равновесии. Если трос CB заменить стержнем,

то равновесие не нарушится, равновесие не нарушится и в том случае, если трос BD

за-менить стержнем, если же стержень АВ заменить тросом - равновесие нарушится

(рис. 1.7).

Рис.1.7

 

Связи и их реакции

 

Системы сходящихся сил. Теорема о существовании равнодействующей. Условия равновесия.

Система сил называется сходящейся, если линии действия всех сил системы пересекаются в одной точке.

Пусть система сходящихся сил (F₁, F₂,...,F_n) приложена к твердому телу (рис. 12, a).

Согласно следствию второй аксиомы, переносим все силы системы в точку пересечения линий действия A и получаем систему сил, приложенных в одной точке (рис. 12, b). По аксиоме параллелограмма сил, начиная с сил F₁ и F₂, последовательно складываем силы, добавляя каждый раз к полученной сумме по одной силе системы. Дойдя до последней силы F_n, выясняем, что система сил (рис. 12, b) эквивалентна одной силе или равнодействующей R^* (рис. 12, c), равной геометрической сумме сил системы.

Таким образом, система сходящихся сил приводится к равнодействующей (эквивалентна равнодействующей), которая равна геометрической сумме сил системы и приложена в точке пересечения линий действия сил:

(F1, F2,...,Fn) ~ R^*; R^* = F1 + F2 +... + Fn

Для равновесия твердого тела под действием системы сходящихся сил необходимо и достаточно, чтобы геометрическая сумма всех сил системы была равна нулю:

для равновесия твердого тела под действием системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник системы был замкнутым.

Для равновесия твердого тела под действием системы сходящихся сил необходимо и достаточно, чтобы суммы проекций сил системы на оси координат были равны нулю.

 

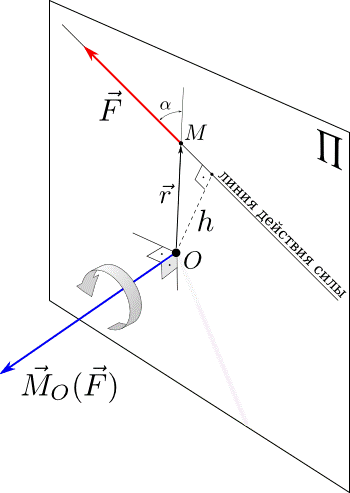
Момент силы относительно центра

Момент силы относительно точки О - это вектор, модуль которого равен произведению модуля силы на плечо - кратчайшее расстояние от точки О до линии действия силы. Направление вектора момента силы перпендикулярно плоскости, проходящей через точку и линию действия силы, так, что глядя по направлению вектора момента, вращение, совершаемое силой вокруг точки О, происходит по часовой стрелке.

Если известен радиус-вектор r ⃗ точки приложения силы F ⃗ относительно точки О, то момент этой силы относительно О выражается следующим образом:

M ⃗ _O (F ⃗) = r ⃗× F ⃗.

Действительно, модуль этого векторного произведения:

| M ⃗ _O | = | r ⃗× F ⃗| = | r ⃗|| F ⃗|sin α.

В соответствии с рисунком | r ⃗|sin α = h, поэтому:

| M ⃗ _O | = | F ⃗| h.

 

Пара сил. Теорема о сумме моментов сил пары относительно произв. Центра.

Теоремы о парах.

 

Теорема 1. Две пары, лежащие в одной плоскости, можно заменить одной парой, лежащей в той же плоскости, с моментом, равным сумме моментов данных двух пар. Для док–ва рассмотрим две пары (F₁, F`<sub>1</sub>) и (F<sub>2</sub>, F`₂) (рис. 3.9) и перенесем точки приложения всех сил вдоль линий их действия в точки А и В соответственно. Складывая силы по аксиоме 3, получим R=F₁+F₂ и R'=F`<sub>1</sub>+F`₂, но F'₁=–F₁ и F`<sub>2</sub>=–F<sub>2</sub>. Следовательно, R=–R', т. е. силы R и R' образуют пару. Момент этой пары: М=М(R, R')=ВАxR=BAx(F<sub>1</sub>+F<sub>2</sub>)=ВАxF<sub>1</sub>+ВАxF<sub>2</sub>. (3.14). При переносе сил, составляющих пару, вдоль линий их действия ни плечо, ни направление вращения пары не меняются, следовательно, не меняется и момент пары. Зна­чит, ВАхF<sub>1</sub>=M(F<sub>1</sub>, F'<sub>1</sub>)=M<sub>1</sub>, ВАxF<sub>2</sub>=M(F<sub>2</sub>, f`₂)=M₂, и формула (З.14) примет вид M=M₁+M₂, (3.15) ч.т.д. Сделаем два замечания. 1. Линии действия сил, составляющих пары, могут оказаться параллельными. Теорема остается справедливой и в этом случае. 2. После сложения может получиться, что М(R,R')=0; на основании замечания1 из этого следует, что сово­купность двух пар (F₁, F`<sub>1</sub>, F<sub>2</sub>, F`₂)~0.

 

Теорема 2. Две пары, имеющие равные моменты, эквивалентны. Пусть на тело в плоскости I действует пара (F₁,F`<sub>1</sub>) с моментом M<sub>1</sub>. Покажем, что эту пару можно заменить другой парой (F<sub>2</sub>, F`₂), расположенной в плоскости II, если только ее момент М₂ равен М₁. Заметим, что пло­скости I и II должны быть параллельны, в частности, они могут совпадать. Действительно, из параллельности моментов M₁, и М₂ следует, что плоскости действия пар, перпендикулярные моментам, также параллельны. Введем в рассмотрение новую пару (F₃, F`<sub>3</sub>) и приложим ее вместе с парой (F<sub>2</sub>, F`₂) к телу, расположив обе пары в плоскости II. Для этого согласно аксиоме 2 нужно подобрать пару (F₃, F`<sub>3</sub>) с мо­ментом М<sub>3</sub> так, чтобы приложенная система сил (F<sub>2</sub>, F`₂, F₃, F`<sub>3</sub>) была уравновешена. Положим F<sub>3</sub>=–F`₁ и F`<sub>3</sub>=–F<sub>1</sub> и совместим точки при­ложения этих сил с проекциями А<sub>1</sub> и B<sub>1</sub> точек А и В на плоскость II (см. рис. 3.10). В соответствии с построением будем иметь: М<sub>3</sub>=–M<sub>1</sub> или, учитывая, что М<sub>1</sub>=М<sub>2</sub>, М<sub>2</sub>+М<sub>3</sub> = 0, получим (F<sub>2</sub>, F`₂, F₃, F`<sub>3</sub>)~0. Т.о., пары (F<sub>2</sub>, F`₂) и (F₃, F`<sub>3</sub>) взаимно уравновешены и присоединение их к телу не нару­шает его состояния (аксиома 2), так что (F<sub>1</sub>, F`₁)~(F₁, F`<sub>1</sub>, F<sub>2</sub>, F`₂, F₃, F`<sub>3</sub>). (3.16). С другой стороны, силы F<sub>1</sub> и F<sub>3</sub>, а также F`₁ и F`<sub>3</sub> можно сло­жить по правилу сложения параллельных сил, направленных в одну сторону. Они равны по модулю, поэтому их рав­нодействующие R и R' должны быть приложены в точке пересече­ния диагоналей прямоугольника ABB<sub>1</sub>A<sub>1</sub>, кроме того, они равны по модулю и направлены в проти­воположные стороны. Это означает, что они составляют систему, экви­валентную нулю. Итак, (F<sub>1</sub>, F`₁, F₃, F`<sub>3</sub>)~(R, R')~0. Теперь можем записать (F<sub>1</sub>, F`₁, F₂, F`<sub>2</sub>, F<sub>3</sub>,F`₃)~(F₂, F`<sub>2</sub>).(3.17). Сравнивая соотношения (3.16) и (3.17), получим (F<sub>1</sub>, F`₁)~(F₂, F`₂), ч.т.д. Из этой теоремы следует, что пару сил можно перемещать и поворачивать в плоскости ее действия, переносить в параллельную плоскость; в паре можно менять одновременно силы и плечо, сохраняя лишь направление вращения пары и модуль ее момента (F₁h₁=F₂h₂).

Теорема 3. Две пары, лежащие в пересекающихся плоскостях, эквивалентны одной паре, момент которой равен сумме моментов двух данных пар. Пусть пары (F₁, F`<sub>1</sub>) и (F<sub>2</sub>, F`₂) расположены в пересекающихся плоскостях I и II соответственно. Пользуясь следствием теоремы 2, приведем обе пары к плечу АВ (рис. 3.11), расположенному на ли­нии пересечения плоскостей I и II. Обозначим трансформированные пары через (Q₁, Q`<sub>1</sub>) и (Q<sub>2</sub>, Q`₂). При этом должны выполняться ра­венства: M₁=M(Q₁, Q`<sub>1</sub>)=M(F<sub>1</sub>, F`₁) и M₂=M(Q₂, Q`<sub>2</sub>)=M(F<sub>2</sub>, F`₂). Сложим по аксиоме 3 силы, приложенные в точках А и В соот­ветственно. Тогда получим R=Q₁+Q₂ и R'=Q`<sub>1</sub>+Q`₂. Учиты­вая, что Q`<sub>1</sub>=–Q<sub>1</sub> и Q`₂= –Q₂, получим: R=–R'. Т.о., мы доказали, что система двух пар эквивалентна одной паре (R, R'). Найдем момент М этой пары. М(R, R')=ВАxR, но R=Q₁+Q₂ и М(R, R')=ВАх(Q₁+Q₂)=BAxQ₁+BAxQ₂=M(Q₁, Q`<sub>1</sub>)+M(Q<sub>2</sub>, Q`₂)=M(F₁, F'₁)+M(F₂, F`₂), или M=M₁+M₂, т. е. теорема доказана.

Вывод: момент пары является свободным вектором и полностью оп­ределяет действие пары на абсолютно твердое тело. Для деформируемых тел теория пар неприменима.

 

Основная теорема статики

Главным вектором системы сил называют вектор, равный сумме всех сил системы:

Главным моментом системы сил относительно центра называют вектор, равный сумме моментов всех сил системы относительно центра:

Сформулируем основную теорему статики.

Произвольная система сил, приложенная к твердому телу, эквивалентна одной силе, приложенной в центре приведения и равной главному вектору, и одной паре сил, момент которой равен главному моменту относительно центра приведения:

Докажем теорему. Пусть к твердому телу приложена произвольная система сил (F₁, F₂,..., F_n). Какую либо точку тела выберем за центр приведения и обозначим буквой O. Следуя лемме, силы системы переносим в эту точку и получаем систему пар сил и пучок сил в центре приведения. Складывая все силы пучка и пары сил, получаем одну силу в центре приведения и одну пару сил. Силы пучка по величине и направлению равны силам исходной системы, поэтому полученная сила равна главному вектору системы R. Моменты пар равны моментам соответствующих сил относительно центра O, поэтому момент полученной пары сил (F,F') равен главному моменту системы M_O. Теорема доказана.

Заметим, что при параллельном переносе сил к центру приведения не изменились ни модули, ни направления сил, поэтому главный вектор не зависит от выбора центра приведения. Главный вектор является инвариантом (неизменной величиной) данной системы сил. В отличие от главного вектора, главный момент зависит от выбранного центра приведения и не является инвариантом.

 

Для равновесия твердого тела под действием плоской системы сил необходимо и достаточно, чтобы равнялись нулю две суммы проекций сил на оси координат и сумма алгебраических моментов всех сил относительно любой точки плоскости.

Для равновесия твердого тела под действием плоской системы сил необходимо и достаточно, чтобы равнялись нулю три суммы моментов сил системы относительно трех точек плоскости, не лежащих на одной прямой:

Для равновесия твердого тела под действием плоской системы сил необходимо и достаточно, чтобы равнялись нулю две суммы моментов сил системы относительно двух точек плоскости и сумма проекций сил системы на ось, не перпендикулярную прямой, соединяющей эти точки:

 

Метод интегрирования.

Выражаем координаты центра тяжести неоднородного тела следующим образом:

Для однородных тел (центры тяжести объема, поверхности, площади и линии) эти координаты мы находим по формулам:

dv, ds, dl - элементарные объемы, площади и отрезки, x,y,z - координаты этих элементарных объемов, площадей и отрезков, а P для неоднородного тела вычисляется как

Метод симметрии.

 

 

Метод применяется только для однородных тел. Опуская несложные доказательства, сформулируем три правила метода.

1. Если тело имеет плоскость симметрии, то центр тяжести тела лежит в этой плоскости.

2. Если тело имеет ось симметрии, то центр тяжести тела находится на этой оси.

3. Если тело имеет центр симметрии, то центр тяжести тела находится в этой точке.

Используя правила, определим положение центра тяжести однородного цилиндра высотой H.

Рассечем цилиндр по диаметру плоскостью П₁, которая является первой плоскостью симметрии цилиндра (рис. 43). Рассекая цилиндр по другому диаметру второй плоскостью симметрии П₂, найдем ось симметрии AA цилиндра, являющуюся линией пересечения двух плоскостей симметрии и совпадающую с осью цилиндра. Наконец, рассекая цилиндр пополам плоскостью П₃, перпендикулярной оси цилиндра, найдем центр симметрии C, находящийся в точке пересечения плоскости симметрии П₃ с осью симметрии AA. Таким образом, центр тяжести однородного цилиндра находится на оси цилиндра на высоте H/2 от основания (рис. 43).

Метод разбиения.

Он применяется, когда однородное тело можно разбить на части, положения центров тяжести которых известны или легко определяются. В неоднородном теле эти части должны иметь еще и одинаковый удельный вес во всех их точках. После разбиения положение центра тяжести всего тела находят, используя дискретные формулы для определения координат центра тяжести.

Применим метод для плоского однородного треугольника. Разобьем треугольник ABD на узкие полоски, параллельные стороне AD (рис. 44). Центры тяжести отрезков линий, за которые в пределе приняты полоски, будут лежать на медиане BC₁, там же должен лежать и центр тяжести всего треугольника. Аналогичные результаты получатся для медианы DC₂, когда полоски параллельны стороне AB треугольника. Следовательно, точка C пересечения медиан будет центром тяжести всего треугольника. Причем из геометрии известно, что CC₁ = BC₁ / 3, а CC₂ = DC₂ / 3.

КИНЕМАТИКА

1. Способы задания движения точки

При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.

При координатном способе задания движения задаются координаты точки как функции времени:

Это и параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них t.

При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t). Этим способом удобно пользоваться, если траектория точки заранее известна.

 

2. Определение скорости и ускорения точки при векторном способе задания движения.

Рассмотрим перемещение точки за малый промежуток времени Δt:

тогда

средняя скорость точки за промежуток времени Dt. Скорость точки в данный момент времени

 

Среднее ускорение

характеризует изменение вектора скорости за малый промежуток времени Δt. Ускорение точки в данный момент времени

 

Координатном

Связь векторного способа задания движения и координатного дается соотношением

Из определения скорости

Проекции скорости на оси координат равны производным соответствующих координат по времени:

Модуль и направление скорости определяются выражениями

Из определения ускорения

Проекции ускорения на оси координат равны вторым производным соответствующих координат по времени

Модуль и направление ускорения определяются выражениями

Естественном

Из определения скорости точки

Где

- единичный вектор касательной, тогда

Алгебраическая скорость – это проекция вектора скорости на касательную, равная производной от дуговой координаты по времени. Если производная положительна, то точка движется в положительном направлении отсчета дуговой координаты.

Из определения ускорения

поскольку τ - переменный по направлению вектор, то:

Производная

определяется только свойствами траектории в окрестности данной точки, при этом

n - единичный вектор главной нормали,

ρ - радиус кривизны траектории в данной точке.

Таким образом,

т.е. вектор ускорения раскладывается на две составляющие - касательное и нормальное ускорения:

Здесь:

- алгебраическое значение касательного ускорения (проекция вектора ускорения на касательную) характеризует изменение скорости по величине;

– нормальное ускорение (проекция вектора ускорения на главную нормаль) характеризует изменение скорости по направлению. Вектор ускорения всегда лежит в соприкасающейся плоскости и проекция ускорения на бинормаль равна нулю (a_b=0).

Движение точки ускоренное, если знаки проекций векторов скорости и ускорения на касательную совпадают.

ДИНАМИКА

1. Законы динамики
2. Основное уравнение динамики. Дифференциальные уравнения движения м.т. в проекциях на декартовые и естественные оси. Первая и вторая задача динамики.
3. Основное уравнение динамики относительного движения. Инерциальная система отсчета.
4. Прямолинейные колебания м.т. Классификация сил, действующих на м.т. при колебании.
5. Свободные колебания в среде без сопротивления.
6. Свободные колебания в среде с сопротивлением
7. Механическая система. Диффуры движения механической системы.
8. Центр масс, формулы.
9. Теорема о движении центра масс. Следствия.
10. Меры движения: количество движения м.т. и механической системы, кинетический момент м.т. и механической системы относительно центра и оси, кинетическая энергия м.т. и мех. системы.
11. Меры действия сил: элементарный импульс силы
12. Кинетическая энергия
13. Теорема об изменении количества движения механической системы в диф. И интегральной форме. Следствия.
14. Момент инерции относительно оси. Радиус инерции. Формулы.
15. Теорема об изменении кинетического момента мех.системы в векторной, скалярной форме. Следствия
16. Диффуры поступательного, вращательного и плоского движения.
17. Теорема об изменении кинетической энергии в диф. И интегральной форме.
18. Теорема Штейнера-Гюйгенса
19. Сила инерции. Принцип Даламбера для м.т.
20. Приведение системы сил инерции к простейшему виду при поступательном, вращательном и плоском движении.
21. Классификация связей: голономные, стационарные и удерживающие. Виртуальное перемещение точки. Виртуальная работа. Идеальная связь.
22. Принцип виртуальных перемещений.
23. Общее уравнение динамики.
24. Обобщенные координаты и скорости. Число степеней свободы.
25. Обобщенные силы и способы вычисления.
26. Условия равновесия механической системы в обобщенных координатах.
27. Уравнение Лагранжа второго рода.

СТАТИКА

Аксиомы статики

Аксиома 1. Две силы, действующие на абсолютно твердое тело уравновешива-ются только тогда, когда они равны по величине и направлены по од-ной прямой в противоположные стороны (рис. 1.2).

 

Рис. 1.2 Рис. 1.3

Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изме-нится, если прибавить к ней или отнять от нее уравновешенную сис-тему сил (рис. 1.3).

Следствие из аксиомы 1 и 2. Действие силы на абсолютно твердое тело (АТТ) не изменится, если точку приложения этой силы перенести по ли-нии ее действия. Пусть на тело в точке А действует сила (рис. 1.4). Добавим в точке В, выбранной произвольно на линии действия си-лы , уравновешенную систему сил и равных по абсолютной величине и направленных по линии ее действия. На основании аксиомы 1 силы и будут уравновешены и их можно отбросить (аксиома 2). В результате получим силу = , но приложенную не в точке А, а в точке В. Отсюда следует, что сила, приложенная к АТТ, есть вектор скользящий.

Рис. 1.4 Рис. 1.5 Рис. 1.6

Аксиома 3 Равнодействующая двух сил, приложенных к АТТ в одной точке, равна

их геометрической сумме , т.е. выражается по моду-лю и направлению диагональю

параллелограмма,построенного на этих силах (рис. 1.5).

Аксиома 4 Всякому действию одного тела на другое соответствует равное по величине,

но противоположное по направлению противодействие. Действие и противодействие-это силы,

приложенные к двум раз-личным телам, поэтому они не уравновешиваются (рис. 1.6).

Аксиома 5 Если деформируемое тело под действием системы сил находится в

равновесии, то при отвердевании его равновесие сохраняется.

Под действием сил тело D находится в равновесии. Если трос CB заменить стержнем,

то равновесие не нарушится, равновесие не нарушится и в том случае, если трос BD

за-менить стержнем, если же стержень АВ заменить тросом - равновесие нарушится

(рис. 1.7).

Рис.1.7

 

Связи и их реакции

 

Системы сходящихся сил. Теорема о существовании равнодействующей. Условия равновесия.

Система сил называется сходящейся, если линии действия всех сил системы пересекаются в одной точке.

Пусть система сходящихся сил (F₁, F₂,...,F_n) приложена к твердому телу (рис. 12, a).

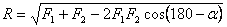
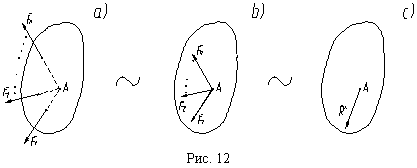Согласно следствию второй аксиомы, переносим все силы системы в точку пересечения линий действия A и получаем систему сил, приложенных в одной точке (рис. 12, b). По аксиоме параллелограмма сил, начиная с сил F₁ и F₂, последовательно складываем силы, добавляя каждый раз к полученной сумме по одной силе системы. Дойдя до последней силы F_n, выясняем, что система сил (рис. 12, b) эквивалентна одной силе или равнодействующей R^* (рис. 12, c), равной геометрической сумме сил системы.

Таким образом, система сходящихся сил приводится к равнодействующей (эквивалентна равнодействующей), которая равна геометрической сумме сил системы и приложена в точке пересечения линий действия сил:

(F1, F2,...,Fn) ~ R^*; R^* = F1 + F2 +... + Fn

Для равновесия твердого тела под действием системы сходящихся сил необходимо и достаточно, чтобы геометрическая сумма всех сил системы была равна нулю:

для равновесия твердого тела под действием системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник системы был замкнутым.