
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическое и аналитическое условие равновесия сходящейся системы сил. Теорема о трех силах.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1.Геометрическое условие равновесия. Так как равнодействующая R сходящихся сил определяется как замыкающаяся сторона силового многоугольника, построенного из этих сил, то Rможет обратиться в нуль тогда и только тогда, когда конец последней силы в многоугольнике совпадает с началом первой, т.е. когда многоугольник замкнётся. Следовательно, для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугльник, постоенный из этих сил, был замкнут. 2.Аналитические условия равновесия. Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трёх координатных осей были равны нулю. Теорема о трёх силах. Если свободное твёрдое тело находится в равновесии под действием трёх непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке. Доказанная теорема выражает необходимое, но недостаточное условие равновесия свободного твёрдого тела под действием трёх сил.
7. Алгебраический момент силы относительно центра и его свойства. Вращательный эффект силы характеризуется ее моментом. Моментом силы F относительно центра О называется величина, равная взятому с соответствующим знаком произведению модуля силы на длину плеча.
8. Понятие о ферме, назначение, применение. Простейшая ферма. Зависимость между количеством шарниров и стержней. Основные определения и допущения. Фермой называется жёсткая конструкция из прямолинейных стержней, соединённых на концах шарнирами. Если все стержни лежат в одной плоскости, ферма называется плоской. Места соединения стержней фермы называют узлами. При расчете фермы трением в узлах и весом стержней (по сравнению с внешними нагрузками) пренебрегают или распределяют веса стержней по узлам. Тогда на каждый из стержней фермы будут действовать две силы, приложенные к его концам, которые при равновесии могут быть направлены только вдоль стержня. Следовательно, можно считать, что стержни фермы работают только на растяжение или на сжатие.
Определения усилий в стержнях фермы методом вырезания узлов. Достоинства и недостатки метода. Этим методом удобно пользоваться, когда надо найти усилия во всех стержнях фермы. Он сводится к последовательному рассмотрению условий равновесия сил, сходящихся в каждом
Как показывают знаки усилий, стержень 5 растянут, остальные сжаты, стержень 7 не нагружен (нулевой стержень). Наличие в ферме нулевых стержней обнаруживается сразу, так как если в узле, не нагруженном внешними силами, сходятся 3 стержзня, из которых 2 направлены вдоль одной прямой, то усилие в третьем стержне равно нулю.
Определения усилий в стержнях фермы методом Риттера. Достоинства и недостатки метода. Этим методом удобно пользоваться для определения усилий в отдельных стержнях фермы, в частности для проверочных расчётов. Идея метода состоит в том, что ферму разделяют на 2 части сечением, проходящих через 3 стержня, в которых требуется определить усилие, и рассматривают равновесие одной из этих частей. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, то есть считая стержни растянутыми. Затем составляют уравнения равновесия или, беря центры моментов так, чтобы в каждое уравнение вошло только одно неизвестное усилие.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1775; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.223.91 (0.011 с.) |

 . Отметим следующие свойства момента силы: 1.Момент силы не изменяется при переносе точкиприложения силы вдоль её линии действия. 2.Момент силы относительно центра О равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через центр О (плечо равно нулю). 3. Момент силы численно выражается удвоенной площадью треугольника ОАВ.
. Отметим следующие свойства момента силы: 1.Момент силы не изменяется при переносе точкиприложения силы вдоль её линии действия. 2.Момент силы относительно центра О равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через центр О (плечо равно нулю). 3. Момент силы численно выражается удвоенной площадью треугольника ОАВ. из узлов фермы. Ход расчётов поясним на конкретном примере. Рассмотрим изображённую на рис,83 ферму, образованную из одинаковых равнобедренных прямоугольных треугольников, действующих на силы параллельны оси x и равны: F1=F2=F3=F=2T. В этой ферме число узлов n=6, а число стержней k=9. Следовательно соотношение выполняется и ферма является жёсткой, без лишних стержней. Составляя уравнения равновесия для фермы в целом, найдём, что реакции опор направлены, как показано на рисунке, и численно равны
из узлов фермы. Ход расчётов поясним на конкретном примере. Рассмотрим изображённую на рис,83 ферму, образованную из одинаковых равнобедренных прямоугольных треугольников, действующих на силы параллельны оси x и равны: F1=F2=F3=F=2T. В этой ферме число узлов n=6, а число стержней k=9. Следовательно соотношение выполняется и ферма является жёсткой, без лишних стержней. Составляя уравнения равновесия для фермы в целом, найдём, что реакции опор направлены, как показано на рисунке, и численно равны  Переходим к определению усилий в стержнях. Пронумеруем узлы фермы римскими цифрами, а стержни арабскими. Искомые усилия будем обозначать
Переходим к определению усилий в стержнях. Пронумеруем узлы фермы римскими цифрами, а стержни арабскими. Искомые усилия будем обозначать  (в стержне 1)…Отрежем мысленно все узлы вместе со сходящимися в нихстержнями от осталтьной фермы. Действие отброшенных частей стержней заменим силами, которые будут направлены вдоль соответствующих стержней и численно равны искомым усилиям
(в стержне 1)…Отрежем мысленно все узлы вместе со сходящимися в нихстержнями от осталтьной фермы. Действие отброшенных частей стержней заменим силами, которые будут направлены вдоль соответствующих стержней и численно равны искомым усилиям  … Изображаем сразу эти силы на рисунке, напрвляя их от узлов, т.е. считая все стержни растянутыми. Теперь для сил, сходящихся в каждом узле, составляем последовательно уравнения равновесия
… Изображаем сразу эти силы на рисунке, напрвляя их от узлов, т.е. считая все стержни растянутыми. Теперь для сил, сходящихся в каждом узле, составляем последовательно уравнения равновесия 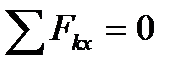 ,
,  . Начинаем с узла 1, где сходятся 2 стержня, так как из 2 уравнений равновесия можно определить только 2 неизвестных усилия. Составляя уравнения равновесия для узла 1, получим
. Начинаем с узла 1, где сходятся 2 стержня, так как из 2 уравнений равновесия можно определить только 2 неизвестных усилия. Составляя уравнения равновесия для узла 1, получим  ,
, 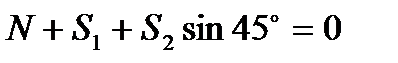 . Отсюда находим
. Отсюда находим  ,
,  Теперь,зная S1, переходим к узлу 2. Для него уравнения равновесия дают S3+F2=0, S4-S1=0,откуда S3=-F=-2T, S4=S1=-1T. Определив S4, составляем аналогичным путём уравнения раывновесия сначала узла 33, а затем узла 4. Из этих уравнений находим:
Теперь,зная S1, переходим к узлу 2. Для него уравнения равновесия дают S3+F2=0, S4-S1=0,откуда S3=-F=-2T, S4=S1=-1T. Определив S4, составляем аналогичным путём уравнения раывновесия сначала узла 33, а затем узла 4. Из этих уравнений находим:  ,
, 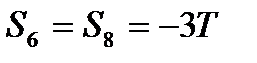 ,
,  . Для вычисления S9 составляем уравнени равновесия сил, сходящихся в узле V, проектируя их на ось By. Получим
. Для вычисления S9 составляем уравнени равновесия сил, сходящихся в узле V, проектируя их на ось By. Получим  , откуда
, откуда  . Второе уравнение равновесия для узла 5 и два уравнения для узла 4 можно составить как поверочные. Для нахождения усилий в стержнях эти уравнения не понадобились, так как вместо них были использованы три уранения равновесия всей фермы в целом при определении
. Второе уравнение равновесия для узла 5 и два уравнения для узла 4 можно составить как поверочные. Для нахождения усилий в стержнях эти уравнения не понадобились, так как вместо них были использованы три уранения равновесия всей фермы в целом при определении  . Окончательные результаты можно занести в таблицу:
. Окончательные результаты можно занести в таблицу:


