
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Центр тяжести и его координаты. Центр тяжести объема, площади, линии. С. 131-132.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Центром тяжести твёрдого тела называется неизменно связанная с этим телом точка, через которую проходит линия действия равнодействующей сил тяжести частиц данного тела при любом положении тела в пространстве. Координаты центра тяжести, как центра параллельных сил, определяются формулами и будут: По таким же формулам можно вычислять координаты центра тяжести тела, если с ним сама система координат непосредственно не связана. Представим себе некоторый объем V, заполненный однородным веществом, имеющим удельный вес γ. Силы тяжести такого тела и некоторой его частицы пропорциональны их объемамЕсливформулы(1)подставитьзначенияРиРk,тополучаем: Выражения (3) определяют положение центра тяжести объема, который является его геометрической характеристикой. Рассмотрим теперь тонкую однородную пластинку весом Р. Эта сила равномерно распределена по всей площади пластинки, так что Р = А γ, где γ – сила тяжести, приходящаяся на единицу площади. Мысленно разобьем всю пластинку на n частей (k = 1, 2,..., n). Очевидно, что сила тяжести Рk равна Аkγ. Выберем систему координат, расположенную в плоскости пластинки,инайдемположениееецентратяжестиС: где xk и yk – координаты центров тяжести выделенной части. Эти формулы определяют положение центра тяжести пластинки, но положение этой точки не зависит ни от силы тяжести, ни от вещества, из которого сделана пластинка. Следовательно, по ним находится положение центра тяжести не самой пластинки, а ее площади. Так мы пришли к понятию«центртяжестиплоскойфигуры»,тоестьгеометрическогообъекта,не обладающего массой. Это понятие является еще одной геометрической характеристикой плоской фигуры. Аналогичными рассуждениями можно прийти к понятию «центр тяжестигеометрическойлинии»: где Lk – длина k-той части, на которые разбита вся линия. В полученных формулах (1.51) – (1.55), определяющих центры тяжести материального и геометрического тел, суммы состоят из бесчисленного множества слагаемых. Правила вычисления таких сумм излагаются в курсе интегрального исчисления.
34. Способы определения координат центра тяжести.с.132 1). Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно или в плоскости симметрии, или на оси симметрии, или в центре симметрии. Допустим, что однородное тело имеет плоскость симметрии. Тогда этой плоскостью оно разбивается н две такие части, веса которых р1 и р2 равны друг другу, а центры тяжести находятся на одинаковых расстояниях от плоскости симметрии. Следовательно, центр тяжести тела как точка, через которую проходит равнодействующая двух равных и параллельных сил р1 и р2, будет действительно лежать в плоскости симметрии. Из свойств симметрии следует, что центр тяжести однородного круглого кольца, круглой или прямоугольной пластины, прямоугольного параллелепипеда, шара и других однородных тел, имеющих центр симметрии, лежит в геометрическом центре этих тел. 2). Разбиение. Если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно, то координаты центра тяжести всего тела можно непосредственно вычислить по формулам
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 567; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.140.232 (0.006 с.) |

 ,
,  ,
,  , где
, где  ,
,  ,
,  - координаты точек приложения сил тяжести
- координаты точек приложения сил тяжести  частиц тела. Согласно определению центр тяжести – это точка геометрическая; она может лежать и вне пределов данного тела. Точку С, координаты которой определяются формулами
частиц тела. Согласно определению центр тяжести – это точка геометрическая; она может лежать и вне пределов данного тела. Точку С, координаты которой определяются формулами  ,
,  ,
,  , называют центром тяжести объёма V. Точку, координаты которой определяются формулами
, называют центром тяжести объёма V. Точку, координаты которой определяются формулами 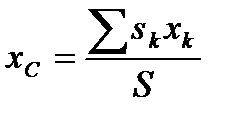
 ,
,  , называют центром тяжести площади S. Координаты центра тяжести линии:
, называют центром тяжести площади S. Координаты центра тяжести линии: 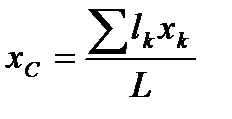 ,
, 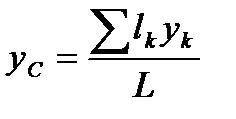 ,
,  . система сил тяжести частиц материального тела имеет свой центр, через который проходит линия действия их равнодействующей. Эта геометрическая точка, принадлежащая телу, называется его центром тяжести. Чтобы найти положение центра тяжести тела, выберем систему координатOxyz,неизменносвязаннуюстелом.ОсьOzнаправимвертикально вверх, то есть параллельно линиям действия сил тяжести. Тогда можно записать:
. система сил тяжести частиц материального тела имеет свой центр, через который проходит линия действия их равнодействующей. Эта геометрическая точка, принадлежащая телу, называется его центром тяжести. Чтобы найти положение центра тяжести тела, выберем систему координатOxyz,неизменносвязаннуюстелом.ОсьOzнаправимвертикально вверх, то есть параллельно линиям действия сил тяжести. Тогда можно записать: ,
,  ,
,  ;
;  ,
,  ,
,  ;
; 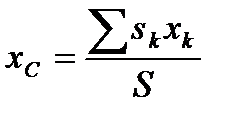 ,
,  ;
;  ,
, 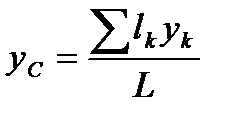 ,
,  . При этом число слагаемых в каждом числителе будет равно числу частей, на которые разбито тело. 3). Дополнение. Этот способ является частным случаем способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. 4). Интегрирование. Если тело нельзя разбить на несколько конечных частей, положения центров тяжести которых известны, то тело разбивают сначала на произвольные малые объёмы
. При этом число слагаемых в каждом числителе будет равно числу частей, на которые разбито тело. 3). Дополнение. Этот способ является частным случаем способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. 4). Интегрирование. Если тело нельзя разбить на несколько конечных частей, положения центров тяжести которых известны, то тело разбивают сначала на произвольные малые объёмы  , для формулы
, для формулы  и т.д., где
и т.д., где  ,
,  ,
,  - координаты некоторой точки, лежащей внутри объёма
- координаты некоторой точки, лежащей внутри объёма 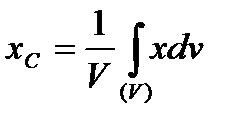 ,
,  ,
,  . Аналогично в других формулах. 5). Экспериментальный способ. Центры тяжести неоднородных тел сложной конфигурации можно определить экспериментально. Один из возможных экспериментальных методов (метод подвешивания) состоит в том, что тело подвешивают на нити или тросе за различные его точки. Направление нити, к которой подвешено тело, будет каждый раз давать направление силы тяжести. Точка пересечения этих направлений определяет центр тяжести тела. Другим возможным способом экспериментального определения центра тяжести является метод взвешивания.
. Аналогично в других формулах. 5). Экспериментальный способ. Центры тяжести неоднородных тел сложной конфигурации можно определить экспериментально. Один из возможных экспериментальных методов (метод подвешивания) состоит в том, что тело подвешивают на нити или тросе за различные его точки. Направление нити, к которой подвешено тело, будет каждый раз давать направление силы тяжести. Точка пересечения этих направлений определяет центр тяжести тела. Другим возможным способом экспериментального определения центра тяжести является метод взвешивания.


