
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способы нахождения мгновенного центра скоростей. С.186-188, с. 203Содержание книги
Поиск на нашем сайте
ЧАСТНЫЕ СЛУЧАИ А) Если плоскопараллельное движение осуществляется путём качения без скольжения одного цилиндрического тела по поверхности другого, причём второе тело неподвижно, то точка касания имеет в данный момент времени скорость, равную нулю, и, следовательно, является мгновенным центром скоростей. Примером служит качение колеса по рельсу. Б) Если скорости точек А и В тела параллельны друг другу, причём линия АВ не перпендикулярна к
Определение ускорений точек при плоскопараллельном движении твердого тела. с.196 Покажем, что ускорение любой точки M тела при плоскопараллельном движении (так же как и скорость) складывается из ускорений, которые она получает в поступательном и во вращательном движениях этого тела. Положение точки M по отношению к осям Oxy определяется радиусом-вектором
Сложное движение точки. Определение понятий относительное, переносное, абсолютное движение. С.212 Совершаемое движение точки (или тела) одновременно по отношению к двум системам отсчёта, из которых одна считается условно неподвижной, а другая определённым образом движется по отношению к первой, называется составным или сложным. Движение, совершаемое точкой M по отношению к подвижным осям координат, называется относительным движением (такое движение будет видеть наблюдатель, связанный с подвижными осями Oxyz и перемещающийся вместе с ними). Движение, совершаемое подвижной системой отсчёта Oxyz и всеми неизменно связанными с ней точками пространства по отношению к неподвижной системе
Теорема об определении скорости точки в сложном движении. С. 215 При сложном движении абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей.
56. Определение ускорения точки в сложном движении (теорема Кориолиса). С. 221
Определения ускорения точки при поступательном переносном движении. С. 219 При поступательном переносном движении абсолютное ускорение точки равно геометрической сумме относительного и переносного ускорений.
|
|||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 319; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.37.200 (0.007 с.) |

 , то мгновенный центр скоростей лежит в бесконечности и скорости всех точек параллельны
, то мгновенный центр скоростей лежит в бесконечности и скорости всех точек параллельны  , т.е.
, т.е.  ; аналогичный результат получается для всех других точек тела. Следовательно, в рассматриваемом случае скорости всех точек тела в данный момент времени равны друг другу и по модулю, и по направлению, т.е. тело имеет мгновенное поступательное распределение скоростей. Угловая скорость тела в этот момент времени равна нулю. В) Если скорости точек А и В тела параллельны друг другу и при этом линия АВ перпендикулярна к
; аналогичный результат получается для всех других точек тела. Следовательно, в рассматриваемом случае скорости всех точек тела в данный момент времени равны друг другу и по модулю, и по направлению, т.е. тело имеет мгновенное поступательное распределение скоростей. Угловая скорость тела в этот момент времени равна нулю. В) Если скорости точек А и В тела параллельны друг другу и при этом линия АВ перпендикулярна к 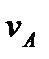 и
и  . Г) Если известен вектор скорости
. Г) Если известен вектор скорости 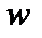 , то положение мгновенного центра скоростей Р, лежащего на перпендикуляре к
, то положение мгновенного центра скоростей Р, лежащего на перпендикуляре к 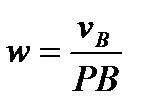 которое даёт
которое даёт 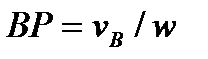 . 1) Вычисляем величину угла
. 1) Вычисляем величину угла  из формулы
из формулы  . 2) От точки А под углом
. 2) От точки А под углом 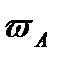 проведём прямую AE, при этом прямая AE должна быть отклонена от
проведём прямую AE, при этом прямая AE должна быть отклонена от  . 3) Откладываем вдоль линии АЕ отрезок AQ, равный
. 3) Откладываем вдоль линии АЕ отрезок AQ, равный 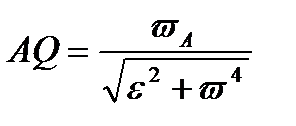 . Построенная таким образом точка Q и будет мгновенным центром ускорений.
. Построенная таким образом точка Q и будет мгновенным центром ускорений. , где
, где 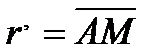 . Тогда
. Тогда 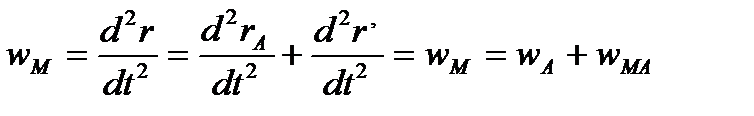 Таким образом, ускорение любой точки M тела геометрически складывается из ускорения какой-нибудь другой точки, принятой за плюс, и ускорения точки M в её вращении вместе с телом вокруг этого аолюса.
Таким образом, ускорение любой точки M тела геометрически складывается из ускорения какой-нибудь другой точки, принятой за плюс, и ускорения точки M в её вращении вместе с телом вокруг этого аолюса. , является для точки M переносным движением. Движение, совершаемое точкой по отношению к неподвижной системе отсчёта
, является для точки M переносным движением. Движение, совершаемое точкой по отношению к неподвижной системе отсчёта 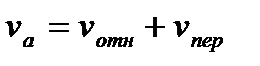 Если угол между напрвлениями векторов
Если угол между напрвлениями векторов  и
и 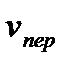 равен
равен 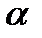 , то по модулю
, то по модулю 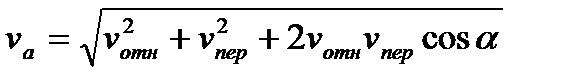
 теорема Кориолиса: абсолютное ускорение точки равно геометрической сумме трёх ускорений: относительного, характеризующего изменение относительной скорости точки в относительном движении, переносного, характеризующего изменение относительной скорости точки в переносном движении и переносной скорости точки в относительном движении.
теорема Кориолиса: абсолютное ускорение точки равно геометрической сумме трёх ускорений: относительного, характеризующего изменение относительной скорости точки в относительном движении, переносного, характеризующего изменение относительной скорости точки в переносном движении и переносной скорости точки в относительном движении.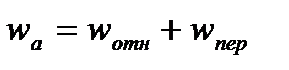 Ускорение любой точки при движении равно геометрической сумме векторов ускорений точки, принятой за полюс, и ускорения во вращательном движении этой точки вместе с плоской фигурой относительно полюса aB = aA + aBA,где а A – ускорение точки, принятой за полюс; aBA – вращательное ускоре ние точки В вокруг А. Вращательноеускорениеточкиопределяетсяпоформуле aBA = aBA + aBA, где ава = ƐАВ – касательное ускорение точки В относительно А.
Ускорение любой точки при движении равно геометрической сумме векторов ускорений точки, принятой за полюс, и ускорения во вращательном движении этой точки вместе с плоской фигурой относительно полюса aB = aA + aBA,где а A – ускорение точки, принятой за полюс; aBA – вращательное ускоре ние точки В вокруг А. Вращательноеускорениеточкиопределяетсяпоформуле aBA = aBA + aBA, где ава = ƐАВ – касательное ускорение точки В относительно А. 


