
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Центр тяжести дуги окружности, треугольника кругового сегмента.с.135Содержание книги
Поиск на нашем сайте
1).Центр тяжести дуги окружности. Рассмотрим дугу AB радиуса R с центральным углом
36. Предмет кинематики. Основные понятия и определения. Задачи кинематики.с.138 Кинематикой называется раздел механики, в котором изучаются геометрические свойства движения тел без учёта их инертности (массы) и действующих на них сил. Под движением мы понимаем в механике изменение с течением времени положения данного тела в пространстве по отношению к другим телам. Для определения положения движущегося тела или точки с тем телом, по отношению к которому изучается движение, жестко связывают какую-нибудь систему координат, которая вместе с телом образуют систему отсчёта. Движение тел совершается в пространстве с течением времени. Пространство в механике мы рассматриваем, как трехмерное евклидово пространство. Все измерения в нём производятся на основании методов евклидовой геометрии. Время является скалярной, непрерывно изменяющейся величиной. Отсчёт времени ведётся от некоторого начального момента, о выборе которого в каждом случае уславливаются. Кинематически задать движение или закон движения тела (точки) значит задать положение этого тела относительно данной системы отсчёта в любой момент времени. Установление математических способов задания движения точек или тел является одной из важных задач кинематики. Основная задача кинематики состоит в том, чтобы, зная закон движения данного тела (или точки), определить все кинематические величины, характеризующие как движение тела в целом, так и движение каждой из его точек в отдельности.
37. Способы задания движения точки. Траектория точки.с.140 Естественный способ задания движения. Непрерывная линия, которую описывает движущаяся точка относительно данной системы отсчёта, называется траекторией точки. Если траекторией является прямая линия, движение точки называется прямолинейным, а если кривая – криволинейным. 1). Естественным способом задания движения удобно пользоваться в тех случаях, когда траектория движущейся точки известна заранее.
38. Определение скорости и ускорения точки при векторном способе задания движения.с.144 Одной из основных кинематических характеристик движения точки является векторная величина, называемая скоростью точки.
39. Определение скорости и ускорения точки при координатном способе задания движения.С.149 1).Определение скорости точки. Вектор скорости точки
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 783; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.34.211 (0.006 с.) |

 . В силу симметрии центр тяжести этой дуги лежит на оси
. В силу симметрии центр тяжести этой дуги лежит на оси 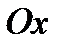 . Найдём координату
. Найдём координату  по формулам
по формулам  ,
,  ,
,  .Для этого выделим на дуге AB элемент
.Для этого выделим на дуге AB элемент  длиною
длиною  , положение которого определяется углом
, положение которого определяется углом  . Координата
. Координата  элемента
элемента  . Подставляя эти значения
. Подставляя эти значения  и
и  в первую из формул и имея в виду, что интеграл должен быть распространён на всю длину дуги, получим:
в первую из формул и имея в виду, что интеграл должен быть распространён на всю длину дуги, получим:  , где L – длина дуги AB, равная
, где L – длина дуги AB, равная  . Отсюда окончательно находим, что центр тяжести дуги окружности лежит на её оси симметрии на расстоянии от центра О, равным
. Отсюда окончательно находим, что центр тяжести дуги окружности лежит на её оси симметрии на расстоянии от центра О, равным  , где угол
, где угол 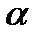 измеряется в радианах. 2). Центр тяжести площади треугольника. Разобьём площадь треугольника ABD прямыми, параллельными стороне AD, на n узких полосок; центры тяжести этих полосок будут, очевидно, лежать в медиане BE треугольника. Следовательно, и центр тяжести всего треугольника лежит на этой медиане. Аналогичный результат получается для двух других медиан. Отсюда заключаем, что центр тяжести площади треугольника лежит в точке пересечения его медиан. При этом известно,
измеряется в радианах. 2). Центр тяжести площади треугольника. Разобьём площадь треугольника ABD прямыми, параллельными стороне AD, на n узких полосок; центры тяжести этих полосок будут, очевидно, лежать в медиане BE треугольника. Следовательно, и центр тяжести всего треугольника лежит на этой медиане. Аналогичный результат получается для двух других медиан. Отсюда заключаем, что центр тяжести площади треугольника лежит в точке пересечения его медиан. При этом известно,  . 3) Центр тяжести площади кругового сектора. Рассмотрим круговой сектор OAB радиуса R с центральным углом
. 3) Центр тяжести площади кругового сектора. Рассмотрим круговой сектор OAB радиуса R с центральным углом  . Разобьём мысленно площадь сектора OAB радиусами, проведёнными из центра О, на n секторов. В пределе, при неограниченном увеличении чиcла n? эти секторы можно рассматривать как плоские треугольники, центры тяжести которых лежат на дуге DE радиуса
. Разобьём мысленно площадь сектора OAB радиусами, проведёнными из центра О, на n секторов. В пределе, при неограниченном увеличении чиcла n? эти секторы можно рассматривать как плоские треугольники, центры тяжести которых лежат на дуге DE радиуса 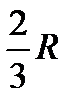 . Следовательно, центр тяжести сектора ОАВ будет совпадать с центром тяжести дуги DE, положение которого найдётся по формуле
. Следовательно, центр тяжести сектора ОАВ будет совпадать с центром тяжести дуги DE, положение которого найдётся по формуле  .
. - уравнение выражает закон движения точки М вдоль траектории. Таким образом, чтобы задать движение точки естественным способом, надо задать: 1) траекторию точки; 2) начало отсчёта на траектории с указанием положительного и отрицательного направлений отсчёта; 3) закон движения точки вдоль траектории в виде
- уравнение выражает закон движения точки М вдоль траектории. Таким образом, чтобы задать движение точки естественным способом, надо задать: 1) траекторию точки; 2) начало отсчёта на траектории с указанием положительного и отрицательного направлений отсчёта; 3) закон движения точки вдоль траектории в виде  . 2) Координатный способ задания движения. Чтобы знать закон движения точки, т.е. ее положение в пространстве в любой момент времени, надо знать значения координат точки для каждого момента времени, т.е. знать зависимости
. 2) Координатный способ задания движения. Чтобы знать закон движения точки, т.е. ее положение в пространстве в любой момент времени, надо знать значения координат точки для каждого момента времени, т.е. знать зависимости  ,
,  ,
,  . Уравнения представляют собой уравнения движения точки в декартовых прямоугольных координатах. Они определяют закон движения точки при координатном способе задания движения. Если движение точки совершается всё время в одной и той же плоскости, то, приняв эту плоскость за плоскость Oxy, мы получим в этом случае два уравнения движения
. Уравнения представляют собой уравнения движения точки в декартовых прямоугольных координатах. Они определяют закон движения точки при координатном способе задания движения. Если движение точки совершается всё время в одной и той же плоскости, то, приняв эту плоскость за плоскость Oxy, мы получим в этом случае два уравнения движения  ,
, 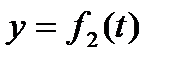 . Уранения представляют собою одновременно уранения траектории точки в параметрической форме, где роль параметра играет время t. Исключив из уравнений движения время, можно найти уравнение траетории в обычной форме, т.е. в виде, дающем зависимость между ее координатами. 3). Векторный способ задания движения.
. Уранения представляют собою одновременно уранения траектории точки в параметрической форме, где роль параметра играет время t. Исключив из уравнений движения время, можно найти уравнение траетории в обычной форме, т.е. в виде, дающем зависимость между ее координатами. 3). Векторный способ задания движения. 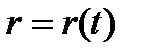 равенство определяет закон криволинейного движения точки в векторной форме, так как оно позволяет в любой момент времени t построить соответствующий вектор к и найти положение движущейся точки. Геометрическое место концов вектора r, т.е. годограф этого вектора, определяет траекторию движущейся точки. Векторный способ задания движения удобен для установления общих зависимостей, так как позволяет описать движение точки одним векторным уравнением вместо трёх скалярных уравнений.
равенство определяет закон криволинейного движения точки в векторной форме, так как оно позволяет в любой момент времени t построить соответствующий вектор к и найти положение движущейся точки. Геометрическое место концов вектора r, т.е. годограф этого вектора, определяет траекторию движущейся точки. Векторный способ задания движения удобен для установления общих зависимостей, так как позволяет описать движение точки одним векторным уравнением вместо трёх скалярных уравнений. . Вектор скорости точки в данный момент времени равен первой производной от радиуса-вектора точки по времени. Формула показывает также, что вектор скорости v равен отношению элементарного перемещения точки dr, направленного по касательной к траектории, к соответствующему промежутку времени dt. При параллельном движении вектор скорости v всё время направлен вдоль прямой, по которой движется точка, и может изменяться лишь по численной величине; при криволинейном движении кроме численной величины всё время изменяется и направление вектора скорости точки. Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки.
. Вектор скорости точки в данный момент времени равен первой производной от радиуса-вектора точки по времени. Формула показывает также, что вектор скорости v равен отношению элементарного перемещения точки dr, направленного по касательной к траектории, к соответствующему промежутку времени dt. При параллельном движении вектор скорости v всё время направлен вдоль прямой, по которой движется точка, и может изменяться лишь по численной величине; при криволинейном движении кроме численной величины всё время изменяется и направление вектора скорости точки. Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки.  - вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиус-вектора точки по времени. Вектор ускорения точки равен отношению элементарного приращения вектора скорости dv к соответствующему промежутку времени dt. В общем случае вектор ускорения лежит в соприкасающейся плоскости и направлен в сторону вогнутости кривой.
- вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиус-вектора точки по времени. Вектор ускорения точки равен отношению элементарного приращения вектора скорости dv к соответствующему промежутку времени dt. В общем случае вектор ускорения лежит в соприкасающейся плоскости и направлен в сторону вогнутости кривой. . Отсюда, учитывая, что
. Отсюда, учитывая, что  ,
, 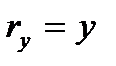 ,
,  , будем иметь:
, будем иметь:  ,
,  ,
,  , или
, или  ,
,  ,
,  , где точка над буквой есть символ дифференцирования по времени. Таким образом, проекции скорости точки на оси координат равны первым производным от соответствующих координат точки по времени
, где точка над буквой есть символ дифференцирования по времени. Таким образом, проекции скорости точки на оси координат равны первым производным от соответствующих координат точки по времени  . 2). Определение ускорения точки. Вектор ускорения точки
. 2). Определение ускорения точки. Вектор ускорения точки 
 . Отсюда на основании теоремы о проекции производной и формул получаем:
. Отсюда на основании теоремы о проекции производной и формул получаем:  ,
,  ,
,  ,
, 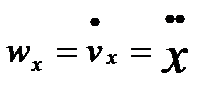 ,
,  ,
,  , т.е. проекции ускорения точки на оси координат равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени
, т.е. проекции ускорения точки на оси координат равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени  .
.


