
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аксиомы статики и следствия из них. Задачи статики.Стр 1 из 7Следующая ⇒
Содержание раздела статика. Основные понятия статики (абсолютно твердое тело, сила, система сил, эквивалентные системы сил, равнодействующая и уравновешивающая сила, взаимоуравновешенная система сил, равновесие). Статикой называется раздел механики, в котором излагается общее учение о силах и изучаются условия равновесия материальных тел, находящихся под действием сил. Абсолютно твёрдое тело – это т акое тело, расстояние между двумя любыми точками которого всегда остаётся постоянным. Сила – величина, являющаяся количественной мерой механического взаимодействия материальных тел. Система сил – совокупность сил, действующих на какое-нибудь твёрдое тело. Если одну систему сил, действующих на свободное твёрдое тело, можно заменить другой системой, не изменяя при этом состояния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными. Равнодействующая – это сила, которая одна заменяет действие данной системы сил на твёрдое тело. Сила, равная равнодействующей по модулю, прямо противоположная ей по направлению и действующая вдоль той же прямой, называется уравновешивающей силой. Система сил, под действием которой свободное твёрдое тело может находится в покое, называется уравновешенной. Равновесие- состояние покоя.
Аксиомы статики и следствия из них. Задачи статики. Аксиома 1. Если на свободное абсолютно твёрдое тело действует две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю и направлены вдоль одной прямой в противоположные стороны. Аксиома 2. Действие данной системы сил на абсолютно твёрдое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил. Следствие из 1-й и 2-й аксиом. Действие силы на абсолютно твёрдое тело не изменится, если перенести точку приложения силы вдоль её линии действия в любую другуюточку тела. Аксиома 3. Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, постоенного на этих силах, как на сторонах. Аксиома 4. При всяком действии одного материального тела на другое имеет место такое же по величине, но противоположное по направлению противодействие. Аксиома 5. Равновесие изменяемого тела, находящегося под действием данной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твёрдым). Аксиома связей. Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями этих связей. Содержание статики абсолютно твердого тела составляют две основные задачи: 1.Задача о приведении системы сил: как данную систему сил заменить другой, наиболее простой, ей эквивалентной? 2.Задача о равновесии: каким условиям должна удовлетворять система сил, приложенная к данному телу (или материальной точке), чтобы она была уравновешенной системой?
Свободное и несвободное твердое тело. Связи и реакции связей. Основные типы связей и их реакции. Аксиома связей. Тело, которое не скреплено с другими телами и может совершить из данного положения любые перемещения в пространстве, называется свободным. Тело, перемещениям которого в пространстве препятствуют какие-нибудь другие, скреплённые или соприкасающиеся с ним тела, называется несвободным. Всё то, что ограничивает перемещения данного тела в пространстве, называется связью. Сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям, называется силой реакции или реакцией связи. 1.Гладкая плоскость или опора. Гладкой будем называть поверхность, трением о которую данного тела можно в первом приближении пренебречь. Реакция N гладкой поверхности или опоры направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена в этой точке. 2.Нить. Реакция Т натянутой нити направлена вдоль нити к точке её подвеса. 3.Цилиндрический шарнир (подшипник). Реакция R цилиндрического шарнира может иметь любое направление в плоскости, перпендикулярной к оси шарнира. 4.Шаровой шарнир и подпятник. Этот вид связи закрепляет какую-либо точку тела так, что она не может совершать никаких перемещений в пространстве. Реакция R шарового шарнира или подпятника может иметь любое направление в пространстве. 5.Стержень. Реакция N стержня направлена вдоль оси стержня. Аксиома связей. Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями этих связей.
Равнодействующая сходящейся системы сил и способы ее нахождения. Система сходящихся сил имеет равнодействующую, равную геометрической сумме (главному вектору) этих сил и приложенную в точке их пересечения. Равнодействующую сходящейся системы сил можно найти сложением системы сил. Геометрическая сумма любой системы сил определяется или последовательным сложением сил системы по правилу параллелограмма, или построением силового многоуголника. При построении силового многоугольника порядок, в котором будут откладываться векторы сил, модуль и направление R не значителен. Проделанное построение представляет собою результат последовательного применения правила силового треугольника.
Определения усилий в стержнях фермы методом вырезания узлов. Достоинства и недостатки метода. Этим методом удобно пользоваться, когда надо найти усилия во всех стержнях фермы. Он сводится к последовательному рассмотрению условий равновесия сил, сходящихся в каждом
Как показывают знаки усилий, стержень 5 растянут, остальные сжаты, стержень 7 не нагружен (нулевой стержень). Наличие в ферме нулевых стержней обнаруживается сразу, так как если в узле, не нагруженном внешними силами, сходятся 3 стержзня, из которых 2 направлены вдоль одной прямой, то усилие в третьем стержне равно нулю.
Определения усилий в стержнях фермы методом Риттера. Достоинства и недостатки метода. Этим методом удобно пользоваться для определения усилий в отдельных стержнях фермы, в частности для проверочных расчётов. Идея метода состоит в том, что ферму разделяют на 2 части сечением, проходящих через 3 стержня, в которых требуется определить усилие, и рассматривают равновесие одной из этих частей. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, то есть считая стержни растянутыми. Затем составляют уравнения равновесия или, беря центры моментов так, чтобы в каждое уравнение вошло только одно неизвестное усилие.
Определения ускорения точки при поступательном переносном движении. С. 219 При поступательном переносном движении абсолютное ускорение точки равно геометрической сумме относительного и переносного ускорений.
Содержание раздела статика. Основные понятия статики (абсолютно твердое тело, сила, система сил, эквивалентные системы сил, равнодействующая и уравновешивающая сила, взаимоуравновешенная система сил, равновесие). Статикой называется раздел механики, в котором излагается общее учение о силах и изучаются условия равновесия материальных тел, находящихся под действием сил. Абсолютно твёрдое тело – это т акое тело, расстояние между двумя любыми точками которого всегда остаётся постоянным. Сила – величина, являющаяся количественной мерой механического взаимодействия материальных тел. Система сил – совокупность сил, действующих на какое-нибудь твёрдое тело. Если одну систему сил, действующих на свободное твёрдое тело, можно заменить другой системой, не изменяя при этом состояния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными. Равнодействующая – это сила, которая одна заменяет действие данной системы сил на твёрдое тело. Сила, равная равнодействующей по модулю, прямо противоположная ей по направлению и действующая вдоль той же прямой, называется уравновешивающей силой. Система сил, под действием которой свободное твёрдое тело может находится в покое, называется уравновешенной. Равновесие- состояние покоя.
Аксиомы статики и следствия из них. Задачи статики. Аксиома 1. Если на свободное абсолютно твёрдое тело действует две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю и направлены вдоль одной прямой в противоположные стороны. Аксиома 2. Действие данной системы сил на абсолютно твёрдое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил. Следствие из 1-й и 2-й аксиом. Действие силы на абсолютно твёрдое тело не изменится, если перенести точку приложения силы вдоль её линии действия в любую другуюточку тела. Аксиома 3. Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, постоенного на этих силах, как на сторонах. Аксиома 4. При всяком действии одного материального тела на другое имеет место такое же по величине, но противоположное по направлению противодействие. Аксиома 5. Равновесие изменяемого тела, находящегося под действием данной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твёрдым). Аксиома связей. Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями этих связей. Содержание статики абсолютно твердого тела составляют две основные задачи: 1.Задача о приведении системы сил: как данную систему сил заменить другой, наиболее простой, ей эквивалентной? 2.Задача о равновесии: каким условиям должна удовлетворять система сил, приложенная к данному телу (или материальной точке), чтобы она была уравновешенной системой?
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 874; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.152.251 (0.016 с.) |
 из узлов фермы. Ход расчётов поясним на конкретном примере. Рассмотрим изображённую на рис,83 ферму, образованную из одинаковых равнобедренных прямоугольных треугольников, действующих на силы параллельны оси x и равны: F1=F2=F3=F=2T. В этой ферме число узлов n=6, а число стержней k=9. Следовательно соотношение выполняется и ферма является жёсткой, без лишних стержней. Составляя уравнения равновесия для фермы в целом, найдём, что реакции опор направлены, как показано на рисунке, и численно равны
из узлов фермы. Ход расчётов поясним на конкретном примере. Рассмотрим изображённую на рис,83 ферму, образованную из одинаковых равнобедренных прямоугольных треугольников, действующих на силы параллельны оси x и равны: F1=F2=F3=F=2T. В этой ферме число узлов n=6, а число стержней k=9. Следовательно соотношение выполняется и ферма является жёсткой, без лишних стержней. Составляя уравнения равновесия для фермы в целом, найдём, что реакции опор направлены, как показано на рисунке, и численно равны  Переходим к определению усилий в стержнях. Пронумеруем узлы фермы римскими цифрами, а стержни арабскими. Искомые усилия будем обозначать
Переходим к определению усилий в стержнях. Пронумеруем узлы фермы римскими цифрами, а стержни арабскими. Искомые усилия будем обозначать  (в стержне 1)…Отрежем мысленно все узлы вместе со сходящимися в нихстержнями от осталтьной фермы. Действие отброшенных частей стержней заменим силами, которые будут направлены вдоль соответствующих стержней и численно равны искомым усилиям
(в стержне 1)…Отрежем мысленно все узлы вместе со сходящимися в нихстержнями от осталтьной фермы. Действие отброшенных частей стержней заменим силами, которые будут направлены вдоль соответствующих стержней и численно равны искомым усилиям  … Изображаем сразу эти силы на рисунке, напрвляя их от узлов, т.е. считая все стержни растянутыми. Теперь для сил, сходящихся в каждом узле, составляем последовательно уравнения равновесия
… Изображаем сразу эти силы на рисунке, напрвляя их от узлов, т.е. считая все стержни растянутыми. Теперь для сил, сходящихся в каждом узле, составляем последовательно уравнения равновесия 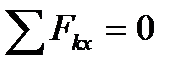 ,
,  . Начинаем с узла 1, где сходятся 2 стержня, так как из 2 уравнений равновесия можно определить только 2 неизвестных усилия. Составляя уравнения равновесия для узла 1, получим
. Начинаем с узла 1, где сходятся 2 стержня, так как из 2 уравнений равновесия можно определить только 2 неизвестных усилия. Составляя уравнения равновесия для узла 1, получим  ,
, 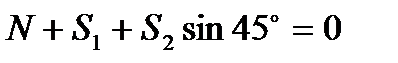 . Отсюда находим
. Отсюда находим  ,
,  Теперь,зная S1, переходим к узлу 2. Для него уравнения равновесия дают S3+F2=0, S4-S1=0,откуда S3=-F=-2T, S4=S1=-1T. Определив S4, составляем аналогичным путём уравнения раывновесия сначала узла 33, а затем узла 4. Из этих уравнений находим:
Теперь,зная S1, переходим к узлу 2. Для него уравнения равновесия дают S3+F2=0, S4-S1=0,откуда S3=-F=-2T, S4=S1=-1T. Определив S4, составляем аналогичным путём уравнения раывновесия сначала узла 33, а затем узла 4. Из этих уравнений находим:  ,
, 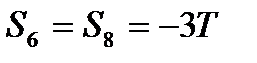 ,
,  . Для вычисления S9 составляем уравнени равновесия сил, сходящихся в узле V, проектируя их на ось By. Получим
. Для вычисления S9 составляем уравнени равновесия сил, сходящихся в узле V, проектируя их на ось By. Получим  , откуда
, откуда  . Второе уравнение равновесия для узла 5 и два уравнения для узла 4 можно составить как поверочные. Для нахождения усилий в стержнях эти уравнения не понадобились, так как вместо них были использованы три уранения равновесия всей фермы в целом при определении
. Второе уравнение равновесия для узла 5 и два уравнения для узла 4 можно составить как поверочные. Для нахождения усилий в стержнях эти уравнения не понадобились, так как вместо них были использованы три уранения равновесия всей фермы в целом при определении  . Окончательные результаты можно занести в таблицу:
. Окончательные результаты можно занести в таблицу: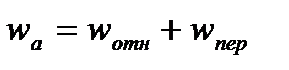 Ускорение любой точки при движении равно геометрической сумме векторов ускорений точки, принятой за полюс, и ускорения во вращательном движении этой точки вместе с плоской фигурой относительно полюса aB = aA + aBA,где а A – ускорение точки, принятой за полюс; aBA – вращательное ускоре ние точки В вокруг А. Вращательноеускорениеточкиопределяетсяпоформуле aBA = aBA + aBA, где ава = ƐАВ – касательное ускорение точки В относительно А.
Ускорение любой точки при движении равно геометрической сумме векторов ускорений точки, принятой за полюс, и ускорения во вращательном движении этой точки вместе с плоской фигурой относительно полюса aB = aA + aBA,где а A – ускорение точки, принятой за полюс; aBA – вращательное ускоре ние точки В вокруг А. Вращательноеускорениеточкиопределяетсяпоформуле aBA = aBA + aBA, где ава = ƐАВ – касательное ускорение точки В относительно А. 


