Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение главных центральных моментов инерции сеченияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 1. Определяют положение центра тяжести сечения (см. порядок решения задачи для практической работы № 4). 2. Проводят центральные оси для каждого профиля проката или простой геометрической фигуры. Эти оси называются центральными осями. 3. Проводят главные центральные оси. Они проходят через центр тяжести всего сечения. Одну из осей совмещают с осью симметрии, а вторую проводят через центр тяжести сечения перпендикулярно первой. Вертикальная ось обозначается v, а горизонтальная – u. 4. Находят моменты инерции сечения относительно главных центральных осей. В общем виде моменты инерции сечения определяют по формулам: относительно оси и
относительно оси v
где Ju и Jv – моментыинерции сечения относительно главных центральных осей u и v; Моменты инерции простых фигур относительно осей u и v определяются по формулам: относительно оси и
относительно оси v
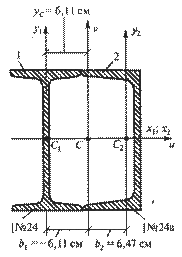
где Если главная центральная ось совпадает с собственной центральной осью какого-нибудь профиля или фигуры, то момент инерции ее относительно главной центральной оси равен моменту инерции относительно собственной оси, т.к. расстояние между ними равно нулю. Пример 9. Определить момент инерции сечения, показанного на рис. 15, относительно главной центральной оси, не являющейся осью симметрии сечения. Сечение состоит из двутавра № 24 и швеллера № 24а. Решение. 1. Определяют положение центра тяжести сечения (см. пример 4). Центр тяжести сечения xC= 6,11 см; yC=0. 2. Проведем центральные оси х1, х2 и y1, y2. Оси x1 и х2 совпали. 3. Проведем главные центральные оси. Ось и совмещаем с осью симметрии, а ось v проводим через центра тяжести С перпендикулярно оси и. Оси и, х1 и х2 совпали. 4. Определим момент инерции сечения относительно оси v, т.к. по условию требуется найти момент инерции только относительно оси, не являющейся осью симметрии. Запишем формулу:
Рис. 15 В этой формуле
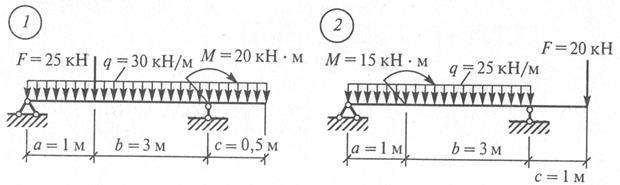
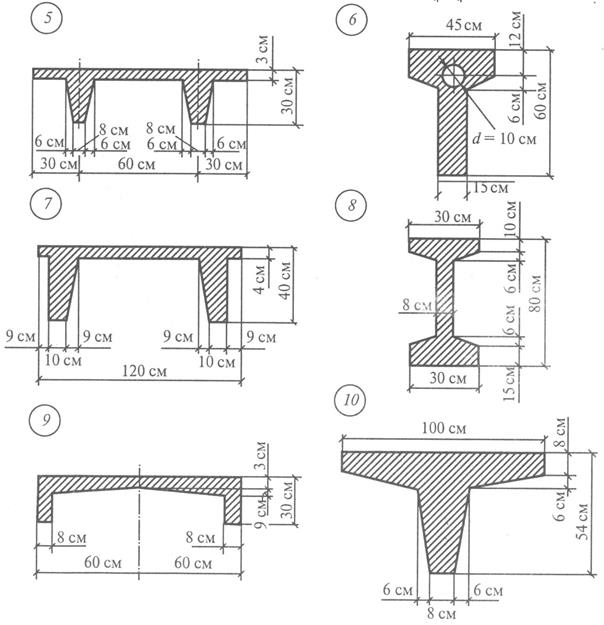
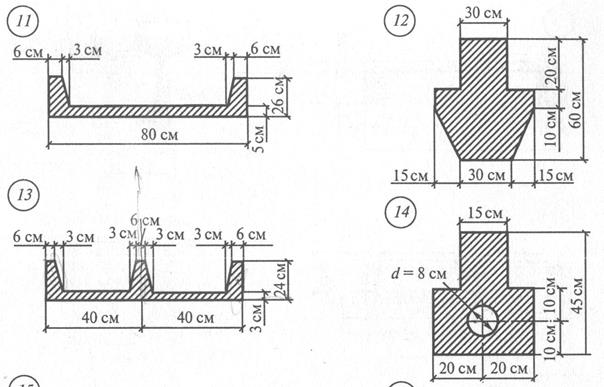
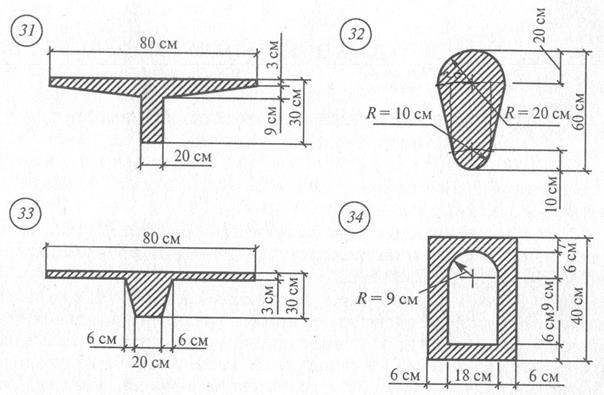
где Тогда Jv= 1497+1631=3128 см4. Ответ: Jv= 3128 см4. Задание для практической работы № 8. Определить момент инерции сечения относительно главной центральной оси, не являющейся осью симметрии, по данным одного из вариантов, показанных на рис. 16.
Рис. 16
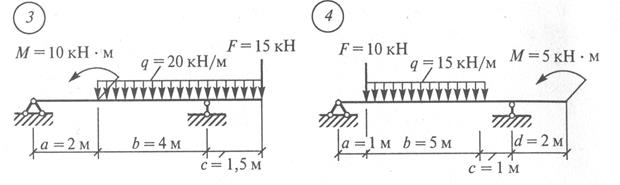
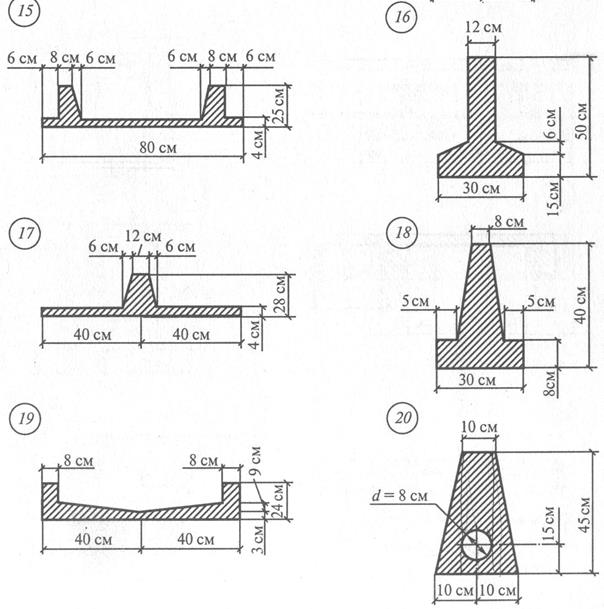
Рис. 16 Продолжение
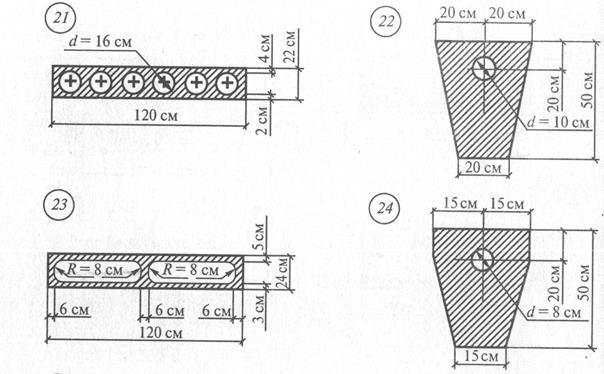
Рис. 16 Продолжение
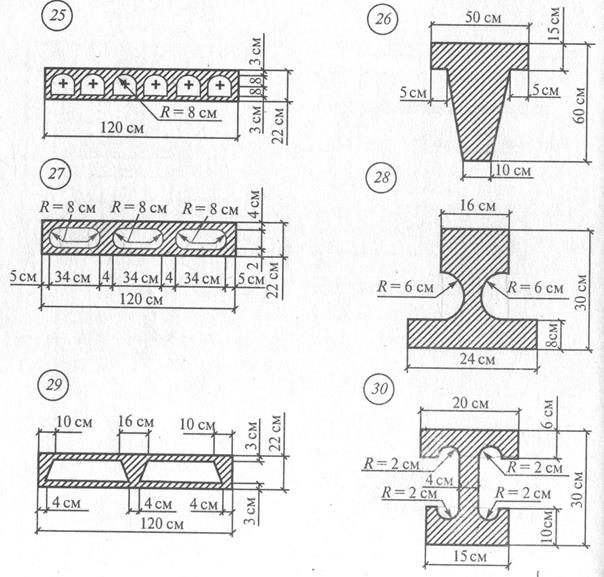
Рис. 16 Продолжение
Рис. 16 Окончание
Практическая работа № 9 Построение эпюр поперечных сил и изгибающих Моментов для простой балки 1. Определяют реакции балки (см. порядок решения в практической работе № 2). 2. Обозначают характерные сечения (точки) балки. Ими являются концевые сечения балки, опоры, точки приложения сосредоточенных сил и моментов, начало и конец распределенной нагрузки. 3. Строят эпюру поперечных сил Qх. Для этого определяют значения поперечных сил а характерных точках. Поперечная сила в сечении равна сумме проекций всех сил, расположенных слева (справа) от рассматриваемого сечения, на ось, перпендикулярную оси элемента. Силу, расположенную слева от рассматриваемого сечения и направленную вверх, считаю положительной, а направленную вниз – отрицательной. Для правой части балки – наоборот. В сечениях, соответствующих точкам приложения сосредоточенных сил, в том числе в точках приложения опорных реакций, необходимо определить два значения поперечной силы: чуть левее и чуть правее рассматриваемой точки. Поперечные силы в этих сечениях обозначаются соответственно Qлев и Qправ. Найденныезначения поперечных сил в характерных точках откладываются в некотором масштабе от нулевой линии. Эти значения соединяются прямыми линиями по следующим правила: а) если к участку балки нет распределенной нагрузки, то под этим участком значения поперечных сил соединяются прямой линией, параллельной нулевой линии; б) если на участке балки приложена распределенная нагрузка, то под этим участком значения поперечных сил соединяются прямой, наклонной к нулевой линии. Она может пересекать или не пересекать нулевую линию. Соединив все значения поперечных сил по указанным правилам, получим график изменения поперечных сил по длине балки. Такой график называется эпюрой Qx. 4. Строят эпюру изгибающих моментов Мх. Для этого определяют изгибающие моменты в характерных точках. Изгибающий момент в рассматриваемом сечении равен сумме моментов всех сил, расположенных слева (справа) от этого сечения. В сечениях, соответствующих точкам приложения сосредоточенных моментов, не6обходимо определить два значения изгибающего момента – чуть левее и чуть правее рассматриваемой точки. Изгибающие моменты в этих точках обозначаются соответственно Млев и Мправ. Полученные значения откладываются в некотором масштабе от нулевой линии. эти значения соединяются в соответствии со следующими правилами: а) если на участке балки нет распределенной нагрузки, то под этим участком балки два соседних значения изгибающих моментов соединяются прямой линией; б) если к участку балки приложена распределенная нагрузка, то под этим участком значения изгибающих моментов соединяются по параболе. Парабола имеет выпуклость в сторону действия нагрузки. При этом, если эпюра Qx на рассматриваемом участке не пересекает нулевую линию, то эпюру Мх (она является параболой) может быть построена по двум точкам, т.к. все значения изгибающих моментов в промежуточных точках находятся между значениями в характерных точках. Если эпюра Qx пересекает нулевую линию, то под этим участком эпюра Мх будет иметь экстремальное (максимальное или минимальное) значение или вершину параболы. Положение этой точки находится по эпюре из подобия треугольников. Затем находят значение изгибающего момента в этой точке и строят эпюру на участке распределенной нагрузки по трем точкам. Соединив все значения изгибающих моментов по указанным правилам, получим график изменения изгибающих моментов по длине балки. Такой график называется эпюрой Мx. Существует несколько способов проверки правильности построения эпюр. Наиболе6е простой способ проверки заключается в том, что суммы моментов всех левых и всех правых сил, взятые отдельно, в любой точке балки должны быть равны между собой.
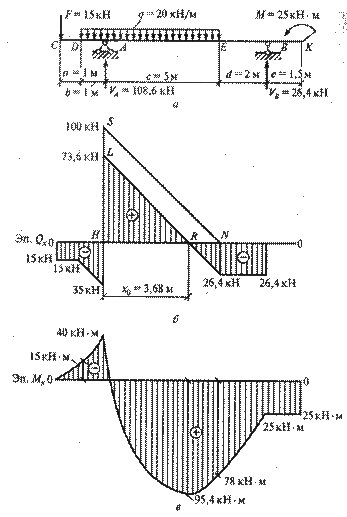
Пример 10. Построить эпюры Qx и Мx балки, показанной на рис. 17, а. Решение. 1. Определим опорные реакции балки. Составим уравнения: 1) Из первого уравнения найдем VB:
или
откуда Из второго уравнения найдем VА:
или откуда Выполним проверку:
или
Рис. 17
2. Обозначим характерные сечения балки C, D, A, E, B. K. 3. Строим эпюру Qx. Определим значения поперечных сил в характерных сечениях:
Соединим полученные значения прямыми линиями (рис. 17, б) и получим эпюру Qx. Эпюра Qx на участке АЕ пересекает нулевую линию. Определим положение точки, в которой эпюра Qx пересекает нулевую линию. Рассмотрим подобие треугольников HRL и HNS (см. рис. 17, б), откуда HR/HN = HL/HS, или x0/5 = 73,6/100, откуда
Это сечение считается также характерным для эпюры Qx и Мx. 4. Строим эпюру Мx (см. рис. 17, в). Определим изгибающие моменты в характерных точках:
5. Проверка. В качестве проверки возьмем сумму моментов всех сил относительно точки, расположенной на расстоянии x0 от левой опоры, но рассмотрим правую часть балки:
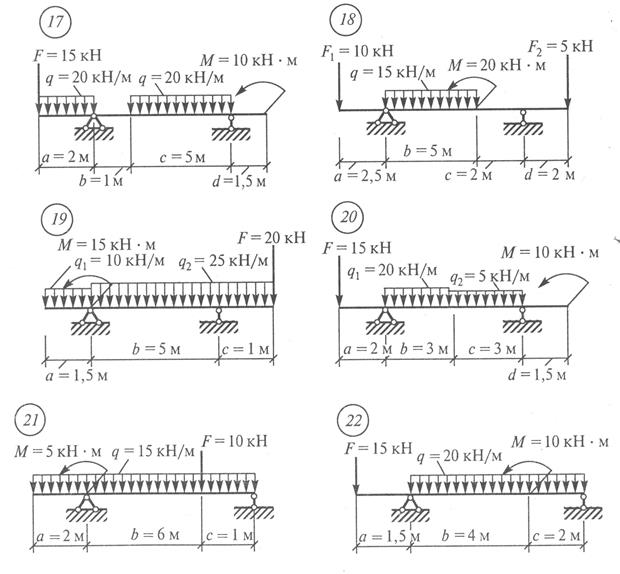
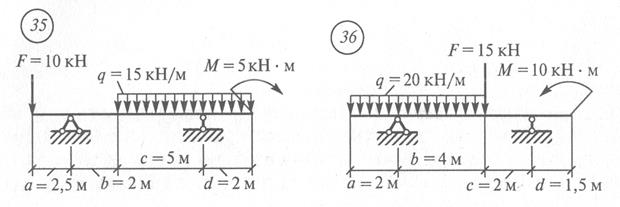
Разница в значениях Мx при рассмотрении левых и правых сил возможна из-за округления величин опорных реакций и расстояния x0. Задание для практической работы № 9. Построить эпюры Qx и Мx балки по данным одного из вариантов, показанных на рис. 18.
РРРHhhiuHис. 18
Рис. 18 Продолжение
Рис. 18 Продолжение
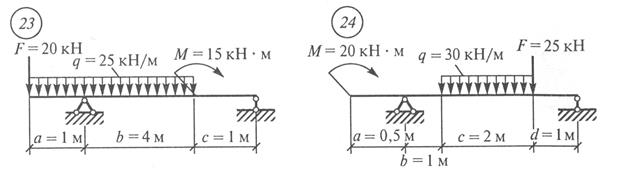
Рис. 18 Окончание
Практическая работа № 10
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 7768; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

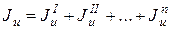 ;
; ,
,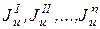 - моменты инерции простых фигур относительно главной центральной оси u;
- моменты инерции простых фигур относительно главной центральной оси u; 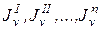 - моменты инерции простых фигур относительно главной центральной оси v.
- моменты инерции простых фигур относительно главной центральной оси v.
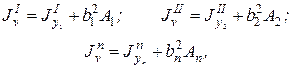
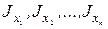 - моменты инерции простых фигур относительно собственных центральных осей x1, x2, …, xn. Они определяются по таблицам ГОСТов (см. прил. I) для профилей прокатной стали и формулам для простых геометрических фигур (см. прил. II).
- моменты инерции простых фигур относительно собственных центральных осей x1, x2, …, xn. Они определяются по таблицам ГОСТов (см. прил. I) для профилей прокатной стали и формулам для простых геометрических фигур (см. прил. II).  - моменты инерции простых фигур относительно собственных центральных осей y1, y2, …, yn; а1, а2, …, аn – расстояние от главной центральной оси и до центральных осей x1, x2, …, xn; b1, b2, …, bn – расстояние от главной центральной оси v до центральных осей y1, y2, …, yn; А1, А2, …, Аn – площади сечений профилей прокатной стали или простых геометрических фигур.
- моменты инерции простых фигур относительно собственных центральных осей y1, y2, …, yn; а1, а2, …, аn – расстояние от главной центральной оси и до центральных осей x1, x2, …, xn; b1, b2, …, bn – расстояние от главной центральной оси v до центральных осей y1, y2, …, yn; А1, А2, …, Аn – площади сечений профилей прокатной стали или простых геометрических фигур.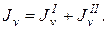
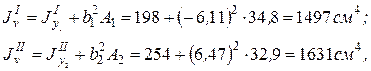
 (см. табл. 3, прил. I);
(см. табл. 3, прил. I);  (см. табл. 4, прил. I); b1= - 6,11 см;
(см. табл. 4, прил. I); b1= - 6,11 см;  (см. рис. 14 и табл. 3 и 4, прил. I).
(см. рис. 14 и табл. 3 и 4, прил. I).

 2)
2) 

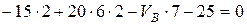 ,
,
 .
.
 ,
, .
.
 откуда
откуда  .
.