
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 1. Теоретическая механикаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
I. Пояснительная записка
Учебной дисциплиной «Техническая механика» предусматривается изучение общих законов движения и равновесия, материальных тел, основ расчета элементов конструкций на прочность, жесткость и устойчивость, а также статического расчета сооружений. Материал, выносимый на установочные и обзорные занятия, а также перечень выполняемых лабораторных работ и практических занятий определен учебным заведением исходя из профиля подготовки выпускника, контингента студентов и соответствующих учебных планов, согласованных с Управлением кадров и учебных заведений Госстроя России. На установочных занятиях студентов знакомят с программой дисциплины, методикой работы над учебным материалом и дают разъяснения по выполнению двух домашних контрольных работ. Обзорные лекции проводятся по сложным для самостоятельного изучения темам программы. Проведение практических занятий предусматривает своей целью закрепление теоретических знаний и приобретение практических умений по программе учебной дисциплины. Выполнение домашних контрольных работ определяет степень усвоения студентами изученного материала и умение применять полученные знания при решении практических задач. Учебный материал рекомендуется изучать в той последовательности, которая дана в методических указаниях: - ознакомление с примерным тематическим планом и методическими указаниями по темам; - изучение программного материала по рекомендуемой литературе; - составление ответов на вопросы для самоконтроля, приведенные после каждой темы. В результате изучения дисциплины студент должен: иметь представление: - об общих законах движения и равновесия материальных тел; - о видах деформаций и основных расчетах на прочность, жесткость и устойчивость элементов сооружений; знать: - основные понятия, законы и методы механики деформируемого твердого тела; уметь: - выполнять расчеты на прочность, жесткость и устойчивость элементов сооружений; - пользоваться государственными стандартами, строительными нормами и правилами и другой нормативной документацией.
II. Примерный тематический план
III. Литература
1. Бычков Д.В. Теоретическая механика. Учебник для техникумов. Изд. 4-е, испр. – М.: «Высшая школа», 1976. – 240 с. 2. Ивченко В.А. Техническая механика: Учебное пособие. – М.: ИНФРА-М, 2003. – 157 с. 3. Сетков В.И. Сборник задач по технической механике: Учебное пособие для среднего профессионального образования. – М.: Издательский дом «Академия», 2003. – 224 с. 4. Эрдеди А.А. Теоретическая механика. Сопротивление материалов: Учебное пособие. 4-е изд., перераб. и доп. – М.: «Высшая школа», 2002. – 318 с. IV. Методические указания по темам и вопросы для самоконтроля
Введение Следует уяснить содержание дисциплины, основные понятия: материальное тело, механическое движение, равновесие. Вопросы для самоконтроля: 1. Что изучает техническая механика? 2. Что такое материя? 3. Что такое движение материи, какие формы движения вы знаете, что такое механическое движение? 4. что изучается в теоретической механике и ее разделах: статике, кинематике, динамике?
Раздел 1. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статикаявляется частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил. Успешное овладение методиками статики – необходимое условие для изучения всех последующих тем и разделов дисциплины техничкой механики.
Тема 1.1 Основные понятия и аксиомы статики
Следует глубоко вникнуть в физический смысл аксиом статики. Изучая связи и их реакции, нужно иметь в виду, что реакция связи является силой противодействия и направлена всегда противоположно силе действия рассматриваемого тела на связь (опору). Вопросы для самоконтроля: 1. Какое тело называется абсолютно твердым? 2. Что называется материальной точкой? 3. Что такое сила и какова ее единица? Какими тремя факторами определяется сила, действующая на твердое тело? 4. Что называется системой сил? 5. Какие две системы называются эквивалентными? 6. Какая сила называется равнодействующей данной системе сил? 7. Чем отличается равнодействующая данной системы сил от силы, уравновешивающей эту систему? 8. Что такое аксиомы статики, как они формулируются? 9. Какое тело называется несвободным? 10. Что называется реакцией связи, как направлены реакции наиболее распространенных типов связей? Тема 1.2 Плоская система сходящихся сил
При изучении темы следует иметь ввиду, что эта система эквивалента одной силе (равнодействующей) и стремится придать телу (в случае, если точка схождения сил совпадает с центром тяжести тела) прямолинейное движение. Равновесие тела будет иметь место в случае равенства равнодействующей нулю. Геометрическим условием равновесия является замкнутость многоугольника, построенного на силах системы, аналитическим условием – равенство нулю алгебраических сумм проекций сил системы на любые две взаимно перпендикулярные оси. Следует получить навыки в решении задач на равновесие тел, обратив особое внимание на рациональный выбор направления координатных осей. Вопросы для самоконтроля: 1. Какие силы называются сходящимися? 2. По какой формуле определяется величина равнодействующей двух сходящихся сил? 3. Как геометрически определяется равнодействующая системы сходящихся сил, влияет ли порядок сложения сил на величину и направление сходящихся сил? 4. В чем состоит геометрическое условие равновесия системы сходящихся сил? 5. Сформулируйте теорему о равновесии трех непараллельных сил. 6. Что называется проекцией силы на ось, как определяется знак проекции? 7. Известно, что сумма проекций всех сил, приложенных к телу на одну из двух взаимно перпендикулярных осей, равна нулю, на другую – не равна нулю. Как направлена равнодействующая такой системы сил? Чему равна проекция этой равнодействующей на другую ось? 8. Как формулируются аналитические условия равновесия системы сходящихся сил? 9. В чем заключается сущность определения сил в стержнях ферм методом вырезания узлов? Тема 1.3 Пара сил При изучении темы следует знать, что система пар сил эквивалентна одной паре (равнодействующей) и стремится придать телу вращательное движение. Равновесие тела будет иметь место в случае равенства нулю момента равнодействующей пары. Аналитическим условием равновесия является равенство нулю алгебраической суммы моментов пар системы. Следует обратить внимание на определение момента силы относительно точки. Необходимо помнить, что момент силы относительно точки равен нулю лишь в том случае, если точка лежит на линии действия силы. Вопросы для самоконтроля: 1. Что называется парой сил? 2. Какое движение совершает свободное тело под действием пары сил? 3. Что называется моментом пары и как определяется знак момента? Какова единица момента? 4. Каким образом можно уравновесить действие на тело пары сил? 5. Какие пары сил называются эквивалентными? 6. Какими свойствами обладают пары сил? 7. В чем состоит условие равновесия пар, лежащих в одной плоскости?
Вопросы для самоконтроля. 1. Какое равновесие твердого тела называется устойчивым, неустойчивым и безразличным? 2. При каком условии равновесие твердого тела, имеющего точку опоры или ось вращения, устойчивое, при каком – неустойчивое и при каком – безразличное? Приведите примеры. 3. Сформулируйте условие равновесия для тела, опирающегося на плоскость. 4. Что такое коэффициент устойчивости тела, имеющего плоскость опоры? Каким он должен быть – больше или меньше единицы?
Тема 2.1 Основные положения
При изучении темы следует усвоить, что внутренние силы, возникающие между частицами тела под действием нагрузок, являются таковыми для тела в целом; при применении метода сечений эти силы для рассматриваемой части тела являются внешними, т.е. к ним применимы методы статики. Действующая в проведенном поперченном сечении система внутренних сил эквивалентна в общем случае одной силе и одному моменту. Разложив их на составляющие, получим соответственно три силы (по направлению координатных осей) и три момента (относительно этих осей), которые называют внутренними силовыми факторами (ВСФ). Возникновение тех или иных ВСФ зависит от фактического нагружения бруса. Определяют ВСФ с помощью уравнений равновесия статики. Внутренним нормальным силам соответствуют нормальные напряжения δ, касательным силам – касательные напряжения τ. Вопросы для самоконтроля: 1. Каковы основные задачи науки о сопротивлении материалов? 2. Что называется прочностью, жесткостью и устойчивостью элемента конструкции? 3. Какие деформации называются упругими и какие пластическими (остаточными)? 4. Что называется упругостью твердого тела? 5. Как классифицируются нагрузки, действующие на сооружения? 6. Сформулируйте основные гипотезы и допущения, принимаемые в сопротивлении материалов. 7. Что такое брус, пластинка (оболочка) и массивное тело? 8. В чем сущность метода сечений? 9. Охарактеризуйте внутренние силовые факторы (внутренние силы и моменты), которые могут возникнуть в поперечном сечении бруса. 10. Что называется напряжением в данной точке сечения? Какова его единица? 11. Что такое нормальное и касательное напряжения? Как они действуют в рассматриваемых сечениях твердого тела? 12. В чем состоит задача расчета на прочность, на жесткость, на устойчивость?
Тема 2.6 Сдвиг и кручение При изучении темы следует обратить внимание на полную смысловую аналогию законов Гука при сдвиге и при растяжении (сжатии), сравнить значения модулей упругости материала при сдвиге и при продольном деформировании (жесткость любого материала при сдвиге меньше). При кручении напряжения распределяются по поперечному сечению неравномерно (в линейной зависимости от расстояния точки до полюса сечения), опасными являются все точки контура сечения. Вопросы для самоконтроля: 1. Что такое чистый сдвиг? 2. Что называется абсолютным и относительным сдвигом? 3. Напишите формулу, выражающую закон Гука при сдвиге? 4. Что такое модуль сдвига? 5. Напишите формулу зависимости между модулем продольной упругости, модулем сдвига и коэффициентом Пуассона. 6. Что называется скручивающим моментом? 7. Какой случай нагружения бруса круглого поперечного сечения называется кручением? 8. Что называется относительным углом закручивания и полным углом закручивания? 9. Какие основные допущения приняты при изучении теории кручения бруса круглого сечения? 10. Что такое крутящий момент и чему он равен в произвольном сечении скручиваемого бруса? 11. Как строится эпюра крутящих моментов? 12. Что называется жесткостью сечения бруса при кручении? 13. Напишите формулы для определения полного угла закручивания. 14. Какие напряжения возникают в поперечном сечении скручиваемого цилиндрического бруса и как они распределяются по этому сечению?
Тема 3.1 Основные положения При изучении темы основное внимание следует обратить на связь раздела «Статики сооружений» с теоретической механикой и сопротивлением материалов, а также на классификацию сооружений и их расчетные схемы. Вопросы для самоконтроля: 1. Каковы задачи статики сооружений? 2. Что такое расчетная схема сооружения? От чего зависит ее выбор? 3. Как классифицируются сооружения? Каковы основные особенности расчетных схем каждого вида сооружений? 4. Как классифицируются опоры? Какие опорные реакции могут возникнуть в каждом их типе? 5. Какие существуют виды нагрузок? 6. Как определяются расчетные нагрузки? 7. Укажите роль отечественных ученых в развитии строительной механики. Тема 3.5 Трехшарнирные арки При изучении темы необходимо уяснить принципиальное отличие арок от криволинейных балок и уметь обосновать экономическое преимущество первых перед последними тех же очертаний и пролетов при прочих равных условиях. При определении опорных реакций трехшарнирной балки надо обратить внимание на составление дополнительного уравнения для нахождения распора. В этом уравнении изгибающий момент в ключевом шарнире должен быть равен нулю. Следует усвоить, что для построения эпюр внутренних усилий от действия на арку только равномерно распределенной нагрузки надо определить эти усилия в произвольном сечении, подставляя в полученные выражения значения х, получить значения соответствующих усилий в различных (конкретных) сечениях и по этим значениям построить соответствующие эпюры, В случае действия на арку сосредоточенных сил, внутренние усилия надо определить на каждом участке обязательно в сечениях, соответствующих точкам приложения сосредоточенных сил, а также в промежуточных сечениях каждого участка. Чем чаще будут взяты промежуточные сечения, тем точнее будут построены эпюры. При небольших расстояниях между сосредоточенными силами достаточно определить значения Q, М и N в начале каждого участка, посередине и в конце его. Вопросы для самоконтроля: 1. В чем отличие распорной системы от безраспорной? 2. Каково назначение затяжки (в случае устройства арки с затяжкой)? 3. Как определить силу в затяжке? 4. По каким правилам определяют поперечные силы, изгибающие моменты и продольные силы в сечениях арки? 5. Почему для построения эпюр Qx, Мх и N при действии на арку сосредоточенных сил недостаточно определить значение этих внутренних силовых факторов в начале и конце каждого участка, чего, как известно, достаточно для построения эпюр для балок с прямой осью? 6. Каков порядок и принцип построения многоугольника и кривой давления? 7. Что такое рациональное очертание оси арки? 8. Что называется сводом? 9. В чем сходство расчета арки и свода? Тема 3.9 Неразрезные балки Степень статической неопределимости неразрезных балок рекомендуется определять по формуле Л = Соп-3, где Л — степень статической неопределимости; 3 — число уравнений статики; Соп — число опорных стержней. Следует иметь ввиду, что нумерация опор и пролетов неразрезной балки может быть произвольной. Однако в подавляющем большинстве случаев опоры принято обозначать слева направо числами 0, 1, 2,..., n—1, n, n+1 и т.д., а длину пролетов (также слева направо) — l 1, l 2,..., l n-1, l n, l n+1, и т.д. Таким образом, номер пролета совпадает с номером правой его опоры. При данной нумерации уравнение трех моментов для опоры будет иметь вид: Мn-1· l n + 2Мn (l n+ l n-1) + Мn· l n+1= - 6(ВФn + Афn+1). Если опору, для которой составляется уравнение трех моментов (опору n), назвать средней, опору n-1 — левой, n+1 — правой, пролет l n — левым, а пролет l n+1 — правым (таково их взаимное расположение), то уравнение трех моментов для рассматриваемой опоры в общем виде будет: Млев· l лев + 2Мср (l лев+ l пр) + Мпр· l пр= - 6(ВФлев + Афпр). Фиктивные опорные реакции, стоящие в правой части уравнения трех моментов, следует определить по формулам таблиц. При расчете неразрезной балки с шарнирными опорами уравнение трех моментов должно быть составлено для каждой промежуточной опоры. Если одна из опор защемлена, то ее мысленно заменяют шарнирной, добавив при этом фиктивный пролет /ф -> 0. В этом случае рассматриваемая крайняя опора становится как бы промежуточной и для нее составляется еще одно уравнение трех моментов. При составлении уравнения трех моментов надо исключать член уравнения, содержащий момент над крайней шарнирной опорой, если со стороны этой опоры нет консоли. Если же консоль имеется, то момент над крайней опорой должен входить в составляемое уравнение как известная величина, численно равная алгебраической сумме моментов всех сил, приложенных к консоли, относительно точки оси балки над этой опорой. После решения полученной системы уравнения трех моментов станут известны значения всех опорных моментов. Дальнейший расчет можно вести так, как он приведен в одном из рекомендованных учебных пособий, или пользуясь формулами для определения изгибающего момента и поперечной силы в любом сечении балки. Вопросы для самоконтроля: 1. Какой вид имеет уравнение трех моментов? Выведите это уравнение, используя каноническое уравнение метода сил. 2. Напишите уравнение трех моментов для опоры № 3 пятипролетной, четырехпролетной (без консолей), четырехпролетной (с консолью справа), трехпролетной (с защемленным правым концом) неразрезных балок при обозначении опор слева на право числами 0, 1, 2, 3 и т.д., а длин пролетов — l 1, l 2, l 3 и тд. 3. Как определяют опорные реакции неразрезных балок? 4. Объясните порядок расчета неразрезных балок. 5. Как строится суммарная эпюра изгибающих моментов? 6. Как определяется максимальный изгибающий момент в пролете с равномерно распределенной нагрузкой? 7. Какие пролеты шестипролетной неразрезной балки следует загрузить временной нагрузкой для получения максимальных значений изгибающего момента в третьем пролете, изгибающего момента над второй слева опорой, опорной реакции третьей опоры? 8. Что такое огибающая эпюра и с какой целью она строится?
Тема 3.10 Подпорные стены При изучении темы необходимо усвоить, что является активным и пассивным давлением, как оно определяется, как определяются прочность и устойчивость подпорных стен. Вопросы для самоконтроля: 1. Что называется подпорной стеной? 2. Что называется сыпучим и что идеально сыпучим телом? 3. Каково различие между углом внутреннего трения и углом естественного откоса несвязанного рыхлого грунта? 4. В чем сущность теории предельного равновесия? 5. Что называется активным и пассивным давлением? Как они определяются? 6. По какому закону изменяется давление грунта по высоте подпорной стены? 7. Что такое интенсивность давления грунта на стену и как она изменяется по высоте подпорной стены? 8. Как учитывается при расчете влияние сплошной равномерно распределенной нагрузки, находящейся в пределах призмы обрушения? 9. Каково влияние грунтовых вод на давление, воспринимаемое подпорной стеной? 10. Как проверяется устойчивость подпорных стен против сдвига и опрокидывания по методу предельных состояний? 11. Как проверяется прочность массивных подпорных стен из камня и бетона и прочность грунтового основания под подошвой фундамента по методу предельных состояний? 12. Почему под подошвой фундамента нежелательно возникновение растягивающих напряжений, хотя прочность сжатой зоны основания обеспечена? 13. От чего зависит выбор поперечного профиля подпорной стены? 14. В чем эффективность применения тонкоэлементных подпорных стен уголкового профиля?
Практическая работа № 1 Решение. 1. В задаче рассматривается равновесие тела, опирающегося на плоскость и подвешенного на нити. Заменим тело точкой 0, совпадающей с центром тяжести. 2. Приложим к точке 0 активную силу, которой является собственный вес тела G. Направим ее вниз(рис. 1, б). 3. Мысленно отбросим связи — плоскость и нить. Заменим их действие на точку 0 реакциями связей. Реакция плоскости (обозначим ее R) проходит по нормали к плоскости в точке А, а реакция или усилие в нити (обозначим ее S) — по нити от точки. Обе реакции и вес тела или линии их действия должны пересекаться в точке 0. Изобразим действующие силы в виде системы трех сходящихся сил на отдельном чертеже (рис. 1, в). 4. Выберем положение системы координат. Начало координат совмещаем с точкой 0. Ось х совмещаем с направлением линии действия реакции R, а ось у направим перпендикулярно оси х (рис. 1, г). Определим углы между осями координат и реакциями R и S. Обычно рис. 1, б и 1, в не выполняют отдельно, a сразу от рис. 1, а переходят к рис. 1, г. Можно было ось у совместить с усилием и ось х направить по углом 90°, тогда решение было бы другим. 5. Составим сумму проекций всех сил на оси координат: 1) 2) Решим систему уравнений. Из второго уравнения находим
Из первого уравнения находим
Рис. 1
6. Проверим решение, для чего расположим оси координат, как показано на рис. 1, д. Составим уравнения равновесия для вновь принятых осей: 1) 2) Решим систему уравнений способом подстановки. Из первого уравнения найдем R:
Подставим это выражение во второе уравнение:
откуда
Теперь найдем R:
Ответ: R=11,84 кН; S=22,27 кН.
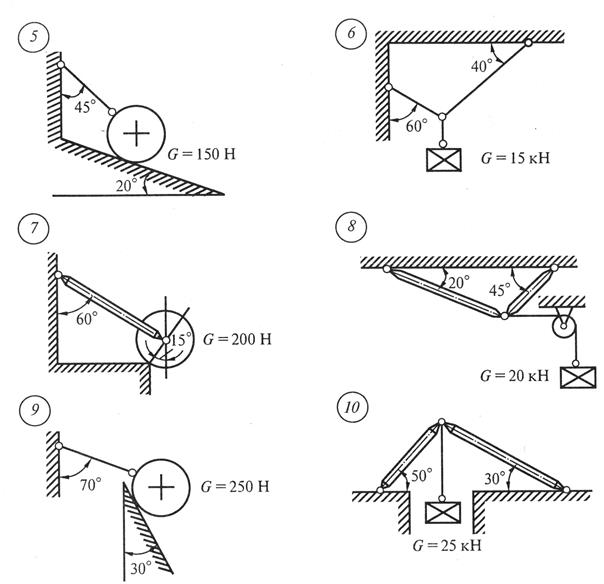
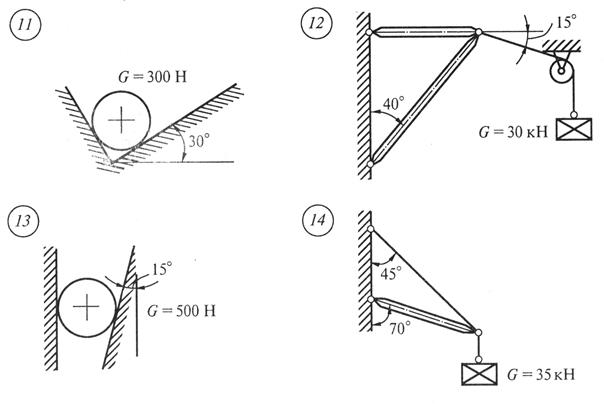
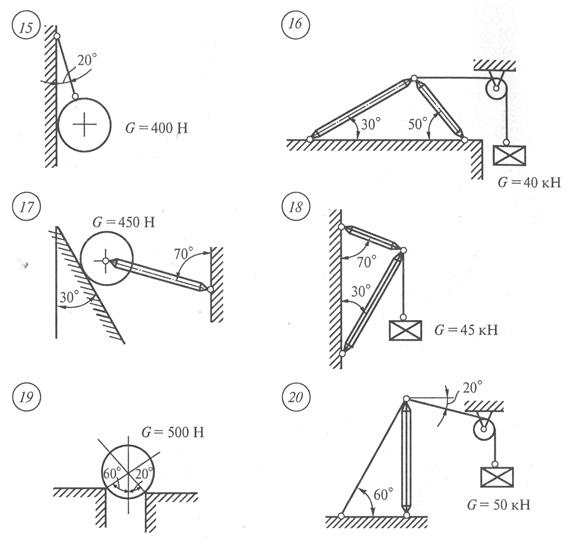
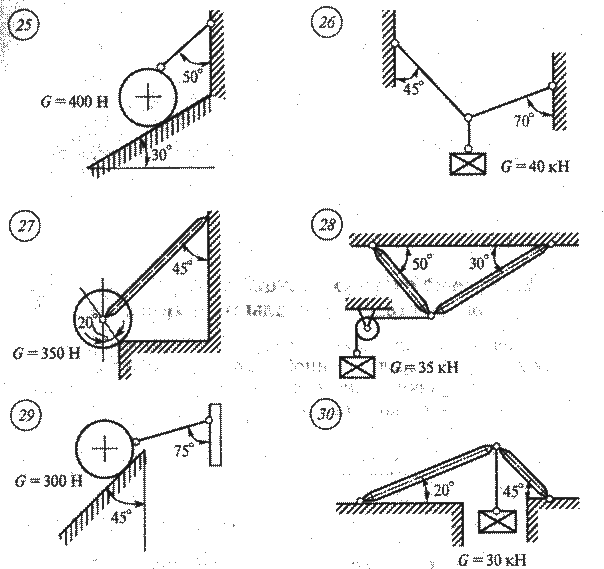
Задание для практической работы № 1. Определить величину и направление реакций связей по данным одного из вариантов, показанных на рис. 2.
Рис. 2
Рис. 2 Продолжение
Рис. 2 Продолжение
Рис. 2 Окончание Практическая работа № 2 Решение. 1. Заменяем распределенную нагрузку равнодействующей. На балку действуют нагрузки разной интенсивности, поэтому для каждой из них найдем равнодействующую:
где l1=a+b=1+3,5=4,5м; l2=d+d=1,5+1,5=3м. Укажем расстояния от этих сил до каждой из опор (рис 3, б). 2. Обозначим опоры А и В. 3. Укажем опорные реакции VA и VB. 4. Составляем уравнения равновесия. Первое уравнение примет вид:
 , ,
Рис. 3
откуда
откуда
5. Выполняем проверку, используя уравнение
или
Реакции определены правильно. Ответ: VA= 67,9 кН; VB= 37,1 кН.
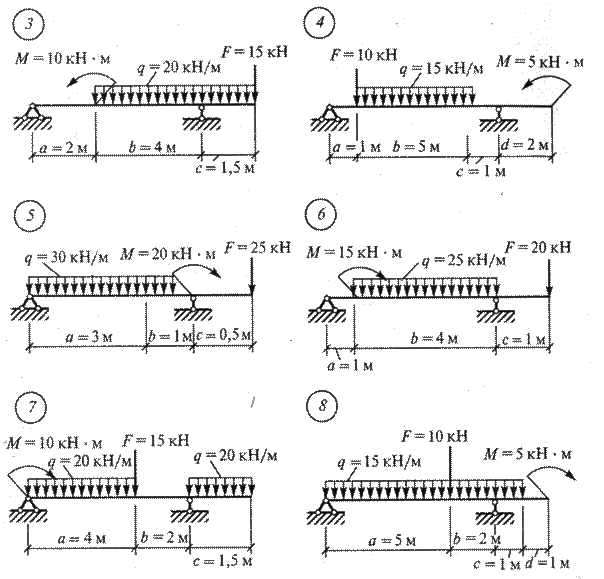
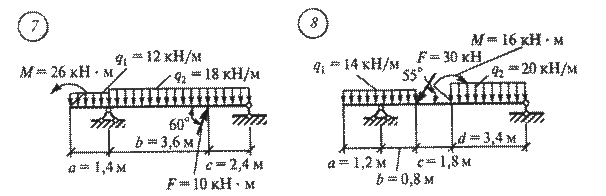
Задание для практической работы № 2. Определите опорные реакции балки по данным одного из вариантов, показанных на рис. 4.
Рис. 4
Рис. 4 Продолжение
Рис. 4 Продолжение
Рис. 4 Окончание Практическая работа № 3 Решение. 1. Освобождаемся от опор и заменяем их действие реакциями опор. 2. Определим плечо силы F1 относительно опоры A. Для этого из точки A опустим перпендикуляр на линию действия силы F1 и из треугольника ADE определим плечо силы F1:
Рис. 5
Плечо силы F1 относительно опоры B определим из треугольника BDG:
3. Составим уравнение равновесия. Первое уравнение
или
откуда Второе уравнение
или
откуда Третье уравнение
откуда Знак «минус» означает, что HA направлена в сторону, противоположно показанной на рис. 5, б. 4. Выполним проверку:
или
Ответ: VA =67,76 кН; VB =70,68 кН; НА =- 45,01 кН. Задание для практической работы № 3. Определить опорные реакции балки по одному из вариантов, показанных на рис. 6.
Рис. 6 Продолжение
Рис. 6 Продолжение
Рис. 6 Окончание Практическая работа № 4 Решение. 1. Разобьем сечение на профили проката: двутавр и швеллер. Обозначим их цифрами 1 и 2. 2. Укажем центры тяжести каждого профиля С1 и С2, используя сортамент. 3. Выберем систему осей координат. Ось х совместим с осью симметрии, а ось у проведем через центр тяжести двутавра. 4. Определим координаты центра тяжести сечения. Координата ус = 0, так как ось х совпадает с осью симметрии. Координату хс определим по формуле
По сортаменту определим
Подставим числовые значения в формулу и получим
5. Нанесем точку С (центр тяжести сечения) по найденным значениям хс и ус (см. рис. 7, а).
Рис. 7
6. Проверку решения необходимо выполнить самостоятельно при положении осей, как показано на рис. 7, б. В результате решения получим хс = 11,86 см. Разница между значениями хс при первом и втором решении равна 11,86 - 6,11 = 5,75 см, что равно расстоянию между осями у при тех же решениях bдв /2 = 5,75 см. Ответ: хс =6,11 см, если ось у проходит через центр тяжести двутавра; хс =11,86 см, если ось у проходит через левые крайние точки двутавра.
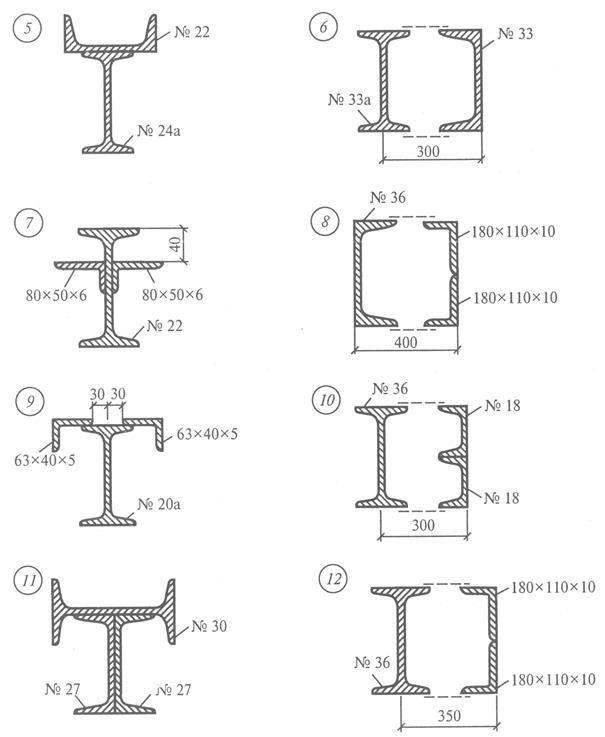
Задание для практической работы № 4. Определить координаты центра тяжести сечения по данным одного из вариантов, показанных на рис. 8. Показать положение центра тяжести на сечении.
Рис. 8
Рис. 8 Продолжение
Рис. 8 Продолжение
Рис. 8 Продолжение
Рис. 8 Окончание
Практическая работа № 5 Решение. 1. Разобьем сечение на пять фигур: два прямоугольника I и II, два треугольника III и IV и круг V. 2. Укажем центры тяжести простых фигур С1, С2, С3, С4, С5 (рис 9, б). 3. Выберем систему координат. Ось x проведем через центр тяжести С2 прямоугольника, а ось y совместим с осью симметрии сечения. 4. Определим координаты центра тяжести сечения:xC =0, т.к. ось y совпадает с осью симметрии;
Используя приложение II, определим площади фигур и координаты центров тяжести:
Рис. 9
Подставим числовые значения a формулу
Для проверки решения ось x1 можно провести по нижней грани сечения. В этом случае yC = 30,84 см. Поскольку 30,84 – 21 = 9,84 см, то решение верно. Ответ: yC = 9,84 см, если ось х проходит через центр тяжести С2. Задание для практической работы № 5. Определите положение центра тяжести сечения, состоящего из простых геометрических фигур, по данным одного из вариантов, показанных на рис. 10.
Рис. 10
Рис. 10 Продолжение
Рис. 10 Продолжение
Рис 10 Окончание
Практическая работа № 6 Решение. 1. Мысленно отбрасываем стержень, заменяя его действие на брус усилием N. Направим его вверх, полагая, что он уравновешивает нагрузку, направленную вниз. Рис. 11
2. Определим величину усилия N, составим уравнение равновесия
где После подстановки известных величин получим
откуда
3. Определим требуемую площадь поперечного сечения стержня по формуле:
где R =230 МПа для стали марки С-235 (см. прил. VIII). 4. По найденной площади определим требуемый профиль (номер) равнополочного уголка. На два уголка требуется 9,07 см2, на один - А 1=4,535 см2. По приложению I подбираем уголок 50х5 площадью 4,80 см2. На два уголка площадь А =9,6 см2. 5. Выполняем проверку прочности принятого сечения по формуле:
учитывая, что 1 МН/м2=1 МПа. Прочность стержня обеспечена, т.к. условие удовлетворительно. Ответ: Для стержня принято сечение из двух уголков 50х5.
Пример 7. Подбор сечения стержня-подвески из арматурной стали класса А-II, поддерживающего брус АВ, как показано на рис 11. Решение. 1. Мысленно отбрасываем стержень, заменяя его действие на брус усилием N. Направим его вверх, полагая, что он уравновешивает нагрузку, направленную вниз. 2. Определим величину усилия N, составим уравнение равновесия
где После подстановки известных величин получим
откуда
3. Определим требуемую площадь поперечного сечения стержня по формуле:
где R =280 МПа для арматурной горячекатаной стали класса А-II (см. прил. VIII). 4. Oпределим требуемый диаметр стержня по формуле:
Округляя полученный результат до размера, кратного 2 мм в большую сторону, получим диаметр стержня d= 32 мм или 3,2 см. 5. Выполняем проверку прочности сечения стержня: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |











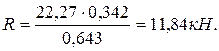




 ;
; ,
,
 Второе уравнение примет вид:
Второе уравнение примет вид: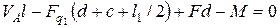 ,
, .
. , которое примет вид
, которое примет вид
 откуда 135-135=0.
откуда 135-135=0.












 ,
,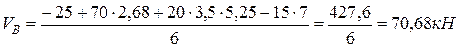 .
.
 ,
, .
. ,
, .
.







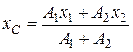 .
.








 .
.







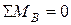 , которое примет вид
, которое примет вид ,
, .
. ,
, .
. ,
, ,
, ,
, .
.


