
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи механики. Естественный и векторный способы описания движения материальной точки (МТ)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задачи механики. Естественный и векторный способы описания движения материальной точки (МТ) Меха́ника— область физики, изучающая движение материальных тел и взаимодействие между ними. Основная задача механики – определить положение тела в любой момент времени.
Материа́льная то́чка (частица) — простейшая физическая модель в механике — идеальное тело, размеры которого равны нулю, можно также считать размеры тела бесконечно малыми по сравнению с другими размерами или расстояниями в пределах допущений исследуемой задачи. Положение точки относительно тела отсчета можно задавать естественным и векторным способами. Естественный способ описания движения МТ основывается на том что нам известна траектория движения. Зная её мы легко можем найти путь( Основные понятия кинематики. Векторный и координатный способы описания движения материальной точки. Кинематика -рассматривает движение тел без выяснения причин этого движения. Кинематика-раздел мех., в котором изучается мех движ тел независимо от причин, вызывающих и изменяющих это движ. Тело отсчёта - тело, условно принимаемое за неподвижное, относительно которого рассматривается движение др тел. Мех движение-изменение положения тел относительно др тел в пространстве с течением времени. Сист отсчёта состоит из тела отсчёта, сист координат и прибора для измерения времени. МТ- тело, размерами которого можно пренебречь в данных усл. Траектория- воображаемая линия, которую опис движущаяся МТ. 1 Координатный способ. Это наиболее универсальный и исчерпывающий способ описания движения. Он предполагает задание: а) системы координат (не обязательно декартовой) q1, q2, q3; б) начало отсчета времени t; в) закона движения точки, т.е. функций q1(t), q2(t), q3(t). Говоря о координатах точки, мы всегда будем иметь в виду ее декартовы координаты. 2. Векторный способ. Положение точки в пространстве может быть определено также и радиус-вектором, проведенным из некоторого начала в данную точку (рис. 2). В этом случае для описания движения необходимо задать: а) начало отсчета радиус-вектора r; б) начало отсчета времени t; в) закон движения точки r (t) ????3.Классификация механических движений материальной точки. Основные соотношения кинематики прямолинейного движения. Классификацию видов движения материальной точки подразделяются на два вида: прямолинейное (
Момент инерции. Примеры вычисления моментов инерции твердых тел. Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Измеряется: кг·м².Обозначается: I или J. Примеры:
Теорема Штейнера. Примеры ее применения. Если известен момент инерции тела относительно оси проходящей ч/з его центр масс то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно любой оси вращения равен моменту его инерции Jc относительно параллельной оси проходящей ч/з центр масс С тела, сложенной с произведением массы m тела на квадрат расстояния а между осями: J= Jc + ma2. Пример: Момент инерции стержня относительно оси, проходящей через его центр и перпендикулярной стержню, (назовём её осью Уравнение плоской волны. Плоская волна — волна, у которой направление распространения одинаково во всех точках пространства. Волновое уравнение. Волновое уравнение в математике — линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах (акустика, преимущественно линейная: звук в газах, жидкостях и твёрдых телах) и электромагнетизме (электродинамике). Находит применение и в других областях теоретической физики, например при описании гравитационных волн. В общем случае волновое уравнение записывается в виде Основные понятия гидродинамики. Теорема неразрывности и ее следствия. Задачи механики. Естественный и векторный способы описания движения материальной точки (МТ) Меха́ника— область физики, изучающая движение материальных тел и взаимодействие между ними. Основная задача механики – определить положение тела в любой момент времени.
Материа́льная то́чка (частица) — простейшая физическая модель в механике — идеальное тело, размеры которого равны нулю, можно также считать размеры тела бесконечно малыми по сравнению с другими размерами или расстояниями в пределах допущений исследуемой задачи. Положение точки относительно тела отсчета можно задавать естественным и векторным способами. Естественный способ описания движения МТ основывается на том что нам известна траектория движения. Зная её мы легко можем найти путь( Основные понятия кинематики. Векторный и координатный способы описания движения материальной точки. Кинематика -рассматривает движение тел без выяснения причин этого движения. Кинематика-раздел мех., в котором изучается мех движ тел независимо от причин, вызывающих и изменяющих это движ. Тело отсчёта - тело, условно принимаемое за неподвижное, относительно которого рассматривается движение др тел. Мех движение-изменение положения тел относительно др тел в пространстве с течением времени. Сист отсчёта состоит из тела отсчёта, сист координат и прибора для измерения времени. МТ- тело, размерами которого можно пренебречь в данных усл. Траектория- воображаемая линия, которую опис движущаяся МТ. 1 Координатный способ. Это наиболее универсальный и исчерпывающий способ описания движения. Он предполагает задание: а) системы координат (не обязательно декартовой) q1, q2, q3; б) начало отсчета времени t; в) закона движения точки, т.е. функций q1(t), q2(t), q3(t). Говоря о координатах точки, мы всегда будем иметь в виду ее декартовы координаты. 2. Векторный способ. Положение точки в пространстве может быть определено также и радиус-вектором, проведенным из некоторого начала в данную точку (рис. 2). В этом случае для описания движения необходимо задать: а) начало отсчета радиус-вектора r; б) начало отсчета времени t; в) закон движения точки r (t) ????3.Классификация механических движений материальной точки. Основные соотношения кинематики прямолинейного движения. Классификацию видов движения материальной точки подразделяются на два вида: прямолинейное (
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1733; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.85.79 (0.011 с.) |

 Механика где? Кинематика
Механика где? Кинематика
 почему? Динамика
почему? Динамика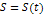 ), перемеще- ние, скорость(
), перемеще- ние, скорость(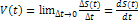 , ускорение
, ускорение 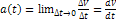 . Недостатки: необход начальные сведения о траектории, проблема двух тел. При векторном способе положение частицы по отношению к системе отсчета определяется с помощью радиус-вектора r. Траектория точки годограф вектора r, -геометрическое место концов радиус-вектора. В большинстве случаев траектория невидима и допускает лишь математическое описание. Модуль радиус-вектора равен расстоянию от траектории до начала координат.
. Недостатки: необход начальные сведения о траектории, проблема двух тел. При векторном способе положение частицы по отношению к системе отсчета определяется с помощью радиус-вектора r. Траектория точки годограф вектора r, -геометрическое место концов радиус-вектора. В большинстве случаев траектория невидима и допускает лишь математическое описание. Модуль радиус-вектора равен расстоянию от траектории до начала координат.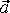 n = 0) и криволинейное (
n = 0) и криволинейное (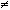 0). В зависимости от характера изменения скорости механические движения подразделяются также на два вида: равномерное (|
0). В зависимости от характера изменения скорости механические движения подразделяются также на два вида: равномерное (| 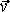 | = const,
| = const, 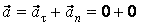 ;
; 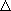
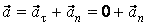 ;
; 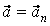 ,т.е.
,т.е. 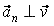 . б) Равнопеременное движение материальной точки по окружности (модуль скорости изменяется, но |
. б) Равнопеременное движение материальной точки по окружности (модуль скорости изменяется, но | 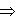
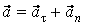 ;
; 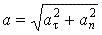 . Если направления векторов тангенциального ускорения и скорости совпадают– это равноускоренное движение материальной точки по окружности. Если направления векторов тангенциального ускорения и скорости противоположны – это равнозамедленное движение материальной точки по окружности.
. Если направления векторов тангенциального ускорения и скорости совпадают– это равноускоренное движение материальной точки по окружности. Если направления векторов тангенциального ускорения и скорости противоположны – это равнозамедленное движение материальной точки по окружности.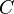 ) равен
) равен 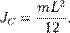 Тогда согласно теореме Штейнера его момент относительно произвольной параллельной оси будет равен
Тогда согласно теореме Штейнера его момент относительно произвольной параллельной оси будет равен 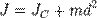 где
где 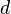 — расстояние между искомой осью и осью
— расстояние между искомой осью и осью 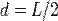 :
: 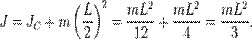
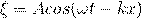 ;
; 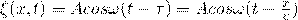 .
.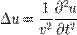 , где
, где 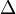 — оператор Лапласа,
— оператор Лапласа, 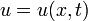 — неизвестная функция,
— неизвестная функция, 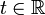 — время,
— время, 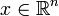 — пространственная переменная,
— пространственная переменная, 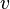 — фазовая скорость.
— фазовая скорость.


