
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение скорости и ускорения точки тела, совершающего вращательное движение.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Скорости точек тела. При вращении тела точка М будет описывать окружность радиуса h, плоскость которой перпендикулярна оси вращения, а центр С лежит на самой оси. Если за время dt происходит элементарный поворот тела на угол dφ, то точка М при этом совершает вдоль своей траектории элементарное перемещение ds=hdφ. Тогда числовое значение скорости точки будет равно отношению ds к dt, т.е
Скорость Таким образом, числовое значение скорости точки вращающегося твердого тела равно произведению угловой скорости тела на расстояние от этой точки до оси вращения. Направлена скорость по касательной к описываемой точкой окружности или перпендикулярно плоскости, проходящей через ось вращения и точку М. Так как для всех точек тела
Рис.11 Рис. 12 2. Ускорения точек тела. Для нахождения ускорения точки М воспользуемся формулами
В нашем случае ρ=h. Подставляя значение v в выражения aτ и an, получим:
или окончательно:
Касательная составляющая ускорения aτ направлена по касательной к траектории (в сторону движения при ускоренном вращении тела и в обратную сторону при, замедленном); нормальная составляющая an всегда направлена по радиусу МС к оси вращения (рис.12). Полное ускорение точки М будет
Отклонение вектора полного ускорения от радиуса описываемой точкой окружности определяется углом μ, который вычисляется по формуле
Подставляя сюда значения aτ и an, получаем
Так как ω и ε имеют в данный момент времени для всех точек тела одно и то же значение, то ускорения всех точек вращающегося твердого тела пропорциональны их расстояниям от оси вращения и образуют в данный момент времени один и тот же угол μ с радиусами описываемых ими окружностей. Поле ускорений точек вращающегося твердого тела имеет вид, показанный на рис.14.
Рис.13 Рис.14
Динамика 20.Динамика как раздел теоретической механики. Основные понятия (материальное тело, материальная точка, сила, инертность материальных тел, масса тела, система отсчета). Динамикой называется раздел теоретической механике в котором изучаются механические движения материальных тел в зависимости от причин, их вызывающих. Инерция — это явление, при котором тела сохраняют состояние покоя или равномерное прямолинейное движение при отсутствии внешних воздействий. Инерциальные системы отсчета — это такие системы отсчета, при которых выполняются условия инерции тел, то есть относительно которых тело будет двигаться прямолинейно и равномерно, если внешние воздействия будут компенсированы. Основная задача динамики — это задача установить законы движения, а также определить силы, которые действуют при этом движении. Сила F — это векторная величина, которая характеризует взаимодействие тел, в результате которого они могут изменять состоя-ние движения, а иногда даже приводит к деформации. В Международной системе единиц (в системе СИ) единицей измерения силы является ньютон и обозначается (Н). Взаимодействие — это изменение движения тел при каком- либо воздействии друг на друга. При взаимодействии определенных тел отношение ускорений, полученных ими, будет являться величиной постоянной и записывается: Инертность — это свойство тел, которое состоит в том, что что-бы изменить скорость тела, необходимо некоторое время; чем это время больше, тем инертнее тело. Масса m — это физическая величина, которая характеризует инертность тела, а также способность приобретать ускорение при взаимодействии с другими телами. 21.Основные законы динамики (Галилея-Ньютона) для точки. Понятие инерциальной системы отсчета. Две задачи динамики материальной точки. Уравнение В механике Ньютона масса не зависит от характеристик движения, времени. Записав ускорение как
Вектор Импульс это одна из важнейших динамических характеристик материальной точки В форме (**) основной закон динамики утверждает, что скорость изменения импульса материальной точки равна действующей на нее силе. В этом состоит (согласно современной терминологии) второй закон Ньютона. Основной закон динамики выражает принцип причинности в классической механике, т.е. устанавливает однозначную связь между изменением со временем состояния движения и положением материальной точки в пространстве и действующей на нее силой. Закон позволяет по начальному состоянию материальной точки: начальным координатам и скорости в начальный момент времени ( На основании обобщения опытных фактов был установлен важный принцип ньютоновской механики - принцип независимости действия сил: если на материальную точку одновременно действует несколько сил, то каждая из них, сообщает материальной точке такое же ускорение, как если бы других сил не было. Т.о.
Основной закон динамики можно переписать в виде:
Величину Т.о. из основного закона и принципа независимости действия сил следует, чтоизменение импульса материальной точки за малый промежуток времени
Интеграл в правой части есть импульс силы за конечный промежуток времени Если сила, действующая на материальную точку постоянная, то:
если
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1033; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.110.145 (0.008 с.) |


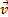 в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью точки М.
в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью точки М. имеет в данный момент времени одно и то же значение, то скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения.
имеет в данный момент времени одно и то же значение, то скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения.






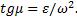


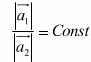
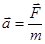 описывает изменение движения тела конечных размеров под действием силы при отсутствии деформации и если оно движется поступательно. Для точки это уравнение справедливо всегда, поэтому его можно рассматривать как основной закон движения материальной точки.
описывает изменение движения тела конечных размеров под действием силы при отсутствии деформации и если оно движется поступательно. Для точки это уравнение справедливо всегда, поэтому его можно рассматривать как основной закон движения материальной точки. и умножив на массу, получим:
и умножив на массу, получим: 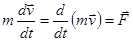 или
или (**).
(**). равный произведению массы тела на его скорость называют импульсом материальной точки.
равный произведению массы тела на его скорость называют импульсом материальной точки. ) и действующей на нее силы рассчитать ее поведение в любой последующий момент времени.
) и действующей на нее силы рассчитать ее поведение в любой последующий момент времени. , где
, где 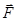 —результирующая сила;
—результирующая сила; (***)
(***) называют элементарным импульсом, вектор
называют элементарным импульсом, вектор  - элементарным импульсом силы за малый промежуток времени
- элементарным импульсом силы за малый промежуток времени 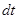 её действия.
её действия.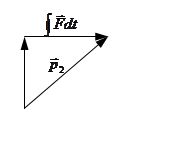 Изменение импульса за конечный промежуток времени от
Изменение импульса за конечный промежуток времени от  до
до  можно найти интегрированием левой и правой частей уравнения (***)
можно найти интегрированием левой и правой частей уравнения (***) , смотри рис..
, смотри рис..

 .
. 
 ;
;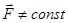 то
то  ,
,  среднее значение силы за
среднее значение силы за 


