
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение скорости и ускорения точки при различныхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте способах задания её движения
Траекторией точки называется геометрическое место последовательных положений этой точки в пространстве. Существует три способа задания движения точки: векторный, координатный и естественный. При векторном способе задания движения положение точки М определяется заданием радиуса-вектора
Выражение (1.1) является законом движения при векторном способе. Скорость точки равна первой производной от радиус-вектора точки по времени
Вектор скорости Ускорение точки равно первой производной от вектора скорости по времени или второй производной от радиус-вектора по времени
Вектор ускорения При координатном способе задания движения положение точки М в системе отсчёта Оxyz определяется тремя координатами x, y, z. При движении точки её координаты изменяются с течением времени, следовательно, они являются функциями от времени (рис. 2)
 определяются проекции скорости на оси координат как первые производные от соответствующих координат точки по времени определяются проекции скорости на оси координат как первые производные от соответствующих координат точки по времени
и направляющие косинусы вектора
Скорость точки измеряется в м/с. Проекции ускорения на оси координат равны первым производным от соответствующих проекций скорости по времени или вторым производным от соответствующих координат точки по времени
Вычислив проекции ускорения на оси координат, можно определить модуль и направление вектора ускорения
Ускорение точки измеряется в м/с2. При естественном способе задания движения точки известны (рис. 3): 1. Траектория точки АВ. 2. Начало отсчёта О с указанием положительного «+» и отрицательного «-» направлений отсчёта дуговой координаты 3. Закон изменения дуговой координаты Выражение Модуль скорости при естественном способе равен первой производной от дуговой координаты S по времени
Вектор ускорения
Касательное ускорение
Если Нормальное ускорение
где Вектор нормального ускорения Учитывая, что
Рассмотрим частные случаи движения точки: 1. Равномерное прямолинейное движение. В этом случае Тогда касательное ускорение
нормальное ускорение
так как радиус кривизны прямолинейной траектории Учитывая, что После интегрирования получаем
Выражение (1.16) является законом движения точки в рассматриваемом случае. 2. Равномерное криволинейное движение. В этом случае Тогда Ускорение точки 3. Равнопеременное прямолинейное движение. В этом случае Учитывая, что После интегрирования
где В рассматриваемом случае нормальное ускорение
В этом случае ускорение точки
4. Равнопеременное криволинейное движение. В этом случае, в отличие от рассмотренного в п. 3, 5. Общий случай движения. В этом случае
Закон движения точки
Рассмотрим переход от координатного способа к естественному. Пустьдвижения точки заданы координатным способом, т.е. известны функции (1.4). Найдем закон движения
где Подставляем значения и интегрируем выражение (1.21)
Окончательно получаем
где S 0 – дуговая координата при Введём понятие о годографе скорости точки. Точка
Если точку
являются параметрическими уравнениями годографа скорости. В главе «Кинематика точки» можно выделить два основных класса задач: - определение уравнений движения точки, её траектории, а также скорости, ускорения и радиуса кривизны траектории в заданный момент времени; - частные случаи движения точки.
Первый класс задач рассмотрим на следующем примере.
1. Найти уравнения движения в системе координат Для определения уравнений движения точки
где 2. Определить траекторию точки, построить траекторию и указать положение точки Для определения траектории точки
Возводя в квадрат эти выражения и складывая, получим уравнение траектории точки:
Находим положение точки
Указываем точку 3. Для момента времени Определяем проекции скорости точки
При Скорость точки Зная проекции скорости 4. Для момента времени Определяем проекции ускорения точки
При Ускорение точки Зная проекции ускорения 5. В момент времени Радиус кривизны определяем из выражения для нормального ускорения Нормальное ускорение
где касательное ускорение
При
Находим нормальное ускорение
Тогда радиус кривизны траектории
Покажем на рис. 6 векторы касательного ускорения Методику решения задач на частные случаи движения точки рассмотрим на следующих двух примерах. Пример 2. Точка начинает двигаться равноускоренно из состояния покоя по окружности радиусом R = 0,5 м и за первые 5 с проходит путь, равный 2 м. Определить закон движения точки по окружности, приняв за начало отсчёта начальное положение точки, а также её скорость и ускорение в конце 5 с. Для решения задачи записываем выражения, по которым определяются скорость и закон движения точки при равноускоренном движении:
По условию данной задачи Отсюда При Скорость точки при Находим нормальное ускорение точки
Ускорение точки при
Пример 3. Точка движется так, что её касательное ускорение Касательное ускорение
Интегрируем данное выражение
Отсюда С другой стороны, Интегрируя данное выражение, получаем:
Закон движения точки в данном примере Примечание. Дуговую координату
Пример 4. Точка Находим моменты времени остановки точки
Находим положения точки на траектории в моменты времени
Путь за время
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Как задаётся движение точки при векторном, координатном и естественном способах? 2. Что называется траекторией точки? 3. Как определяется скорость точки при векторном, координатном и естественном способах задания движения? 4. Как определяется ускорение точки при векторном, координатном и естественном способах задания движения? 5. Что называется годографом скорости точки?
|
||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 3969; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

 , проведенного из некоторого заданного центра О (рис. 1):
, проведенного из некоторого заданного центра О (рис. 1):
 . (1.1)
. (1.1) . (1.2)
. (1.2) . (1.3)
. (1.3) лежит в соприкасающейся плоскости траектории и направлен в сторону её вогнутости.
лежит в соприкасающейся плоскости траектории и направлен в сторону её вогнутости. . (1.4)
. (1.4) . (1.5)
. (1.5) После вычисления проекций скоростей определяются модуль и направление вектора скорости
После вычисления проекций скоростей определяются модуль и направление вектора скорости  , (1.6)
, (1.6)

 . (1.7)
. (1.7) . (1.8)
. (1.8)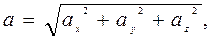 (1.9)
(1.9)

 (1.10)
(1.10)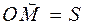 .
. .
. . (1.11)
. (1.11) Если
Если  , то вектор
, то вектор  направляем в сторону положительного отсчёта дуговой координаты S, если
направляем в сторону положительного отсчёта дуговой координаты S, если  , то – в противоположную сторону.
, то – в противоположную сторону. при естественном способе предстаёт как геометрическая сумма векторов касательного
при естественном способе предстаёт как геометрическая сумма векторов касательного  и нормального
и нормального  ускорений
ускорений . (1.12)
. (1.12)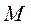 . Касательное ускорение
. Касательное ускорение  по времени или второй производной от дуговой координаты
по времени или второй производной от дуговой координаты  по времени
по времени . (1.13)
. (1.13) , то вектор
, то вектор  , то – в противоположную сторону.
, то – в противоположную сторону. , (1.14)
, (1.14) – радиус кривизны траектории в точке M.
– радиус кривизны траектории в точке M. ,модуль ускорения точки:
,модуль ускорения точки: . (1.15)
. (1.15) .
. , так как
, так как  ;
; ,
,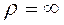 . Значит, согласно выражению (1.15), ускорение точки
. Значит, согласно выражению (1.15), ускорение точки 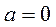 .
. ,
,  .
. ,
, . (1.16)
. (1.16) .
. ;
;  .
. , т.е. по модулю и направлению совпадает с нормальным ускорением
, т.е. по модулю и направлению совпадает с нормальным ускорением  (знак «+» соответствует ускоренному движению точки, знак «–» соответствует замедленному движению).
(знак «+» соответствует ускоренному движению точки, знак «–» соответствует замедленному движению). ,
,  .
. получается
получается , (1.17)
, (1.17) – скорость при
– скорость при  . Выражение (1.17) определяет закон изменения скорости в этом случае.
. Выражение (1.17) определяет закон изменения скорости в этом случае. , так как
, так как 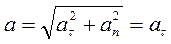 , т.е. по модулю и направлению совпадает с касательным ускорением
, т.е. по модулю и направлению совпадает с касательным ускорением  . (1.18)
. (1.18) , ускорение
, ускорение  . Тогда закон изменения скорости определяется выражением
. Тогда закон изменения скорости определяется выражением . (1.19)
. (1.19) . (1.20)
. (1.20)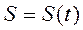 . Дифференциал дуги равен
. Дифференциал дуги равен (1.21)
(1.21) ,
,  ,
,  – дифференциалы координат точки:
– дифференциалы координат точки:  ,
,  ,
,  .
. .
. , (1.22)
, (1.22) .
. (рис. 4), занимаетна ней последовательные положения
(рис. 4), занимаетна ней последовательные положения  . Скорость точки в этих положениях равна соответственно
. Скорость точки в этих положениях равна соответственно 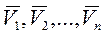 .
. Выбираем в пространстве некоторую точку
Выбираем в пространстве некоторую точку 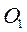 и откладываем от этой точки векторы, геометрически равные скоростям
и откладываем от этой точки векторы, геометрически равные скоростям  , то уравнения
, то уравнения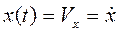 ,
,  ,
,  (1.23)
(1.23) Пример 1. Кривошип
Пример 1. Кривошип  м кривошипно-ползунного механизма (рис. 5) вращается вокруг оси
м кривошипно-ползунного механизма (рис. 5) вращается вокруг оси  по закону
по закону  (
( – в радианах,
– в радианах,  – в секундах). Для точки
– в секундах). Для точки  и
и  :
: .
. и
и  )в системе отсчёта
)в системе отсчёта  ,
,  ,
, – выражены в метрах.
– выражены в метрах. с.
с.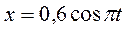 ,
,  исключить параметр времени
исключить параметр времени  ;
;  .
. .
.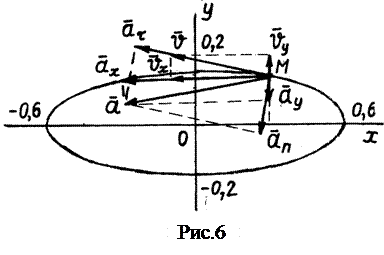 Таким образом, траектория точки
Таким образом, траектория точки  ,
,  .
. ,
,  .
. ;
;  .
.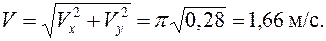
 и
и  при
при  ,
,  .
. с
с  м/с²,
м/с²,  .
. .
. и
и  , строим вектор ускорения
, строим вектор ускорения  с найти радиус кривизны траектории
с найти радиус кривизны траектории  , откуда
, откуда  .
. ,
, .
. .
. .
. .
. ;
;  .
. ,
,  .
. ,
,  .
. с
с  м. Тогда
м. Тогда  .
. .
. .
. .
. . Определить закон её движения, если при
. Определить закон её движения, если при  и
и  .
. , откуда
, откуда  .
.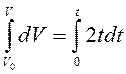 .
. (м/с).
(м/с). . Значит,
. Значит,  .
. .
. (м).
(м). (рис. 3) не следует путать с проходимым точкой расстоянием. Путь
(рис. 3) не следует путать с проходимым точкой расстоянием. Путь  за время
за время  ,
,  с.
с.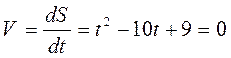 .
. Корни полученного квадратного уравнения
Корни полученного квадратного уравнения ;
; с;
с; с.
с. ,
,  ;
; с,
с,  ;
; с,
с,  ;
; с,
с,  .
. .
.


