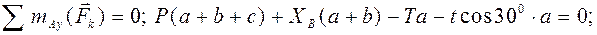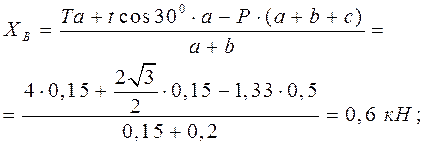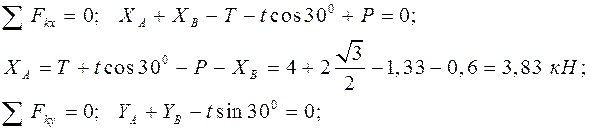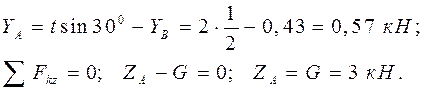Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Вариньона о моменте равнодействующейСодержание книги
Поиск на нашем сайте
Пространственная система сил приведена к равнодействующей
Согласно выражению (2.13),
Окончательно получается
Равенство (2.30) выражает теорему Вариньона о моменте равнодействующей относительно центра. Момент равнодействующей пространственной системы сил относительно любого центра А равен геометрической сумме моментов всех сил относительно этого центра. Спроектировав векторное равенство (2.30) на координатные оси, например на ось Ox, получаем выражение (2.31) теоремы Вариньона о моменте равнодействующей относительно оси:
Момент равнодействующей Частный случай теоремы Вариньона для плоской системы сил. Так как для плоской системы сил моменты на плоскости суммируются алгебраически (см. выражение (2.9)), то теорема Вариньона о моменте равнодействующей
Момент равнодействующей плоской системы сил относительно любого центра А равен алгебраической сумме моментов всех сил относительно этого центра.
Системы статически определимые И статически неопределимые
При действии на тело различных систем сил можно составить различное число уравнений равновесия. Так, для пространственной системы сходящихся сил можно составить три уравнения, для плоской системы сходящихся сил – два, пространственной системы пар – три, плоской системы пар – одно, плоской произвольной системы сил – три, плоской системы параллельных сил – два, пространственной произвольной системы сил – шесть, пространственной системы параллельных сил – три. Механические системы, в которых число неизвестных равно числу уравнений равновесия для данной системы сил, называются статически определимыми (статически определённые задачи). Механические системы, в которых число неизвестных превышает число уравнений равновесия для данной системы сил, называются статически неопределимыми (статически неопределённые задачи). Разница между числом неизвестных N и числом уравнений равновесия n для данной системы сил даёт степень статической неопределимости данной системы
Пример 1
На трёхшарнирную арку (рис. 45) действует плоская система сил
Примеры решения задач на плоскую систему сил
Пример 1 На плоскую конструкцию ABCD (рис. 46а), состоящую из горизонтального стержня AB = a, вертикального стержня BC = b в полуокружности радиуса r, действуют вертикальная равномерно распределённая нагрузка Определить реакции заделки A. Решение 1. Объект равновесия – рама ABCD (рис. 46б). 2. Активные силы: а)
б)
в) Поскольку
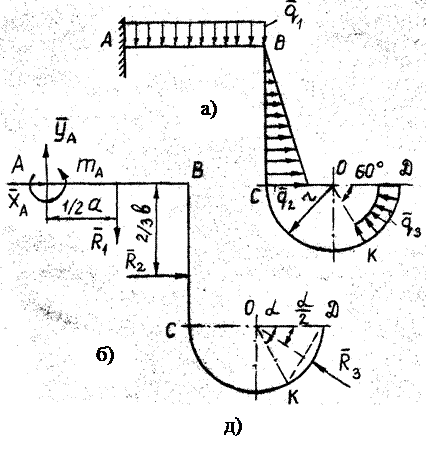
Реакции связей: 3. На раму действует плоская произвольная система сил. Составляем три уравнения равновесия:
Пример 2
Решение Конструкция состоит из двух балок АВ и ВD. Для определения реакций в заделке А, шарнире В и катковой опоре С надо составить шесть уравнений равновесия. Объекты равновесия системы можно выбирать двумя способами: 1. Всю конструкцию в целом и далее любую балку (либо АВ, либо BD). 2. Разрезать конструкцию по внутреннему шарниру В и отдельно рассмотреть балки АВ и ВD. Эта задача будет решаться более рационально, если воспользоваться вторым способом выбора объекта равновесия. Объект равновесия – левая балка ВD (рис. 48а). Активные силы: На балку BD действует плоская произвольная система сил. Составляем три уравнения равновесия:
откуда
Объект равновесия – правая балка AB (рис. 48б).
Реакции связей: На балку AB действует плоская произвольная система сил. Составляем три уравнения равновесия:
 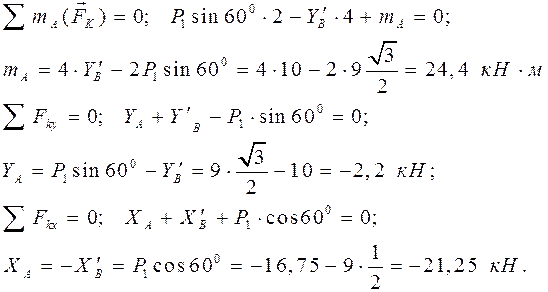
Так как реакции
Примеры решения задач на пространственную систему сил
Пример 1 На пространственную конструкцию (рис. 49а), конец которой жёстко заделан, действует вертикальная сила
Решение 1. Объект равновесия – вся конструкция (рис. 49б). 2. Активные силы:
3. На конструкцию действует пространственная система сил. Составляем шесть уравнений равновесия:
Пример 2
Решение 1. Объект равновесия – вся конструкция (рис. 50б). 2. Активные силы: Реакции связей: 3. На конструкцию действует пространственная произвольная система сил. Составляем шесть уравнений равновесия:
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется моментом силы относительно точки? 2. Как направлен вектор момента силы относительно точки и как определяется его модуль? 3. В каком случае момент силы относительно данной точки равен нулю? 4. Как определяется числовое значение и знак момента силы относительно оси? 5. При каких условиях момент силы относительно оси равен нулю? 6. Какая зависимость существует между моментом силы относительно точки и моментом той же силы относительно оси, проходящей через эту точку? 7. Каковы аналитические выражения моментов силы относительно координатных осей? 8. Какая система сил называется парой сил? 9. Как определяется численное значение и знак момента пары сил? 10. Как читаются теоремы об эквивалентных парах? 11. Каковы условия равновесия системы пар сил, расположенных в одной плоскости и в пространстве? 12. Как читается лемма Пуансо о параллельном переносе силы? 13. Как читается теорема о приведении пространственной произвольной и плоской систем сил к одному центру? 14. Что называется главным моментом системы сил относительно данной точки? 15. В чём выражаются геометрические условия равновесия пространственной системы сил? 16. Назовите аналитические условия равновесия пространственной произвольной и пространственной системой параллельных сил, плоской произвольной и плоской системой параллельных сил? 17. Какие механические системы называются статически определимыми и статически неопределимыми? 18. Как читаются теоремы о моменте равнодействующей пространственной произвольной системы сил относительно точки и оси?
|
||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 1349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.008 с.) |

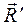 в точке О (рис. 43), значит, главный момент системы сил
в точке О (рис. 43), значит, главный момент системы сил 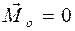 .
.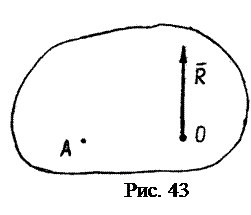 Тогда, согласно выражению (2.29), главный момент этой системы относительно нового центра А равен
Тогда, согласно выражению (2.29), главный момент этой системы относительно нового центра А равен 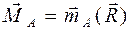 .
.
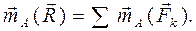 (2.30)
(2.30)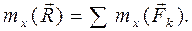 (2.31)
(2.31)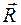 относительно оси равен алгебраической сумме моментов всех сил относительно этой оси.
относительно оси равен алгебраической сумме моментов всех сил относительно этой оси.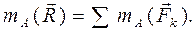 (2.32)
(2.32)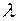
 (2.33)
(2.33)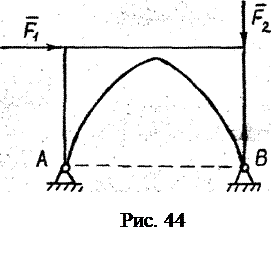 На двухшарнирную арку (рис. 44) действует плоская система сил. Неизвестных N в этой задаче – 4 (по два в каждом шарнире А и В). Уравнений равновесия n для плоской произвольной системы сил – 3. Задача статически неопределённая. Степень статической неопределимости согласно выражению (2.33)
На двухшарнирную арку (рис. 44) действует плоская система сил. Неизвестных N в этой задаче – 4 (по два в каждом шарнире А и В). Уравнений равновесия n для плоской произвольной системы сил – 3. Задача статически неопределённая. Степень статической неопределимости согласно выражению (2.33) 
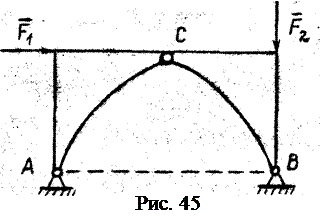 Пример 2
Пример 2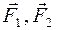 . Неизвестных N в этой задаче – 6 (по два в каждом шарнире А, B, С). Уравнений равновесия n – 6 (по три для каждой части арки АС и СВ). Задача статически определённая.
. Неизвестных N в этой задаче – 6 (по два в каждом шарнире А, B, С). Уравнений равновесия n – 6 (по три для каждой части арки АС и СВ). Задача статически определённая. , горизонтальная нагрузка
, горизонтальная нагрузка 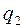 , меняющаяся по закону треугольника, и на дуге DK с центральным углом DOK = 60° радиальная распределённая нагрузка
, меняющаяся по закону треугольника, и на дуге DK с центральным углом DOK = 60° радиальная распределённая нагрузка  .
. – равнодействующая нагрузки
– равнодействующая нагрузки 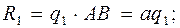
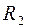 – равнодействующая нагрузки на участке BC, меняющейся по закону треугольника, численно равна площади этого треугольника
– равнодействующая нагрузки на участке BC, меняющейся по закону треугольника, численно равна площади этого треугольника
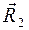 приложена в центре тяжести треугольника;
приложена в центре тяжести треугольника; – равнодействующая нагрузки
– равнодействующая нагрузки  направлена по биссектрисе угла
направлена по биссектрисе угла  и по модулю
и по модулю 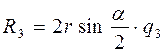 .
.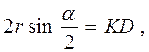 где KD – хорда, то
где KD – хорда, то 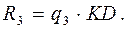
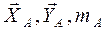 .
.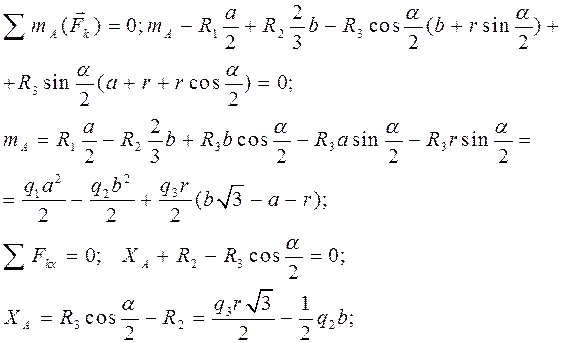
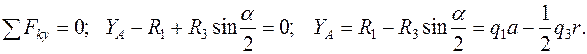
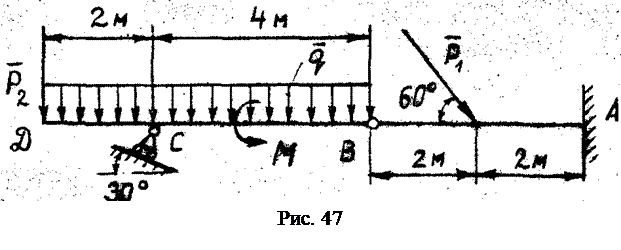 Найти реакции опор A и C и давление в промежуточном шарнире B составной конструкции, если P 1=9 кН, P 2=10 кН, M =29 кН·м, q = 1,5 кН/м (рис. 47).
Найти реакции опор A и C и давление в промежуточном шарнире B составной конструкции, если P 1=9 кН, P 2=10 кН, M =29 кН·м, q = 1,5 кН/м (рис. 47).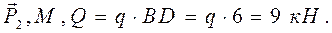 Реакции связей:
Реакции связей: 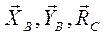 .
.
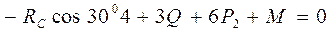 ,
,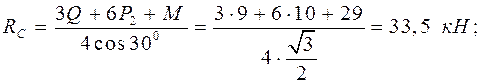
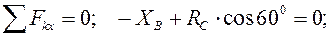
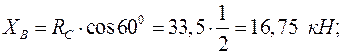

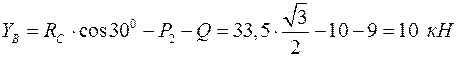 .
. Активные силы:
Активные силы: 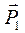 .
.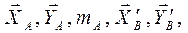 причём
причём 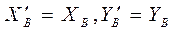 . Составляющие реакции
. Составляющие реакции 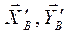 направлены против
направлены против  (аксиома: действие равно противодействию).
(аксиома: действие равно противодействию).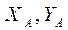 получились со знаком "минус", то действительные направления этих реакций противоположны указанным на рис. 48б направлениям.
получились со знаком "минус", то действительные направления этих реакций противоположны указанным на рис. 48б направлениям.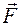 , пара с моментом М в плоскости, параллельной координатной плоскости yAz, и распределённая нагрузка в той же плоскости интенсивностью q, изменяющаяся по закону треугольника. Пренебрегая весом конструкции, определить момент MA и реакцию RA заделки.
, пара с моментом М в плоскости, параллельной координатной плоскости yAz, и распределённая нагрузка в той же плоскости интенсивностью q, изменяющаяся по закону треугольника. Пренебрегая весом конструкции, определить момент MA и реакцию RA заделки.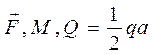 .
. Реакции связей:
Реакции связей: 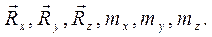

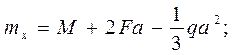

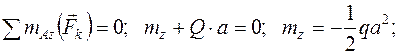
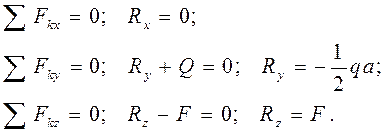
 Найти реакции опор конструкции (рис. 50а) и Р, если Т = 4 кН, G = 3 кН, а = 0,15 м, b = 0,2 м, c = 0,15 м; R = 0,15 м, r = 0,1 м, T = 2 t,
Найти реакции опор конструкции (рис. 50а) и Р, если Т = 4 кН, G = 3 кН, а = 0,15 м, b = 0,2 м, c = 0,15 м; R = 0,15 м, r = 0,1 м, T = 2 t, 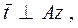
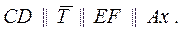
 (параллельна оси Ах),
(параллельна оси Ах), 
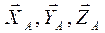 (опора А – подпятник),
(опора А – подпятник),  так как t = 0,5 T, то
так как t = 0,5 T, то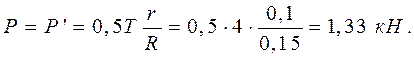
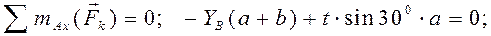
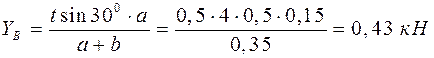 ;
;