
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Движения свободного твёрдого телаСодержание книги
Поиск на нашем сайте
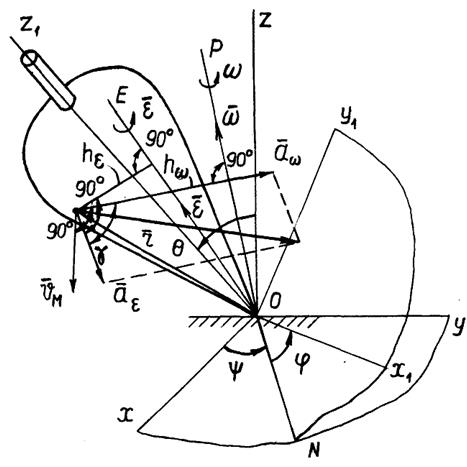
Сферическое движение совершает, например, волчок (рис. 32), у которого остаётся неподвижной точка
Поскольку для любой точки 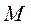 тела, совершающего сферическое движение, тела, совершающего сферическое движение,  (так как тело абсолютно твёрдое), то все точки тела движутся по сферическим поверхностям с центром в точке (так как тело абсолютно твёрдое), то все точки тела движутся по сферическим поверхностям с центром в точке  и такое движение называется сферическим. и такое движение называется сферическим.
Для изучения сферического движения вводится неподвижная система отсчета Линия Для задания положения тела при сферическом движении служат углы Эйлера:
Названия указанных углов взяты из астрономии. Выражения
называются уравнениями сферического движения твёрдого тела. Из теоремы Эйлера-Даламбера о перемещении твёрдого тела, имеющего одну неподвижную точку, следует, что сферическое движение в каждый момент времени можно рассматривать как мгновенное вращательное движение вокруг мгновенной оси Поскольку для радиус-вектора
Векторное выражение (2.32) определяет модуль и направление вектора скорости
где Из выражения (2.32) следует, что вектор скорости Представим векторное произведение (2.32) в виде определителя
где Раскладывая определитель (2.33) по элементам верхней строки, получим выражения для проекций вектора скорости
При сферическом движении твёрдого тела в общем случае направления векторов углового ускорения Ускорение точки тела при сферическом движении определяется путём дифференцирования по времени векторного выражения (2.32)
В выражении (2.35)
есть вращательное ускорение точки М тела. Из выражения (2.36) следует, что
где Вектор Вторая составляющая ускорения в выражении (2.35)
есть осестремительное ускорение точки
и вектор С учётом выражений (2.26) и (2.37) выражение (2.35) принимает вид
Равенство (2.38) выражает теорему Ривальса об ускорении точки тела, совершающего сферическое движение: ускорение любой точки тела при сферическом движении равно геометрической сумме её вращательного и осестремительного ускорений. На рис. 32 ускорение
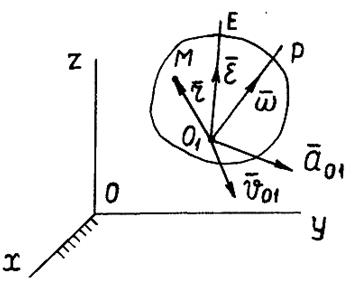 Движение свободного твёрдого тела в общем случае (рис. 33)можно представить как совокупность двух движений: поступательного вместе с некоторым полюсом Движение свободного твёрдого тела в общем случае (рис. 33)можно представить как совокупность двух движений: поступательного вместе с некоторым полюсом 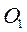 и сферического относительно полюса и сферического относительно полюса 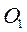 . На рис. 33 показаны . На рис. 33 показаны  , ,  – соответственно скорость и ускорение полюса; – соответственно скорость и ускорение полюса;  и и  – векторы угловой скорости и углового ускорения сферического движения. В качестве полюса может быть выбрана любая точка тела. – векторы угловой скорости и углового ускорения сферического движения. В качестве полюса может быть выбрана любая точка тела.
С учётом сказанного для свободного тела в общем случае скорость
Пример 1. Конус 1 (рис. 34а) с углом при вершине 1) угловую скорость конуса 2) угловое ускорение конуса
3) скорости низшей и высшей точек основания 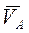 и и 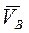 ; ;
 и и  . .
 Конус 1 движется так, что его вершина Конус 1 движется так, что его вершина 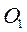 остается неподвижной, т.е. совершает сферическое движение. С другой стороны, движение конуса 1 можно рассматривать как результирующее движение от сложения вращений вокруг пересекающихся осей остается неподвижной, т.е. совершает сферическое движение. С другой стороны, движение конуса 1 можно рассматривать как результирующее движение от сложения вращений вокруг пересекающихся осей  с угловой скоростью (рис. 34б) с угловой скоростью (рис. 34б)
и оси
где
Значит,
Вектор Согласно теореме Эйлера-Даламбера, сферическое движение можно рассматривать как вращательное движение с угловой скоростью Следовательно,
где
Следовательно, мгновенная угловая скорость
Зная направление вектора Так как точка
Скорость точки
где
Следовательно,
Вектор Вектор углового ускорения
Так как модуль вектора
где Из выражения (2.42) следует, что вектор углового ускорения Из выражения (2.43) находим
из векторного произведения (2.43) следует, что вектор Находим ускорения точек
где вращательное ускорение точки
По модулю
Согласно выражению (2.42), вектор Так как точка
Значит, ускорение
Ускорение точки
где вращательное ускорение
По модулю
Из выражения (2.47) следует, что вектор
Вектор Из выражения (2.46) следует, что вектор По модулю
Пример 2. Для свободного твёрдого тела известны вектор скорости некоторой точки Скорость точки
Спроектировав векторное равенство (2.48) на неподвижные координатные оси
Зная проекции вектора
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какое движение твёрдого тела называется поступательным? 2. Как читается основная теорема поступательного движения тела? 3. Как задается движение при поступательном движении тела? 4. Какое движение твёрдого тела называют вращательным? 5. Как определяется угловая скорость и угловое ускорение при вращательном движении? 6. Как определяется и направляется скорость точки тела при вращательном движении? 7. Как определяется и направляется ускорение точки тела при вращательном движении? 8. Какое движение твёрдого тела называется плоским? 9. Как записывается уравнение плоского движения тела? 10. Как определяется скорость точки тела при плоском движении? 11. Как определяется ускорение точки тела при плоском движении? 12. Какое движение тела называется сферическим? 13. Как записываются уравнения сферического движения тела? 14. Как задаётся движение свободного твёрдого тела?
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 529; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.147.12 (0.008 с.) |

 Сферическим движением твёрдого тела называется такое движение, при котором одна точка тела остается неподвижной.
Сферическим движением твёрдого тела называется такое движение, при котором одна точка тела остается неподвижной.
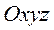 и подвижная система
и подвижная система  , которая движется вместе с телом.
, которая движется вместе с телом. пересечения неподвижной плоскости
пересечения неподвижной плоскости  с подвижной
с подвижной  называется линией узлов.
называется линией узлов.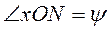 – угол прецессии;
– угол прецессии; – угол собственного вращения;
– угол собственного вращения; – угол нутации.
– угол нутации. ,
,  ,
,  (2.31)
(2.31) , проходящей через неподвижную точку
, проходящей через неподвижную точку  . Вектор угловой скорости
. Вектор угловой скорости  любой точки
любой точки  , скорости точек тела при сферическом движении можно определять по формуле Эйлера
, скорости точек тела при сферическом движении можно определять по формуле Эйлера . (2.32)
. (2.32) . Модуль равен
. Модуль равен ,
,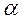 – наименьший угол между радиус-векторами
– наименьший угол между радиус-векторами  – перпендикуляр, опущенный из точки М на ось ОР.
– перпендикуляр, опущенный из точки М на ось ОР. направляется перпендикулярно плоскости МОР (значит, перпендикулярно
направляется перпендикулярно плоскости МОР (значит, перпендикулярно  , (2.33)
, (2.33)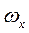 ,
,  ,
,  и
и  ,
, 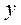 ,
,  – соответственно проекции векторов
– соответственно проекции векторов  ,
, 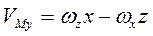 ,
,  . (2.34)
. (2.34) . (2.35)
. (2.35) (2.36)
(2.36) ,
,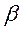 – угол наименьший между радиус-векторами
– угол наименьший между радиус-векторами 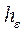 – перпендикуляр, опущенный из точки М на ось ОЕ.
– перпендикуляр, опущенный из точки М на ось ОЕ.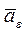 направлен перпендикулярно плоскости МОЕ (значит, перпендикулярно
направлен перпендикулярно плоскости МОЕ (значит, перпендикулярно  .
. (2.37)
(2.37)
 направлен по
направлен по  . (2.38)
. (2.38) направлено по диагонали параллелограмма, построенного на векторах
направлено по диагонали параллелограмма, построенного на векторах  между
между 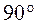 , то модуль вектора
, то модуль вектора 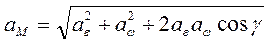 . (2.39)
. (2.39) некоторой точки
некоторой точки  , (2.40)
, (2.40) . (2.41)
. (2.41)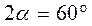 и радиусом основания AC = 0,3 м катится без скольжения по такому же неподвижному конусу 2, совершая вокруг вертикальной оси
и радиусом основания AC = 0,3 м катится без скольжения по такому же неподвижному конусу 2, совершая вокруг вертикальной оси  оборот за каждую секунду. Определить:
оборот за каждую секунду. Определить: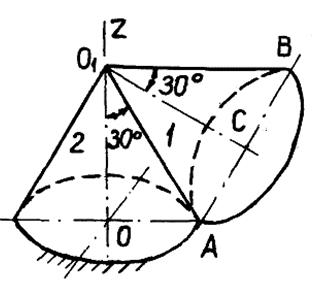


 рад/с
рад/с с угловой скоростью
с угловой скоростью  . Поскольку для точки
. Поскольку для точки  её скорость от вращения вокруг оси
её скорость от вращения вокруг оси  ,
, – перпендикуляр, опущенный из точки
– перпендикуляр, опущенный из точки  м.
м. м/с.
м/с.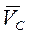 направлен перпендикулярно плоскости чертежа в сторону круговой стрелки
направлен перпендикулярно плоскости чертежа в сторону круговой стрелки  , т.е. на нас.
, т.е. на нас. , которая совпадает с образующей
, которая совпадает с образующей  конусов 1 и 2, поскольку конус 1 катится без скольжения.
конусов 1 и 2, поскольку конус 1 катится без скольжения. ,
,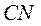 – перпендикуляр, опущенный из точки
– перпендикуляр, опущенный из точки  м.
м. рад/с.
рад/с. конуса 1 лежит на мгновенной оси
конуса 1 лежит на мгновенной оси  .
.
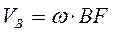 ,
, – перпендикуляр, опущенный из точки
– перпендикуляр, опущенный из точки  м.
м.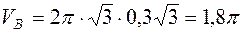 м/с.
м/с. . (2.42)
. (2.42) , то производную (3.42) можно определить по формуле Эйлера:
, то производную (3.42) можно определить по формуле Эйлера: , (2.43)
, (2.43)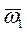 – вектор угловой скорости
– вектор угловой скорости 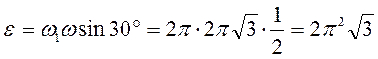 рад/с²,
рад/с², , (2.44)
, (2.44) . (2.45)
. (2.45) м/с.
м/с. направлен перпендикулярно
направлен перпендикулярно 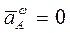 .
. .
.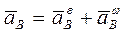 , (2.46)
, (2.46) . (2.47)
. (2.47) м/с².
м/с².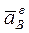 направлен вертикально вверх. Осестремительное ускорение
направлен вертикально вверх. Осестремительное ускорение м/с².
м/с². направлен по
направлен по 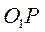 .
.

 м/с².
м/с².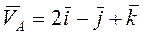 (
( – в м/с), вектор угловой скорости
– в м/с), вектор угловой скорости  (
(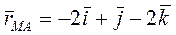 (
( – в м). Определить скорость точки
– в м). Определить скорость точки  . (2.48)
. (2.48) , получим с учётом выражений (2.34) три проекции вектора скорости
, получим с учётом выражений (2.34) три проекции вектора скорости  :
: м/с,
м/с, м/с,
м/с,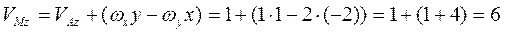 м/с.
м/с. м/с.
м/с.


