
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ГЛАВА 2. Моменты сил относительно точкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
И ОСИ. ПАРА СИЛ. ПРОСТРАНСТВЕННАЯ И ПЛОСКАЯ ПРОИЗВОЛЬНЫЕ СИСТЕМЫ СИЛ
В главе даны понятия моментов силы относительно точки и оси, изложены основные положения теории и методики решения задач на плоскую и пространственную систему сил.
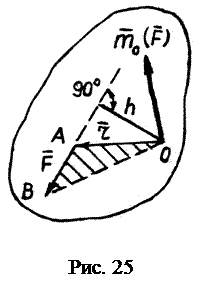
Момент силы относительно точки
Моментом силы
Точка О, относительно которой находится момент, называется моментной точкой. Плечом h силы Свойства момента силы относительно точки: 1) 2) 3)
Момент силы измеряется в системе СИ в ньютон-метрах (Н·м). При определении момента силы относительно точки в задачах часто удобно силу
Момент силы относительно точки как вектор
Вектор
Справедливо следующее векторное равенство:
где Из векторного равенства (2.3) можно определить модуль (2.2) и указанное направление вектора
Момент силы относительно оси
Момент силы
где
Из определения момента силы относительно оси следует: 1) 2) Объединяя эти два свойства, можно сказать, что Пример
Решение Для определения момента силы
Знак "минус" момента взят потому, что сила Момент силы Для определения момента силы
Знак "плюс" момента взят потому, что сила
|
||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 1671; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.80.212 (0.009 с.) |

 относительно некоторой точки О называют скалярную величину, равную взятому с соответствующим знаком произведению модуля силы
относительно некоторой точки О называют скалярную величину, равную взятому с соответствующим знаком произведению модуля силы 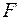 на плечо h (рис. 23):
на плечо h (рис. 23):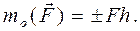 (2.1)
(2.1) Момент
Момент 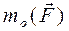 имеет знак "+", если сила
имеет знак "+", если сила 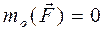 , если h = 0, т.е. если моментная точка О находится на линии действия силы;
, если h = 0, т.е. если моментная точка О находится на линии действия силы;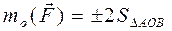 .
.
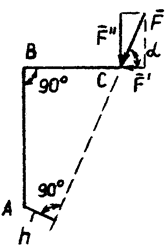 Найдём, например, момент силы
Найдём, например, момент силы 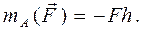 Поскольку плечо силы определять в данной задаче неудобно, представим силу
Поскольку плечо силы определять в данной задаче неудобно, представим силу 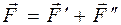 , где
, где 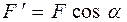 ,
, 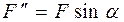 – соответственно горизонтальная и вертикальная составляющие, приложенные в той же точке С, что и сила
– соответственно горизонтальная и вертикальная составляющие, приложенные в той же точке С, что и сила 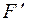 относительно точки А равно AB, силы
относительно точки А равно AB, силы 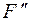 – ВС.
– ВС.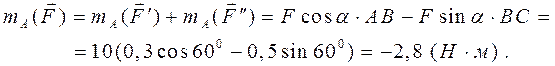
 Момент силы
Момент силы 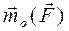 .
.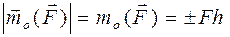 . (2.2)
. (2.2)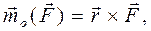 (2.3)
(2.3) – радиус-вектор, проведенный из моментной точки О в точку А приложения силы
– радиус-вектор, проведенный из моментной точки О в точку А приложения силы 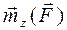 равен моменту проекции этой силы на любую плоскость, перпендикулярную оси z (например, плоскость Оху на рис. 26), относительно точки встречи оси с плоскостью – точки О:
равен моменту проекции этой силы на любую плоскость, перпендикулярную оси z (например, плоскость Оху на рис. 26), относительно точки встречи оси с плоскостью – точки О: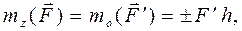
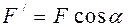 – проекция силы
– проекция силы 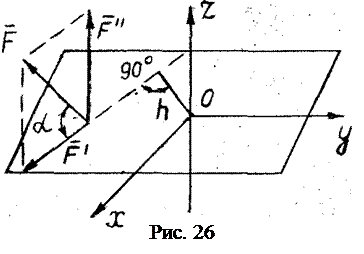 Момент силы относительно оси
Момент силы относительно оси 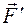 происходит против хода часовой стрелки, и отрицательным, если она стремится вращать тело по ходу часовой стрелки (если смотреть на тело с положительного направления оси Оz).
происходит против хода часовой стрелки, и отрицательным, если она стремится вращать тело по ходу часовой стрелки (если смотреть на тело с положительного направления оси Оz).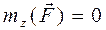 , если сила
, если сила 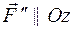 силы F момента относительно этой оси не даёт);
силы F момента относительно этой оси не даёт); По диагонали KN (рис. 27) параллелепипеда, размеры которого указаны на рис. 27, действует сила F = 10 Н. Найти моменты этой силы относительно координатных осей.
По диагонали KN (рис. 27) параллелепипеда, размеры которого указаны на рис. 27, действует сила F = 10 Н. Найти моменты этой силы относительно координатных осей. и находим момент составляющей
и находим момент составляющей 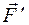 относительно точки О – точки встречи оси Ox с плоскостью Oух
относительно точки О – точки встречи оси Ox с плоскостью Oух (H×м).
(H×м). , так как сила
, так как сила  и находим момент составляющей
и находим момент составляющей  относительно точки О – точки встречи оси Oz с плоскостью Oxy
относительно точки О – точки встречи оси Oz с плоскостью Oxy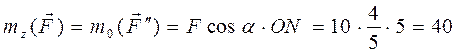 (Н×м).
(Н×м).


