
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика точки и твёрдого телаСодержание книги
Поиск на нашем сайте
ДИНАМИКА ТОЧКИ И ТВЁРДОГО ТЕЛА
__________________________________________________________ Глава 9. Динамика точки. Вопросы для самопроверки. 1. Напишите векторную формулу динамики относительного движения точки, что такое силы инерции. 2. Напишите векторную формулу силы сопротивления среды, прокомментируйте введенные обозначения. 3. Напишите в самом общем виде дифференциальные уравнения движения точки (в декартовой системе координат). 4. Напишите дифференциальные уравнения движения точки в осях натурального триэдра.
6. С какой абсолютной скоростью сойдет колечко со стержня, если его длина равна L, начальное положение 7. В чем разница между прямой и обратной (основной) задачами динамики? 8. Напишите уравнение относительного равновесия точки.. 9. Составьте дифференциальное уравнения относительного движения колечка по стержню, вращающемуся с постоянной угловой скоростью ω, трение не учитывать. 10. Чему равно время движения точки на участке горизонтального прямолинейного движения, если начальная скорость 11. Чему равен путь, пройденный точкой, на участке горизонтального прямолинейного движения, если начальная скорость Глава 10. Количество движения системы. Кинетический момент системы и твёрдого тела.
Теорема об изменении главного момента количества движения системы материальных точек. Напомним, что момент количества движения системы или кинетический момент определяется выражением
Продифференцируем написанное выражение по времени
Первое слагаемое равно нулю как векторное произведение равных векторов (ведь
В правой части первое слагаемое – главный момент внешних сил, а второе- главный момент внутренних сил, который равен нулю. Итак, окончательно имеем
Это соотношение выражает теорему об изменении кинетического момента: векторная производная по времени от главного момента количества движения системы равна главному моменту внешних сил, приложенных к системе. Равенство нулю главного момента внутренних сил приводит к заключению, что внутренние силы не могут влиять на изменение кинетического момента системы. Формула (3.21) оказываются существенно необходимой при изучении динамики вращательных движений твердого тела или системы тел. С помощью этих двух фундаментальных законов
можно получить дифференциальные уравнения движения твёрдого тела и системы тел. В разделе статика указывалось, что необходимыми и достаточными условиями равновесия являлись равенство нулю главного вектора и главного момента сил. Уравнения (3.22) можно переписать в форме, похожей на уравнения статики виде
Эти уравнения называются уравнениями кинетостатики, где индекс a обозначает активные силы и моменты активных сил, «r»– силы реакций и моменты сил реакций, а индекс «
Вопросы для самопроверки. 1. Векторная формула кинетического момента системы точек. 2. Теорема об изменении кинетического момента. 3. Дайте определения центральной и главной оси инерции. 4. Чему равен момент инерции цилиндра относительно его продольной оси симметрии? 5. Напишите векторное выражение для кинетического момента тела, вращающегося вокруг неподвижной оси (варианты- 0X, 0Y, 0Z). 6. Напишите формулу Гюйгенса. 7. Как изменится центробежный момент инерции Jyz при переходе от старой оси OZ к новой, пересекающей ось 0Y на расстоянии l. 8. Напишите формулу тензора инерции относительно выбранного центра (в диадной форме). 9. Как записать момент инерции относительно оси, заданной ортом 10. Как записать центробежный момент инерции относительно осей, заданными ортами 11. Чему равен кинетический момент относительно оси, если 12. Чему равен центробежный момент инерции относительно осей, заданными ортами
Глава 12.
Вопросы для самопроверки. 1. Напишите дифференциальное уравнение вращения тела вокруг неподвижной оси (ось вращения главная). 2. Что такое статическая и динамическая уравновешенность тела, вращающегося вокруг неподвижной оси? 3. Напишите дифференциальные уравнения плоского движения тела. 4. Напишите уравнения кинетостатики. Прокомментируйте введённые обозначения. 5 Чему равна сила трения цилиндра, катящегося по шероховатой поверхности (разберите два случая). 6. Сколько степеней свободы имеет свободное тело, какими обобщенными координатами можно описать его движение?
8.Как изменится угловая скорость вращения стержня длины L и массы M1, если груз массы М переместится из положения h на конец стержня. 9. Определите период колебаний двух стержней, показанных на рисунке, относительно горизонтальной оси.
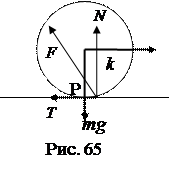
11. Как изменится центробежный момент инерции Jyz при переходе от старой оси OZ к новой, пересекающей ось 0Y на расстоянии l. 12. Определить ускорение груза и натяжение нити в указанном примере..
Глава 13. Работа силы. Мощность. Для характеристики действия силы на материальную точку на
протяжении некоторого пути вводится мера этого действия, называемая работой силы. Сначала введем в рассмотрение понятие элементарной работы (рис 61). Будем определять положение точки М на кривой
Если сила перпендикулярна к перемещению, то cosα = 0 и работа равна нулю; если сила направлена по перемещению cosα = l и работа равна произведению величины силы на величину перемещения, и, наконец, если сила направлена против движения, то cosα = - 1 и произведение уже берется со знаком минус. Таким образом, в определении работы учитывается зависимость эффекта действия силы от направления ее по отношению к перемещению. Измеряется работа в килограммометрах (кгм) в технической системе единиц, в эргах (дина см) или джоулях (
Интегрирование в полученном выражении производится по величинам, отнесенным к бесконечно малым дугам кривой Рассмотрим несколько примеров, когда вычисление работы может быть сведено к вычислению простого определенного интеграла: 1. если движение происходит по прямолинейной оси, например по оси Ох, и сила являлась функцией одного только х, то элементарная работа действительно представляет дифференциал 2. Предположим, что движение точки задано уравнениями
3. Область пространства, в каждой точке которого однозначно определена некоторая функция, будем называть полем; в зависимости от того, будет эта функция скалярной, векторной или тензорной величиной, поле будет скалярным, векторным или тензорным. Так, скалярным полем будет температурное поле, когда вокруг источника тепла (нагретого тела) в каждой точке окружающей это тело среды будет свое значение температуры. Для движущейся сплошной среды (жидкость, газ) поле скоростей точек этой среды является примером векторного поля. Примером тензорного поля может служить малая деформация среды — в каждой точке среды относительные удлинения и углы сдвига образуют некоторый тензор, называемый тензором малых деформаций. Силовым полем называется область пространства, в каждой точке которой определен вектор силы
где оператор «набла»
Здесь П = П(x, у, z) - потенциальная энергия (или потенциал) силового поля. Тогда
а это, в свою очередь, означает, что дифференциальная форма (элементарная работа)
в рассматриваемом случае будет полным дифференциалом. Итак, элементарная работа потенциальной силы является полным дифференциалом. Интегрируя соотношение (3.92) на конечном участке движения точки (от
Правая часть полученного выражения зависит только от положения (координат) начальной и конечной точек и, следовательно, работа в потенциальном силовом поле не зависит от вида пути. Рассмотрим поверхность равного потенциала П (х, у, z) = const. Сила
Мощность равна скалярному произведению векторов силы и скорости. За единицу мощности можно принять любую единицу работы, отнесенную к единице времени, т. е. эрг/сек, джоуль/сек, кГм/сек; обычно за единицу мощности принимают следующие единицы: 1 ватт= 1 киловатт =103 ватт= 1 кГ м/сек =9,807 ватт, 1 л. с. (HP) = 75 кГ м/сек = 0,736 киловатт. Иногда принято работу измерять в единицах мощности, умноженных на единицу времени, т.е. в ватт • сек, в киловатт-часах и т.п.
Примеры вычисления потенциальной энергии и работы Сил.
И в этом случае П =
2. Потенциальная энергия упругой деформации. Здесь будет исследован случай линейной теории упругости, когда материал подчиняется закону Гука. Рассмотрим упругую пружину длины Fx =- сx, Fy = Fz = 0, но
Произвольная постоянная в выражении (3.93) отброшена, так как потенциальная энергия деформации недеформированной пружины, естественно, принимается равной нулю. В эту же схему укладывается решение задачи о продольной деформации (растяжении или сжатии) призматического стержня. Появляющиеся при нагружении стержня продольными силами N нормальные напряжения
Координатой х здесь является удлинение стержня
При изгибе балки за координату х принимается прогиб f в некоторой точке, а жесткость с зависит от размеров пролета, расположения внешней нагрузки и условий закрепления балки. Так, для балки на двух шарнирных опорах, нагруженной посредине пролета сосредоточенной силой Р, жесткость следует вычислять по формуле При кручении круглого цилиндра имеет место аналогичный результат. Пусть к торцам сплошного цилиндра из упругого материала приложены крутящие моменты М; размеры цилиндра: длина
Интегрируя последнее соотношение, получаем потенциальную энергию кручения круглого стержня в виде В приведенных примерах поведение упругой системы описывалось одной координатой; возможны и более сложные (случаи, например, при одновременном растяжении, изгибе и кручении консольного стержня потенциальная энергия выражается соотношением
3. Работа сил, приложенных к твёрдому телу. Пусть силы
Второе слагаемое, согласно свойству скалярно-векторного произведения, может быть переписано в виде
Элементарная работа всех сил будет
Обозначая через - главный вектор системы сил, через
В частном случае поступательного движения твердого тела В случае плоского движения твердого тела имеем
где через 4. Работа внутренних сил, приложенных к твердому телу, выражается через главный вектор и главный момент этих сил. Работа внутренних сил взаимодействия частиц твердого тела равна нулю, так как главный вектор и главный момент этих сил равны нулю.
 жение для элементарной работы жение для элементарной работы
В этой формуле
Если диск катится без скольжения, т.е. мгновенный центр скоростей находится в нижней точке диска, то
Вопросы для самопроверки. 1. Сформулируйте теорему Кенига. 2. Кинетическая энергия тела при плоском движении (две формулы). 3. Чему равна кинетическая энергия катящегося однородного цилиндра? 4. Напишите формулу работы упругой силы. 5. Напишите формулу работы сил, приложенных к твердому телу (общий случай). 6. Напишите формулу кинетической энергии тела в самом общем случае (через тензор инерции). 7. Теорема об изменении кинетической энергии (две формулировки). 8. Какой путь пройдет центр однородного цилиндра, катящегося по наклонной плоскости, чтобы его скорость возросла в два раза, Коэффициент трения качения равен К. Радиус цилиндра R, угол наклона плоскости α. 9. Чему равна потенциальная энергия физического маятника, состоящего из кольца радиуса -- R, массы m1 и стержня длины l массы m2, если он отклонен от вертикали на угол φ. 10. Чему равна кинетическая энергия тела, вращающегося вокруг неподвижной точки, если 11. По каким формулам вычисляется работа сил, приложенных к твердому телу при: поступательном движении, вращении тела вокруг неподвижной оси, плоском движении?
РАЗДЕЛ ЧЕТВЁРТЫЙ
Возможные перемещения.
Обобщенные координаты При формулировании общих положений механики оказывается полезным ввести в рассмотрение бесконечно малые величины иной природы. Отвлекаясь от движения, зададимся вопросом, какое множество конфигураций в этот момент времени допускают связи системы. Если ограничиться рассмотрением конфигураций бесконечно близких к истинным и через
где в случае голономной системы вариации Рассмотрим точку системы
представляющим бесконечно малое перемещение точки
Если связи не зависят от времени, то в выражении (4.2) отпадает последнее слагаемое. Дифференциалы
принадлежит множеству виртуальных или возможных перемещений. В случае же нестационарных связей сравнение выражений (4.2) и (4.3) показывает, что
а вариация
- бесконечно малое изменение, обусловленное переходом в фиксированный момент времени к бесконечно близкой конфигурации системы. Рассмотренный в этом параграфе способ варьирования, заключающийся в сравнении конфигураций системы, допускаемых связями, и фиксированный момент времени t, называется синхронным варьированием. Можно рассмотреть более общую операцию асинхронного варьирования, когда истинная конфигурация в момент t сравнивается с бесконечно близкой, допускаемой связями в момент В механике Лагранжа основным понятием являются возможные перемещения, т.е. любые бесконечно малые перемещения системы, допускаемые связями, которые есть вариации координат или функций. Как указывалось выше дифференциал функции и вариация функции не одно и тоже. Уже само понятие вариация, очевидно, относится к особому методу вычисления, которое и носит название вариационное исчисление, о нём и пойдёт речь ниже. Кроме задач определения экстремальных значений функций одной или нескольких переменных в технике, экономике и в различных областях науки нередко приходится иметь дело с нахождением минимальных или максимальных значений величин особого типа, которые называются функционалами.
Приведем несколько примеров. Функционалом является длина
и, действительно, зависит от функции у(х). Отметим здесь, что функционалом является и длина пространственной кривой. Примером несколько иного типа является время движения управляемого объекта, зависящее как от формы траектории, так и от управляющего воздействия. Вариационное исчисление изучает методы, с помощью которых могут быть найдены минимальные или максимальные значения функционалов. Задачи, в которых нужно найти минимум или максимум функционала, называются вариационными задачами. Многие законы физики сводятся к утверждению, что некоторый функционал в изучаемом процессе имеет максимум или минимум. В таком виде эти законы носят название вариационных принципов физики. В качестве примеров можно привести принцип наименьшего действия Гамильтона—Остроградского в механике, принцип Ферма в оптике, различные вариационные принципы классической и релятивистской теории поля и многие другие законы физики. Начало созданию вариационного исчисления положили исследования решений задачи о брахистохроне, сформулированной И.Бернулли (1667—1748 гг.) в 1696 году. Он предложил математикам задачу о линии быстрейшего ската. В ней надо найти соединяющую две точки не лежащую на одной вертикали линию, обладающую тем свойством, что точка скатится из точки Вариационное исчисление оформилось в самостоятельную математическую дисциплину со своими методами исследования благодаря фундаментальным работам действительного члена Петербургской Академии наук Леонарда Эйлера (1707—1783 гг.). Л. Эйлера можно считать создателем вариационного исчисления. В чём разница нахождения экстремума гладкой функции одной переменной и экстремума функционала вида
после подстановки функции
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 523; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.015 с.) |


 5. Сколько (и какие) необходимо задать начальных условий для определения движения точки (в декартовой системе координат)?
5. Сколько (и какие) необходимо задать начальных условий для определения движения точки (в декартовой системе координат)?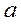 , угловая скорость вращения стержня ω. Стержень перпендикулярен оси вращения.
, угловая скорость вращения стержня ω. Стержень перпендикулярен оси вращения. , а конечная
, а конечная 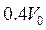 ? Сила сопротивления среды равна
? Сила сопротивления среды равна  .
.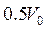 ? Сила сопротивления среды равна
? Сила сопротивления среды равна  .
. ,
,
 ), а второе, с учётом (3.14) получается равным
), а второе, с учётом (3.14) получается равным
 (3.21)
(3.21)
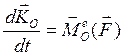 (3.22)
(3.22)

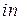 »- силы инерции и моменты сил инерции, которые равны
»- силы инерции и моменты сил инерции, которые равны ,
,  .
. , если известен тензор инерции (в общем виде).
, если известен тензор инерции (в общем виде).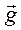 , если известен тензор инерции (в общем виде).
, если известен тензор инерции (в общем виде). , а тензор инерции
, а тензор инерции  .
.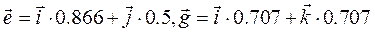 , тензор инерции
, тензор инерции  .
.
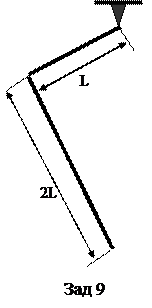 7. Чему равна приведённая длина однородного стержня длины l, колеблющегося вокруг горизонтальной оси (разберите разные случаи крепления оси: в конце стержня, на расстоянии 1/4 l от конца стержня и т.д.)
7. Чему равна приведённая длина однородного стержня длины l, колеблющегося вокруг горизонтальной оси (разберите разные случаи крепления оси: в конце стержня, на расстоянии 1/4 l от конца стержня и т.д.) 10. Напишите формулу Гюйгенса.
10. Напишите формулу Гюйгенса.
 дугой s, отсчитываемой от точки
дугой s, отсчитываемой от точки  . Вектор-радиус
. Вектор-радиус  точки М будет вектор-функцией
точки М будет вектор-функцией  от s. Работа силы
от s. Работа силы 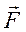 на этом элементарном перемещении, или элементарная работа
на этом элементарном перемещении, или элементарная работа  определится выражением
определится выражением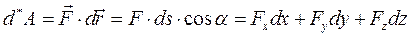
 эргов) - в физической системе. В общем же случае выражение
эргов) - в физической системе. В общем же случае выражение  не представляет полного дифференциала и символ
не представляет полного дифференциала и символ  следует понимать только как символ бесконечно малой величины, а отнюдь не дифференциала. В дальнейшем будет выяснено наличие частных классов сил, элементарная работа которых является полным дифференциалом некоторой функции от координат точки. Работа силы на конечном перемещении
следует понимать только как символ бесконечно малой величины, а отнюдь не дифференциала. В дальнейшем будет выяснено наличие частных классов сил, элементарная работа которых является полным дифференциалом некоторой функции от координат точки. Работа силы на конечном перемещении  определиться интегралом
определиться интегралом
 . Поэтому этот интеграл называется криволинейным интегралом, взятым вдоль дуги кривой
. Поэтому этот интеграл называется криволинейным интегралом, взятым вдоль дуги кривой  от точки
от точки  . Такие интегралы (они называются криволинейными) часто встречаются в различных вопросах механики, гидродинамики и электродинамики.
. Такие интегралы (они называются криволинейными) часто встречаются в различных вопросах механики, гидродинамики и электродинамики. .
. и, кроме того, задан закон изменения силы в зависимости от изменения времени, координат и скорости. Тогда, написав выражение элементарной работы через проекции силы и перемещения на оси и подставив их выражения через время t, получим
и, кроме того, задан закон изменения силы в зависимости от изменения времени, координат и скорости. Тогда, написав выражение элементарной работы через проекции силы и перемещения на оси и подставив их выражения через время t, получим  ,где Ф (t) - известная функция времени. Чтобы найти работу на пути
,где Ф (t) - известная функция времени. Чтобы найти работу на пути 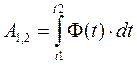 , где
, где  - моменты, соответствующие прохождению движущейся точкой положений
- моменты, соответствующие прохождению движущейся точкой положений  и
и  . Задача свелась к вычислению определенного интеграла по аргументу t.
. Задача свелась к вычислению определенного интеграла по аргументу t. , действующий на помещаемое в эту точку материальное тело. Силовое поле называется потенциальным, если сила представляет собой градиент скалярной функции. Рассмотрим свойства потенциальных силовых полей. По определению
, действующий на помещаемое в эту точку материальное тело. Силовое поле называется потенциальным, если сила представляет собой градиент скалярной функции. Рассмотрим свойства потенциальных силовых полей. По определению , (3.91)
, (3.91) в декартовой системе координат равен
в декартовой системе координат равен

 (3.92)
(3.92)
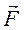 направлена по нормали к поверхности равного потенциала; знак «минус» в формуле (3.91) указывает, что потенциальная сила направлена в сторону убывания потенциальной энергии. Надо отметить, что потенциальная энергия была введена дифференциальным путём и поэтому определена с точностью до аддитивной постоянной; эта постоянная будет зафиксирована, если условиться об отсчёте потенциальной энергии от некоторого начального уровня. Желая охарактеризовать работу с точки зрения времени, в течение которого она производится, вводят понятие мощности, как отношения произведенной работы к протекшему времени или как работу, отнесенную к единице времени. Обозначая мощность через N, можем написать:
направлена по нормали к поверхности равного потенциала; знак «минус» в формуле (3.91) указывает, что потенциальная сила направлена в сторону убывания потенциальной энергии. Надо отметить, что потенциальная энергия была введена дифференциальным путём и поэтому определена с точностью до аддитивной постоянной; эта постоянная будет зафиксирована, если условиться об отсчёте потенциальной энергии от некоторого начального уровня. Желая охарактеризовать работу с точки зрения времени, в течение которого она производится, вводят понятие мощности, как отношения произведенной работы к протекшему времени или как работу, отнесенную к единице времени. Обозначая мощность через N, можем написать:
 эрг/сек = 1 джоуль/сек = 0,102 кГ м/сек,
эрг/сек = 1 джоуль/сек = 0,102 кГ м/сек, 1. Потенциальная энергия силы тяжести вблизи поверхности Земли. В большинстве технических задач можно считать поверхность Земли плоской, а силы тяжести, являющиеся результатом притяжения тел Землей, направленными по вертикали вниз и не изменяющимися в различных точках околоземного пространства. Рассмотрим отдельную тяжелую точку; для нее (ось z направлена по вертикали вверх) и элементарная работа определится выражением:
1. Потенциальная энергия силы тяжести вблизи поверхности Земли. В большинстве технических задач можно считать поверхность Земли плоской, а силы тяжести, являющиеся результатом притяжения тел Землей, направленными по вертикали вниз и не изменяющимися в различных точках околоземного пространства. Рассмотрим отдельную тяжелую точку; для нее (ось z направлена по вертикали вверх) и элементарная работа определится выражением: 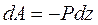 , где Р - сила тяжести (вес) рассматриваемой точки. С другой стороны, по уравнению (3.92), имеем
, где Р - сила тяжести (вес) рассматриваемой точки. С другой стороны, по уравнению (3.92), имеем  . Таким образом, d П = Pdz = d(Pz) и потенциальная энергия силы тяжести представляется формулой П = Pz + С. Для системы N тяжелых точек элементарная работа найдется суммированием отдельных элементарных работ сил тяжести точек системы
. Таким образом, d П = Pdz = d(Pz) и потенциальная энергия силы тяжести представляется формулой П = Pz + С. Для системы N тяжелых точек элементарная работа найдется суммированием отдельных элементарных работ сил тяжести точек системы .
. . Здесь Р - общий вес системы, a
. Здесь Р - общий вес системы, a  - координата ее центра тяжести.
- координата ее центра тяжести.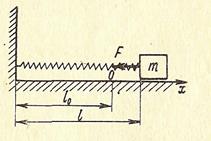
 , один конец которой закреплен неподвижно (рис 62), а к другому подвижному концу прикреплена точка массы
, один конец которой закреплен неподвижно (рис 62), а к другому подвижному концу прикреплена точка массы  ; при растяжении (или сжатии) пружины ее длина будет равна
; при растяжении (или сжатии) пружины ее длина будет равна  , а на массу
, а на массу  . Помещая начало координат на конце недеформированной пружины, направим ось х по движению массы
. Помещая начало координат на конце недеформированной пружины, направим ось х по движению массы  , откуда, интегрируя, получаем
, откуда, интегрируя, получаем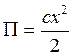 (3.93)
(3.93)
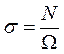 пропорциональны относительному удлинению
пропорциональны относительному удлинению  ; здесь Ω - площадь поперечного сечения,
; здесь Ω - площадь поперечного сечения, 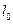 - первоначальная длина стержня. Коэффициентом пропорциональности служит модуль нормальной упругости (модуль Юнга) Е, поэтому
- первоначальная длина стержня. Коэффициентом пропорциональности служит модуль нормальной упругости (модуль Юнга) Е, поэтому  , и, таким образом, упругая сила, с которой деформированный стержень действует на прикрепленную к его концу массу, будет определяться формулой
, и, таким образом, упругая сила, с которой деформированный стержень действует на прикрепленную к его концу массу, будет определяться формулой
 , и коэффициент жесткости с, входящий в выражение (3.93) для потенциальной энергии деформации, в этом случае будет равен
, и коэффициент жесткости с, входящий в выражение (3.93) для потенциальной энергии деформации, в этом случае будет равен 

 , где
, где  - длина пролета, а
- длина пролета, а  - момент инерции поперечного сечения балки. Для консольной балки будем иметь
- момент инерции поперечного сечения балки. Для консольной балки будем иметь 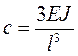 . Формула (3.93) теперь дает потенциальную энергию деформации изгиба балки.
. Формула (3.93) теперь дает потенциальную энергию деформации изгиба балки. , где Mz есть упругий момент, создаваемый касательными напряжениями в поперечном сечении цилиндра; G — модуль сдвига;
, где Mz есть упругий момент, создаваемый касательными напряжениями в поперечном сечении цилиндра; G — модуль сдвига;  -полярный момент инерции сечения. Таким образом, момент внутренних сил, действующих в сечении цилиндра, пропорционален углу поворота сечения
-полярный момент инерции сечения. Таким образом, момент внутренних сил, действующих в сечении цилиндра, пропорционален углу поворота сечения  ; элементарная работа этого момента на угле поворота будет полным дифференциалом:
; элементарная работа этого момента на угле поворота будет полным дифференциалом:
 , аналогичном (3.93), причем жесткость стержня на кручение, как это следует из проделанных вычислений, равна
, аналогичном (3.93), причем жесткость стержня на кручение, как это следует из проделанных вычислений, равна  .
. .
. …….,
…….,  приложены к твердому телу в точках
приложены к твердому телу в точках  …….,
…….,  . Выбирая произвольную точку тела О за полюс и обозначая вектор-радиус
. Выбирая произвольную точку тела О за полюс и обозначая вектор-радиус  -й точки тела
-й точки тела  , получим:
, получим:  , т. е. перемещение
, т. е. перемещение  точки
точки  равно геометрической сумме перемещения полюса
равно геометрической сумме перемещения полюса  и перемещения поворота
и перемещения поворота  вокруг полюса (
вокруг полюса ( - бесконечно малый вектор поворота). Тогда элементарная работа силы
- бесконечно малый вектор поворота). Тогда элементарная работа силы  запишется в форме:
запишется в форме: .
. .
.

 - ее главный момент относительно полюса О, получим
- ее главный момент относительно полюса О, получим (3.92а)
(3.92а) , где
, где 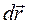 - элементарное перемещение, одинаковое для всех точек тела. При вращении тела вокруг неподвижной оси (пусть это будет ось Oz), выбирая за полюс точку, лежащую на оси вращения, получим
- элементарное перемещение, одинаковое для всех точек тела. При вращении тела вокруг неподвижной оси (пусть это будет ось Oz), выбирая за полюс точку, лежащую на оси вращения, получим  .
.
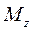 обозначен главный момент системы сил относительно оси Oz, перпендикулярной к плоскости движения и проходящей через полюс О.
обозначен главный момент системы сил относительно оси Oz, перпендикулярной к плоскости движения и проходящей через полюс О.
 - перемещение центра диска,
- перемещение центра диска,  - поворот колеса (здесь по часовой стрелке). Перепишем полученное выражение
- поворот колеса (здесь по часовой стрелке). Перепишем полученное выражение .
. и работа силы трения скольжения равна нулю и
и работа силы трения скольжения равна нулю и 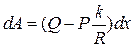 . Если диск катится с проскальзыванием, то
. Если диск катится с проскальзыванием, то  , так как в этом случае
, так как в этом случае  , где f - коэффициент трения скольжения диска о поверхность.
, где f - коэффициент трения скольжения диска о поверхность.
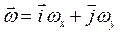 , а тензор инерции
, а тензор инерции 
 представляют функции времени, определяемые интегрированием при заданных начальных условиях дифференциальных уравнений движения, выражающих законы механики. Этой совокупностью функций времени
представляют функции времени, определяемые интегрированием при заданных начальных условиях дифференциальных уравнений движения, выражающих законы механики. Этой совокупностью функций времени  определяется истинное движение системы. Дифференциалы
определяется истинное движение системы. Дифференциалы  обобщенных координат представляют их бесконечно малые изменения в истинном движении, пропорциональные промежутку времени dt:
обобщенных координат представляют их бесконечно малые изменения в истинном движении, пропорциональные промежутку времени dt:  .
.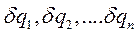 обозначить бесконечно малые приращения обобщенных координат, называемые их вариациями, то упомянутое множество определится совокупностью величин
обозначить бесконечно малые приращения обобщенных координат, называемые их вариациями, то упомянутое множество определится совокупностью величин
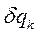 совершенно произвольны. Мы можем сказать, что в момент t связи такой системы, имеющей n степеней свободы, допускают
совершенно произвольны. Мы можем сказать, что в момент t связи такой системы, имеющей n степеней свободы, допускают  конфигураций.
конфигураций. , задаваемую вектор-радиусом
, задаваемую вектор-радиусом 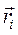 . Изменение
. Изменение  за промежуток времени dt определяется дифференциалом
за промежуток времени dt определяется дифференциалом (4.2)
(4.2) в истинном движении системы. Ему противопоставляется виртуальное или возможное перемещение точки
в истинном движении системы. Ему противопоставляется виртуальное или возможное перемещение точки 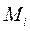 , обозначаемое
, обозначаемое  . Этот бесконечно малый вектор представляет изменение вектор-радиуса точки при мысленном переведении системы из рассматриваемой конфигурации в одну из (
. Этот бесконечно малый вектор представляет изменение вектор-радиуса точки при мысленном переведении системы из рассматриваемой конфигурации в одну из ( ) допускаемых связями бесконечно близких конфигураций; он вычисляется в фиксированный момент t с точностью до первых степеней относительно вариаций
) допускаемых связями бесконечно близких конфигураций; он вычисляется в фиксированный момент t с точностью до первых степеней относительно вариаций  :
: (4.3)
(4.3) связаны теми же соотношениями, что и вариации
связаны теми же соотношениями, что и вариации  ; и истинное перемещение
; и истинное перемещение
 . Дифференциал ее - это приращение функции в процессе движении за промежуток времени dt:
. Дифференциал ее - это приращение функции в процессе движении за промежуток времени dt:

 , отличный от t.
, отличный от t.
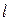 кривой, соединяющей две точки
кривой, соединяющей две точки 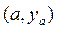 и
и  на плоскости. Как известно, длина кривой на плоскости, заданной функцией у(х), определяется формулой
на плоскости. Как известно, длина кривой на плоскости, заданной функцией у(х), определяется формулой
 в точку
в точку  за кратчайшее время. Оказалось, что линией быстрейшего ската оказалась циклоида.
за кратчайшее время. Оказалось, что линией быстрейшего ската оказалась циклоида. . Для читателя незнакомого с дифференциальным исчислением можно предложить такой способ: взять некоторое значение координаты
. Для читателя незнакомого с дифференциальным исчислением можно предложить такой способ: взять некоторое значение координаты  и сосчитать
и сосчитать  , затем взять
, затем взять  и определить
и определить  . Если
. Если  , то мы на правильном пути. Берём следующее значение
, то мы на правильном пути. Берём следующее значение  и продолжаем наши вычисления до тех пор, пока не достигнем максимума функции. Для читателя, знакомого с дифференциальным исчислением, максимум функции, если он существует, определяется из условия равенства нулю первой производной заданной функции. Совсем иное найти непрерывную функцию у(х), удовлетворяющую граничным условиям
и продолжаем наши вычисления до тех пор, пока не достигнем максимума функции. Для читателя, знакомого с дифференциальным исчислением, максимум функции, если он существует, определяется из условия равенства нулю первой производной заданной функции. Совсем иное найти непрерывную функцию у(х), удовлетворяющую граничным условиям  и
и  , которая сообщает, например, минимум указанного выше функционала. Здесь уже надо рассматривать различные функции, отличающиеся друг от друга. Для читателя незнакомого с вариационным исчислением можно предложить такой способ: взять некоторую функцию
, которая сообщает, например, минимум указанного выше функционала. Здесь уже надо рассматривать различные функции, отличающиеся друг от друга. Для читателя незнакомого с вариационным исчислением можно предложить такой способ: взять некоторую функцию  и сосчитать интеграл
и сосчитать интеграл  . Возьмём новую функцию
. Возьмём новую функцию 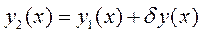 , мало отличающуюся от
, мало отличающуюся от  и снова сосчитаем интеграл
и снова сосчитаем интеграл  . Если
. Если  <
<  , то можно перейти к следующему приближению и т.д. Правда, в этом случае неизвестно, когда надо остановиться. Для читателя, знакомого с вариационным исчислением, минимум функционала, если он существует, определяется из условия равенства нулю первой вариации заданного функционала. Но в отличии от максимума функции, который определятся нахождением одной точки, первая вариация функционала приводит к уравнению Эйлера
, то можно перейти к следующему приближению и т.д. Правда, в этом случае неизвестно, когда надо остановиться. Для читателя, знакомого с вариационным исчислением, минимум функционала, если он существует, определяется из условия равенства нулю первой вариации заданного функционала. Но в отличии от максимума функции, который определятся нахождением одной точки, первая вариация функционала приводит к уравнению Эйлера (4.4)
(4.4) в это уравнение получаем дифференциальное уравнение второго порядка, уравнение экстремалей, решение которого, если оно существует, и
в это уравнение получаем дифференциальное уравнение второго порядка, уравнение экстремалей, решение которого, если оно существует, и 


