
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамики относительного движения точки.Содержание книги
Поиск на нашем сайте
Предположим, что система координат Oxyz может быть принята за абсолютную (неподвижную или галилееву) систему и что в этой системе координат движение точки определяется дифференциальным уравнением
где
где
Подставляя значение ускорения
Введем обозначения:
Вектор Если относительная система
при равномерном вращении (ε = 0) относительной системы вокруг неподвижной или равномерно и поступательно движущейся по отношению к абсолютной системе оси (
Пример 1. Найти условие относительного равновесия тяжелой точки на гладкой кривой данной формы, вращающейся равномерно вокруг вертикальной оси с угловой скоростью ω. Каков должен быть Рис 51 вид кривой для того, чтобы в любом положении на кривой точка была в относительном равновесии (рис. 51) Решение задачи сводится к применению метода кинетостатики. Точка М находится в относи тельном равновесии под влиянием сил: веса G, центробежной силы G cos а — Se sin a = 0, или после подстановки значения Se:
Отрезок rtg а = АВ представляет поднормаль кривой r = f(z), на которой находится точка М, и условие равновесия дается равенством
Подставив Для решения второго вопроса проинтегрируем уравнение (3.13). Найдем уравнение параболы: Пример 2. Относительное равновесие тяжелой точки вблизи поверхности Земли. Найдем условия относительного равновесия груза на нити (отвеса), принимая во внимание вращение Земли. Притяжение F (рис.51а) груза Землей искажается действием центробежной силы Se, так что вес тела, равный натяжению нити N, не будет равен F; кроме того, направление отвеса DM не совпадает с направлением радиуса МО Земли в данном пункте. Обозначим геоцентрическую широту, т. е. угол радиуса Земли с плоскостью земного экватора через λ, а географическую широту, т. е. угол отвесной линии с той же плоскостью, через φ. Уравнение относительного равновесия записываются в виде
проектируя силы на кажущуюся горизонталь НН, получим:
Замечая, что угловая скорость Земли
так что разность
максимальное значение этой разности при φ = 45° будет:
что соответствует приблизительно 6'. Проектируя силы на направление отвеса DM, найдем: N= mg = F cos (φ -λ) — Se cos φ или, вследствие малости угла (φ -λ), Если бы Земля вращалась примерно в 17 раз быстрее, то тела на экваторе не имели бы веса. Переносной силой инерции, вызванной вращением Земли, объясняется также и сжатие Земли. Земля имеет форму геоида, т.е. тела, нормаль к поверхности которого совпадает в каждой точке с линией отвеса. Поверхность геоида можно заменить эллипсоидом вращения, сжатие которого по данным измерений равно Вопросы для самопроверки. 1. Напишите векторную формулу динамики относительного движения точки, что такое силы инерции. 2. Напишите векторную формулу силы сопротивления среды, прокомментируйте введенные обозначения. 3. Напишите в самом общем виде дифференциальные уравнения движения точки (в декартовой системе координат). 4. Напишите дифференциальные уравнения движения точки в осях натурального триэдра.
6. С какой абсолютной скоростью сойдет колечко со стержня, если его длина равна L, начальное положение 7. В чем разница между прямой и обратной (основной) задачами динамики? 8. Напишите уравнение относительного равновесия точки.. 9. Составьте дифференциальное уравнения относительного движения колечка по стержню, вращающемуся с постоянной угловой скоростью ω, трение не учитывать. 10. Чему равно время движения точки на участке горизонтального прямолинейного движения, если начальная скорость 11. Чему равен путь, пройденный точкой, на участке горизонтального прямолинейного движения, если начальная скорость Глава 10.
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 398; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.250 (0.007 с.) |


 обозначает абсолютное ускорение точки. Чтобы составить уравнение движения по отношению к другой системе координат
обозначает абсолютное ускорение точки. Чтобы составить уравнение движения по отношению к другой системе координат  , движущейся заданным образом по отношению к абсолютной системе, вспомним кинематическую зависимость между абсолютным ускорением
, движущейся заданным образом по отношению к абсолютной системе, вспомним кинематическую зависимость между абсолютным ускорением  и относительным ускорением
и относительным ускорением  :
: (3.11)
(3.11)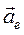 — переносное ускорение, т. е. ускорение того пункта системы
— переносное ускорение, т. е. ускорение того пункта системы  , через который проходит в данный момент рассматриваемая движущая точка,
, через который проходит в данный момент рассматриваемая движущая точка, 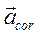 - кориолисово ускорение точки, обусловленное вращательным движением относительной системы
- кориолисово ускорение точки, обусловленное вращательным движением относительной системы  по отношению к абсолютной системе Oxyz (гл 8,§3).
по отношению к абсолютной системе Oxyz (гл 8,§3). ,
, 
 из (3.11) в основное уравнение, получим:
из (3.11) в основное уравнение, получим:

 , и условимся в дальнейшем опускать индекс «
, и условимся в дальнейшем опускать индекс « » у элементов относительного движения; тогда последнее равенство примет вид
» у элементов относительного движения; тогда последнее равенство примет вид (3.12)
(3.12) называется переносной силой инерции, а
называется переносной силой инерции, а  - поворотной или кориолисовой силой инерции. Анализ формулы (3.12) приводит к следующему выводу: дифференциальные уравнения динамики относительного движения составляются так же, как и в абсолютной системе, только к непосредственно приложенным силам присоединяются еще силы инерции — переносная и кориолисова.
- поворотной или кориолисовой силой инерции. Анализ формулы (3.12) приводит к следующему выводу: дифференциальные уравнения динамики относительного движения составляются так же, как и в абсолютной системе, только к непосредственно приложенным силам присоединяются еще силы инерции — переносная и кориолисова. =
= 
 ) получим:
) получим:  , (это центробежная сила). Кориолисова сила не будет входить в формулы относительного движения, если относительная система движется поступательно (
, (это центробежная сила). Кориолисова сила не будет входить в формулы относительного движения, если относительная система движется поступательно (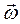 = 0) или если в силу характера связей точка вынуждена двигаться параллельно оси вращения (
= 0) или если в силу характера связей точка вынуждена двигаться параллельно оси вращения ( ). Из уравнения относительного движения легко получить уравнения относительного равновесия. Для этого достаточно в формуле (3.12) положить
). Из уравнения относительного движения легко получить уравнения относительного равновесия. Для этого достаточно в формуле (3.12) положить  =
=  = 0; тогда уравнение относительного равновесия будет:
= 0; тогда уравнение относительного равновесия будет:  =0.
=0. Все, что сейчас говорилось по отношению к точке, может быть перенесено на случай любой системы точек. Прикладывая силы инерции, мы можем рассмотрение движения в относительной системе координат свести к тем же уравнениям, что и в абсолютной.
Все, что сейчас говорилось по отношению к точке, может быть перенесено на случай любой системы точек. Прикладывая силы инерции, мы можем рассмотрение движения в относительной системе координат свести к тем же уравнениям, что и в абсолютной. , где
, где  и реакции кривой
и реакции кривой  которая направлена по нормали
которая направлена по нормали  к кривой. Написав условие равновесия в проекции на касательную, получим:
к кривой. Написав условие равновесия в проекции на касательную, получим:
 . Заменяя
. Заменяя  перепишем условие относительного равновесия в виде
перепишем условие относительного равновесия в виде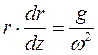 . (3.13)
. (3.13) получим значение ординаты
получим значение ординаты  , в которой при данном
, в которой при данном  будет иметь место равновесие.
будет иметь место равновесие.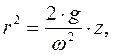 при вращении этой параболы с угловой скоростью
при вращении этой параболы с угловой скоростью  тяжелый шарик будет в любой ее точке находиться в состоянии безразличного относительного равновесия. Как известно, свободная поверхность жидкости в сосуде, приведённом во вращение, принимает форму параболоида.
тяжелый шарик будет в любой ее точке находиться в состоянии безразличного относительного равновесия. Как известно, свободная поверхность жидкости в сосуде, приведённом во вращение, принимает форму параболоида. ,
,
 Заменим здесь Se и F по формулам
Заменим здесь Se и F по формулам 
 , где m — масса груза, R — средний радиус Земли,
, где m — масса груза, R — средний радиус Земли,  - ускорение, вызываемое притяжением Земли; это ускорение не следует смешивать с кажущимся ускорением g, т. е. ускорением
- ускорение, вызываемое притяжением Земли; это ускорение не следует смешивать с кажущимся ускорением g, т. е. ускорением  , искаженным центробежной силой. После замены получим:
, искаженным центробежной силой. После замены получим:
 1/сек, радиус Земли R =6350000 м и ускорение
1/сек, радиус Земли R =6350000 м и ускорение  , получим:
, получим:
 очень мала и предыдущее уравнение можно записать в виде
очень мала и предыдущее уравнение можно записать в виде Рис 51а
Рис 51а
 . Отсюда легко найти относительную разность между
. Отсюда легко найти относительную разность между  и g: Максимальное значение это отношение имеет на экваторе (φ = 0):
и g: Максимальное значение это отношение имеет на экваторе (φ = 0): 
 .
.
 5. Сколько (и какие) необходимо задать начальных условий для определения движения точки (в декартовой системе координат)?
5. Сколько (и какие) необходимо задать начальных условий для определения движения точки (в декартовой системе координат)?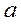 , угловая скорость вращения стержня ω. Стержень перпендикулярен оси вращения.
, угловая скорость вращения стержня ω. Стержень перпендикулярен оси вращения. , а конечная
, а конечная 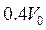 ? Сила сопротивления среды равна
? Сила сопротивления среды равна  .
.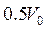 ? Сила сопротивления среды равна
? Сила сопротивления среды равна  .
.


