
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения движения материальной точки.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Проектируя уравнение (1) на координатные оси и учитывая зависимости задаваемых сил от координат, скоростей и времени, получим дифференциальные уравнения динамики точки. Так, для декартовых координат имеем:
Дифференциальные уравнения движения в цилиндрической системе координат будут иметь вид
В заключение приведем дифференциальные уравнения динамики точки в проекциях на оси натурального триэдра; эти уравнения бывают особенно удобны в тех случаях, когда известна траектория движения точки. Проектируя уравнение (3.1) на касательную, главную нормаль и бинормаль к траектории, получаем
Рассмотрим теперь на примере уравнений динамики точки в декартовых координатах (3.2) постановку и процесс решения задач динамики точки. Существуют две основные задачи динамики точки: прямая и обратная. Первая задача динамики (прямая) состоит в следующем: дано движение точки, обладающей массой
требуется найти силы, вызывающие это движение. Решение этой задачи не представляет затруднении. Согласно уравнениям (3.1) и (3.3) находим проекции
Выражения (3.4) представляют проекции равнодействующей всех сил, действующих на точку; часть сил (или часть проекций)могут быть известными, остальные (но не более трёх проекций) найдутся из уравнений (3.4). Эту задачу можноформально привести к решению задачи статики, если переписать уравнение (3.1) в виде
Здесь Вторая (обратная или основная) задача динамики точки ставится следующим образом: на точку массы т, положение и вектор скорости которой в начальный момент времени известны, действуют заданные силы; требуется найти движение этой точки (ее координаты х,у,z) как функции времени. Так как правые части уравнений (3.2) -проекции сил на оси х, у, z- являются известными функциями координат, их первых производных и времени, то для получения требуемого результата надо проинтегрировать систему трех обыкновенных дифференциальных уравнений второго порядка. Аналитическое решение такой задачи оказывается возможным лишь в отдельных частных случаях. Однако численные методы позволяют решить задачу с практически любой необходимой степенью точности. Предположим, что мы проинтегрировали систему дифференциальных уравнений (3.2) и нашли выражения для координат х, у, z в функции времени. Так как система (3.2) имеет шестой порядок, то при интегрировании ее появятся шесть произвольных постоянных и мы получим следующие выражения для координат:
Для определения постоянных
Подставляя в найденное выражение (3.5) первую группу начальных условий (3.6) при t =0, получаем три уравнения, связывающие постоянные интегрирования:
Недостающие три соотношения находятся следующим образом: дифференцируем уравнения движения (3.5) по времени и подставляем в полученные выражения вторую группу начальных условий (3.6) при t = 0; имеем
Решая теперь совместно эти шесть уравнений, получим искомые значения шести произвольных постоянных интегрирования
При составлении дифференциальных уравнений движения точки для конкретного случая следует, прежде всего, оценить действия различных факторов: учесть основные силы и отбросить второстепенные. При решении различных технических задач часто пренебрегают силами сопротивления воздуха и силами сухого трения; так, например, поступают при вычислении собственных частот колебательных систем, на значения которых упомянутые силы оказывают незначительное влияние. Если тело движется вблизи поверхности земли, то его силу тяжести считают постоянной, а поверхности земли — плоской; при удалении от поверхности земли па расстояния, сравнимые с ее радиусом, необходимо уже принимать во внимание изменение силы тяжести с высотой, поэтому в таких задачах используется закон тяготения Ньютона. Нельзя пренебрегать силой сопротивления воздуха при больших скоростях движения тела; в этом случае обычно принимают квадратичный закон сопротивления (сила сопротивления считается пропорциональной квадрату скорости движения тела).
Здесь
Если движение тела происходит в вязкой среде, то и при небольших скоростях движения надо учитывать силу сопротивления, однако в этой задаче достаточно считать ее пропорциональной первой степени скорости. Пример. Рассмотрим задачу о прямолинейном движении точки в среде с сопротивлением, сила сопротивления задана выражением (3.6). Начальная скорость точки -
или
Это дифференциальное уравнение с разделяющимися переменными, решение которого может быть представлено в виде
проинтегрировав левую и правую части, получим следующее решение
Для определения пройденного расстояния перейдём к новым координатам, для этого умножим левую и правую части уравнения (3.7) на
тогда и здесь получаем дифференциальное уравнение с разделяющимися переменными
или Из формул (3.8) и (3.9) получаем выражение для средней скорости
Для Но если положить
Неопределённость вида
Проделав выкладки аналогичные предыдущему решению, получим
Для
Для определения пройденного расстояния переходим к зависимости S(x) и получаем
Для
Тогда средняя скорость равна
Как видно в этом случае время и пройденный путь конечны, а средняя скорость определяется формулой (3.10).
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 609; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.2.6 (0.011 с.) |



 (3.2)
(3.2) ;
;

 ,
,  ,
, 
 , т. е. заданы функции
, т. е. заданы функции (3.3)
(3.3) для чего дважды дифференцируем заданные функции (3.3).
для чего дважды дифференцируем заданные функции (3.3). ,
,  ,
,  (3.4)
(3.4)
 - сила инерции точки, проекции которой на оси х, у, z равны выражениям (3.3) с противоположными знаками. Формальное сведение задачи динамики к задаче статики при помощи введения сил инерции, которое довольно часто практикуется в задачах механики, носит название метода кинетостатики.
- сила инерции точки, проекции которой на оси х, у, z равны выражениям (3.3) с противоположными знаками. Формальное сведение задачи динамики к задаче статики при помощи введения сил инерции, которое довольно часто практикуется в задачах механики, носит название метода кинетостатики.

 (3.5)
(3.5) (i = 1, 2,... 6) в этом решении следует обратиться к начальным условиям задачи. Записывая поставленные условия применительно к декартовым координатам, имеем при t = 0
(i = 1, 2,... 6) в этом решении следует обратиться к начальным условиям задачи. Записывая поставленные условия применительно к декартовым координатам, имеем при t = 0
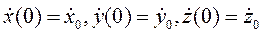 (3.6)
(3.6)

 .
.



 (9)
(9)
 (3.6)
(3.6) - скоростной напор, ρ – плотность среды, в которой движется точка,
- скоростной напор, ρ – плотность среды, в которой движется точка,  - коэффициент сопротивления,
- коэффициент сопротивления, 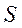 - характерный поперечный размер. Однако, как будет показано ниже, в некоторых задачах необходимо учитывать внутреннее трение в жидкости (в газе), что приводит к более общей формуле для определения силы сопротивления
- характерный поперечный размер. Однако, как будет показано ниже, в некоторых задачах необходимо учитывать внутреннее трение в жидкости (в газе), что приводит к более общей формуле для определения силы сопротивления
 , конечная -
, конечная -  . Надо определить среднюю скорость движения на заданном интервале скоростей. Из формулы (3.2) имеем
. Надо определить среднюю скорость движения на заданном интервале скоростей. Из формулы (3.2) имеем
 (3.7)
(3.7) ,
, (3.8)
(3.8) ; при этом заметим, что
; при этом заметим, что .
. ,
, (3.9)
(3.9) .
. средняя скорость равна
средняя скорость равна  .
. , то нетрудно увидеть, что в этом случае
, то нетрудно увидеть, что в этом случае  и
и  , то есть движущееся тело никогда не остановится, что, во-первых, противоречит здравому смыслу, а во-вторых неясно чему будет равна средняя скорость. Чтобы определить
, то есть движущееся тело никогда не остановится, что, во-первых, противоречит здравому смыслу, а во-вторых неясно чему будет равна средняя скорость. Чтобы определить 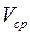 возьмём левые интегралы в пределах от
возьмём левые интегралы в пределах от  и
и 
 .
. раскрыта по правилу Лопиталя. Столь необычный результат является следствием неправильно выбранной модели сопротивления движению. Рассмотрим пример, в котором сила сопротивления задана формулой
раскрыта по правилу Лопиталя. Столь необычный результат является следствием неправильно выбранной модели сопротивления движению. Рассмотрим пример, в котором сила сопротивления задана формулой 
 или
или 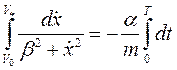 .
. ,
, имеем
имеем .
.

 ,
, (3.10)
(3.10)


