
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Устойчивость равновесия голономной системы в консервативном силовом поле.Содержание книги
Поиск на нашем сайте
Определение понятия устойчивости равновесия связано с рассмотрением тех движений, которые система станет совершать, будучи выведена из положения равновесия путем сообщения ее точкам весьма малых начальных отклонений от положения равновесия и весьма малых начальных скоростей. Если после нарушения равновесия система в своем последующем движении будет весьма мало отклоняться от исследуемого равновесного положения, то такое положение равновесия называется устойчивым. Будем определять положение системы при помощи независимых обобщенных координат
Например, нижнее вертикальное положение маятника устойчиво, наоборот, вертикальное верхнее положение маятника неустойчиво. Лагранж установил следующее достаточное условие устойчивости равновесия голономной системы с идеальными связями в консервативном силовом поле: если в некотором положении системы, подчиненной идеальным, голономным связям и находящейся под действием консервативных сил, потенциальная энергия имеет минимум, то это положение равновесия устойчиво. Точное доказательство этой теоремы дал Лежен-Дирихле. Потенциальная энергия
Принимая во внимание, что в точке (0, 0,..., 0) потенциальная энергия принята равной нулю и что по условию экстремума равны нулю и все ее первые производные в этой точке, будем иметь следующее разложение потенциальной энергии:
Однородный многочлен второй степени (квадратичная форма) будет знакоопределенным, если он сохраняет постоянный знак при вещественных значениях аргументов, обращаясь в нуль только при обращении в нуль всех аргументов. Если же этот многочлен, сохраняя знак, может обращаться в нуль при значениях аргументов, не равных одновременно нулю, то он называется знакопостоянным.
Так, квадратичная форма Известно, что если члены второго порядка, стоящие в разложении (5.1), представляют знакоопределенную положительную квадратичную форму, то функция П при достаточно малых значениях аргументов остается положительной, т. е. имеет в начале координат минимум. Если же эта квадратичная форма знакопостоянна и положительна, то суждение о наличии или отсутствии минимума П не может быть получено из рассмотрения членов второго порядка и требует привлечения членов высших порядков. Теорема Лагранжа — Дирихле содержит утверждение об устойчивости равновесия системы в том ее положении, где потенциальная энергия задаваемых сил достигает минимума, но не дает никаких оснований судить о том, будет ли равновесие неустойчиво, если потенциальная энергия в этом положении системы имеет максимум. Ответ на этот важный вопрос для весьма обширного класса случаев содержится в теоремах Ляпунова. Доказательство теорем Ляпунова не может быть здесь дано; удовольствуемся их формулировкой. Приводим формулировку теорем Ляпунова. Первая теорема Ляпунова. Равновесие неустойчиво, если отсутствие минимума потенциальной энергии узнается по членам второго порядка в разложении потенциальной энергии без необходимости рассматривать члены высших порядков. Вторая теорема Ляпунова. Равновесие неустойчиво, если потенциальная энергия имеет максимум и наличие этого максимума может быть установлено из рассмотрения членов наименее высокого порядка, которые имеются в разложении потенциальной энергии в степенной ряд. В том случае, когда квадратичная форма в разложении (5.1) может принимать как положительные, так и отрицательные значения (является знакопеременной), функция П не имеет в начале координат ни максимума, ни минимума.
|
||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.218.210 (0.007 с.) |

 …..
…..  , число которых равно числу степеней свободы системы. Начальные значения обобщенных координат и скоростей (в момент t = 0) обозначим соответственно через
, число которых равно числу степеней свободы системы. Начальные значения обобщенных координат и скоростей (в момент t = 0) обозначим соответственно через  а их текущие значения (т. е. значения в любой момент времени) через
а их текущие значения (т. е. значения в любой момент времени) через  .(рис 66) Согласно данному выше определению исследуемое равновесное положение устойчиво, если при наперед выбранных положительных, достаточно малых
.(рис 66) Согласно данному выше определению исследуемое равновесное положение устойчиво, если при наперед выбранных положительных, достаточно малых  можно указать такие
можно указать такие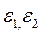 зависящие от, положительные числа
зависящие от, положительные числа  , что при
, что при  и
и  все текущие значения координат
все текущие значения координат 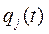 и обобщенных скоростей
и обобщенных скоростей  по абсолютному значению останутся при любом t, как бы велико оно ни было, меньшими, чем
по абсолютному значению останутся при любом t, как бы велико оно ни было, меньшими, чем  и
и  т.е.
т.е.  и
и 
 может быть вблизи положения равновесия системы (пусть
может быть вблизи положения равновесия системы (пусть 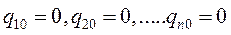 ) разложена в степенной ряд, сходимость которого в области достаточно малых
) разложена в степенной ряд, сходимость которого в области достаточно малых  обеспечена.
обеспечена.
 (5.1)
(5.1) является знакоопределенной, тогда как форма
является знакоопределенной, тогда как форма  будет положительной знакопостоянной, так как она обращается в нуль на прямой
будет положительной знакопостоянной, так как она обращается в нуль на прямой  , а не только в начале координат.
, а не только в начале координат.


