
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вывод уравнения Лагранжа второго рода.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Уравнения Лагранжа второго рода представляют дифференциальные уравнения несвободной системы, составленные в обобщенных координатах. Наибольшее распространение получили уравнения в независимых обобщенных координатах, — их обычно и называют уравнениями Лагранжа второго рода, а иногда просто уравнениями Лагранжа, так как уравнениями Лагранжа первого рода пользуются сравнительно редко. Рассмотрим систему с n степенями свободы, подчиненную идеальным голономным связям. Положение системы в пространстве будем определять n независимыми обобщенными координатами
Так как все обобщённые координаты считаем независимыми, то все
Производные обобщенных координат по времени, т. е. величины
Это первое тождество Лагранжа. Докажем второе тождество
Для этого, дифференцируя обе части (4.19) по
С другой стороны, составим непосредственно
Сравнивая последние два равенства, убеждаемся в справедливости соотношения (4.21). Обратимся к общему уравнению динамики (4.18) и перепишем его в виде
Первая сумма уже была выражена через обобщенные координаты (4.11); она равна
скалярное произведение под знаком суммы преобразуется к виду
или по формулам (4.20) и (4.21)):
Подставляя последнее выражение в круглую скобку правой части равенства (4.23) и замечая, что сумма
Уравнение (4.18) теперь перепишется так:
Последнее равенство может выполняться при произвольных
Уравнения (4.25) представляют совокупность n (по числу степеней свободы) обыкновенных дифференциальных уравнений второго порядка с n независимыми обобщенными координатами, являющимися искомыми функциями времени. Оператор
носит название оператор Эйлера-Лагранжа. Уравнению Лагранжа второго рода можно дать и другое доказательство. Как указывалось выше, положение любой точки можно представить в виде
(при этом
Справа в выражении (4.27) стоит по (4.11) обобщённая сила, а слева выражение (4.23). Проведя аналогичные преобразования, получаем уравнение Лагранжа второго рода.
Пример. Рассмотрим задачу о колебаниях стержня массы m и длины l, подвешенного в точке D к вращающемуся вокруг вертикальной оси АВ стержню АВD. Момент инерции стержня АВD равен J. За обобщённые координаты выберем углы
Здесь
Проведя несложные преобразования, запишем кинетическую энергию в виде
Совсем нетрудно получить и выражение для возможной работы сил--момента
Обобщённые силы будут
Второе уравнение будет
Диссипативная функция.
К числу диссипативных сил относятся силы сопротивления движению точек системы, направленные противоположно их скоростям. Мы рассмотрим случай сил сопротивления, представимых в виде
где
Заметив, что
находим
где через Ф обозначена величина, называемая диссипативной функцией
Заметим, что Ф>0, так как подынтегральные функции положительны. Диссипативная функция была введена в классическом труде Релея «Теория звука» для сил сопротивления, пропорциональных первой степени скорости. Здесь это понятие обобщено на силы более общего вида. В случае одночленной степенной зависимости сил сопротивления от скорости
будет однородной функцией (m+1) степени от обобщенных скоростей, которую легко выразить через мощность диссипативных сил
Здесь применена теорема Эйлера об однородных функциях. Отметим, что m = 0 соответствует кулонову (сухому) трению, m=1 —силам вязкого трения, пропорциональным первой степени скорости (случай Релея), m = 2 — силам квадратичного сопротивления. При составлении обобщенных сил по формуле (4.29) необходимо иметь в виду, что дифференцируются выражения, содержащие модуль обобщенных скоростей. Например, при сопротивлении, пропорциональном четной степени скорости и n =1 (одна степень свободы)
где
|
||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 669; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.105.195 (0.011 с.) |

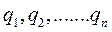 . Вектор-радиус
. Вектор-радиус  любой точки системы может быть выражен через обобщенные координаты и время
любой точки системы может быть выражен через обобщенные координаты и время  , а возможные перемещения определятся как вариации вектор-радиусов;
, а возможные перемещения определятся как вариации вектор-радиусов;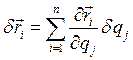 .
.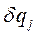 представляют произвольные бесконечно малые величины. Докажем предварительно два тождества Лагранжа. Составим выражения векторов скоростей точек системы:
представляют произвольные бесконечно малые величины. Докажем предварительно два тождества Лагранжа. Составим выражения векторов скоростей точек системы: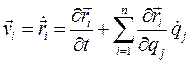 (4.19)
(4.19)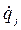 называются обобщенными скоростями. Формулы (4.19) показывают, что скорость
называются обобщенными скоростями. Формулы (4.19) показывают, что скорость 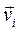 любой точки линейно выражается через обобщенные скорости, Поэтому, обозначая через к произвольный индекс, изменяющийся от 1 до n, будем иметь:
любой точки линейно выражается через обобщенные скорости, Поэтому, обозначая через к произвольный индекс, изменяющийся от 1 до n, будем иметь: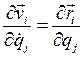 (4.20)
(4.20)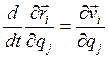 (4.21)
(4.21) , получим
, получим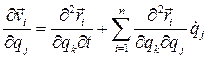

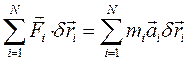 (4.22)
(4.22)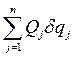 , где Qj — обобщенная сила. Что касается второй суммы в уравнении (4.22), то ее можно преобразовать, пользуясь (4.9) и меняя порядок суммирования:
, где Qj — обобщенная сила. Что касается второй суммы в уравнении (4.22), то ее можно преобразовать, пользуясь (4.9) и меняя порядок суммирования: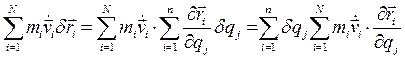 (4.23)
(4.23)
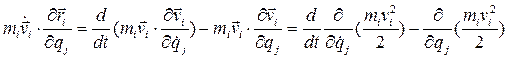
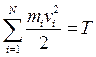 определяет кинетическую энергию системы, получим:
определяет кинетическую энергию системы, получим: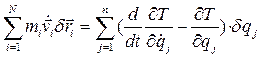
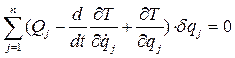 (4.24)
(4.24) , только если все круглые скобки равны нулю. Таким образом, мы приходим к уравнениям Лагранжа второго рода, составленным в независимых обобщенных координатах для системы с голономными связями:
, только если все круглые скобки равны нулю. Таким образом, мы приходим к уравнениям Лагранжа второго рода, составленным в независимых обобщенных координатах для системы с голономными связями: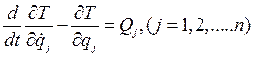 (4.25)
(4.25) (4.26)
(4.26) , где n - число независимых обобщённых координат, равное, в нашем случае, числу степеней свободы системы. Тогда
, где n - число независимых обобщённых координат, равное, в нашем случае, числу степеней свободы системы. Тогда 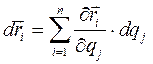 и величину
и величину 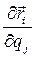 можно представить как направление вдоль координатной линии
можно представить как направление вдоль координатной линии  . Спроектируем основное уравнение динамики точки на это направление
. Спроектируем основное уравнение динамики точки на это направление
 есть сумма всех сил: внешних и внутренних, действующих на точку) и сложим все полученные проекции.
есть сумма всех сил: внешних и внутренних, действующих на точку) и сложим все полученные проекции.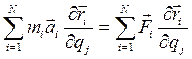 (4.27)
(4.27)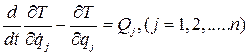 .
. и φ. Кинетическая энергия системы в общем виде запишется в форме
и φ. Кинетическая энергия системы в общем виде запишется в форме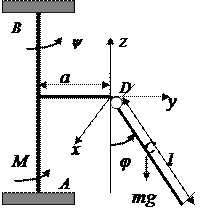
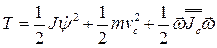 ,
,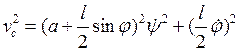 - скорость центра стержня,
- скорость центра стержня, 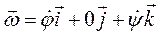 - вектор угловой скорости стержня,
- вектор угловой скорости стержня,  -тензор инерции стержня относительно центра С. Подставив введённые обозначения в формулу для кинетической энергии, получим
-тензор инерции стержня относительно центра С. Подставив введённые обозначения в формулу для кинетической энергии, получим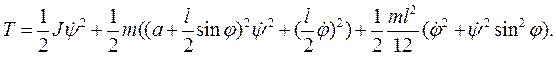
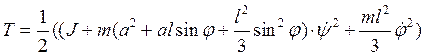
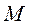 и силы тяжести
и силы тяжести 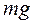 .
. .
.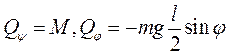 . Составим уравнения движения с помощью уравнения Лагранжа второго рода:
. Составим уравнения движения с помощью уравнения Лагранжа второго рода: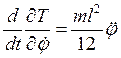 ; обозначим
; обозначим 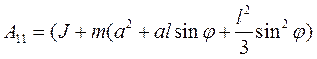 , и
, и  , тогда
, тогда 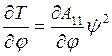 и первое уравнение имеет вид
и первое уравнение имеет вид .
.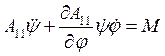 .
.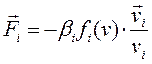 , (4.28)
, (4.28) — величина скорости точки
— величина скорости точки  ;
;  и
и 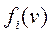 — положительные функции от обобщенных координат и соответственно от скоростей
— положительные функции от обобщенных координат и соответственно от скоростей 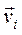 . По (4.10) и (4.20) (первое тождество Лагранжа) соответствующие этим силам обобщенные силы определяются равенствами
. По (4.10) и (4.20) (первое тождество Лагранжа) соответствующие этим силам обобщенные силы определяются равенствами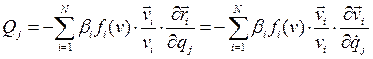 ,
,  .
.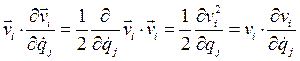 ,
,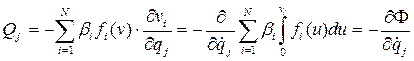 (4.29)
(4.29) (4.30)
(4.30)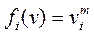 диссипативная функция
диссипативная функция (4.31)
(4.31) (4.32)
(4.32)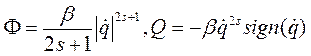 (4.33)
(4.33)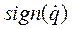 означает знак функции φ (
означает знак функции φ (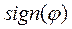 )= 1, если φ > 0 и
)= 1, если φ > 0 и  =-1, если φ < 0).
=-1, если φ < 0).


