
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные уравнения с постоянными коэффициентамиСодержание книги
Поиск на нашем сайте
Дифференциальное уравнение вида
где Если f - непрерывная функция, то общее решение уравнения (1) состоит из суммы общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения (1). Чтобы решить однородное линейное уравнение с постоянными коэффициентами (1) надо составить характеристическое уравнение
и найти его корни
где Если все коэффициенты однородного уравнения (1) вещественные, то решение можно написать в вещественной форме и в случае комплексных корней
если эти корни простые, и слагаемые
если каждый из корней Пример 1. Решить уравнение Решение. Выпишем характеристическое уравнение, соответствующее данному однородному уравнению
Разлагая левую часть уравнения на множители, находим корни:
Следуя выше изложенной теории, выпишем общее решение данного уравнения
Для линейных неоднородных уравнений с постоянными коэффициентами и с правой частью специального вида, а именно состоящей из сумм и произведений функций
Здесь Теорема (принцип суперпозиции). Пусть
соответственно. Тогда
есть решение уравнения
Пример 2. Решить уравнение Решение. Сначала найдем общее решение данного неоднородного уравнения второго порядка, а затем среди всех решений выберем то, которое удовлетворяет заданным условиям. Так как характеристическое уравнение
Правая часть исходного неоднородного уравнения представляет собой сумму двух функций специального вида
соответственно. Определим частное решение
где коэффициенты a и b подлежат определению. Подставляя последнее выражение в (*), и приравнивая коэффициенты при одинаковых степенях x в левой и правой частях, получим следующую систему:
откуда
Правая
Подставляя
Откуда
а его общее решение определяется функцией:
Чтобы решить задачу Коши, определим значения произвольных постоянных
откуда
Линейное неоднородное уравнение (1) с любой правой частью
Функции
Пример 3. Решить уравнение Решение. Исходное уравнение есть линейное неоднородное уравнение второго порядка. Решим соответствующее однородное уравнение
Функции
Решая систему, находим
Тогда функция
определяет общее решение исходного уравнения.
Рассмотрим дифференциальные уравнения, сводящиеся к линейным уравнения с постоянными коэффициентами. 1. Уравнение Эйлера. Это уравнение вида
где
Пример 4. Решить уравнение Решение. Решение будем искать в виде
решая которое, находим
2. Уравнение Лагранжа. Это уравнение вида
где Пример 5. Решить уравнение Решение. Решение будем искать в виде
решая которое, находим
3. Уравнение Чебышева. Это уравнение вида
Заменой
Пример 6. Решить уравнение Решение. Заменой
Решая которое, и переходя к старым переменным получаем общее решение данного уравнения
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 284; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.34.211 (0.008 с.) |

 (1)
(1) , f - известная функция, называется линейным дифференциальным уравнением n - го порядка с постоянными коэффициентами. Если
, f - известная функция, называется линейным дифференциальным уравнением n - го порядка с постоянными коэффициентами. Если  , то уравнение (1) называется однородным, в противном случае - неоднородным. К однородному уравнению, очевидно, применима теорема существования и единственности, причем интервалом определения решений этого уравнения будет вся действительная ось.
, то уравнение (1) называется однородным, в противном случае - неоднородным. К однородному уравнению, очевидно, применима теорема существования и единственности, причем интервалом определения решений этого уравнения будет вся действительная ось. (2)
(2) . Каждому простому корню
. Каждому простому корню  соответствует частое решение однородного уравнения (1), имеющее вид
соответствует частое решение однородного уравнения (1), имеющее вид  , а каждому корню
, а каждому корню  кратности k - решения
кратности k - решения  . Произвольная линейная комбинация всех частных решений является общим решением однородного уравнения (1), т.е.
. Произвольная линейная комбинация всех частных решений является общим решением однородного уравнения (1), т.е. ,
, произвольные постоянные.
произвольные постоянные. . Для каждой пары комплексно сопряженных корней
. Для каждой пары комплексно сопряженных корней  в формулу общего решения включаются слагаемые
в формулу общего решения включаются слагаемые ,
, ,
, имеет кратность k. Здесь
имеет кратность k. Здесь  - многочлены степени k-1.
- многочлены степени k-1. .
. .
. ,
, .
.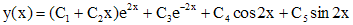 .
. , частное решение можно искать методом неопределенных коэффициентов. Вид частного решения зависит от корней характеристического уравнения. Ниже представлена таблица видов частных решений линейного неоднородного уравнения с правой частью специального вида.
, частное решение можно искать методом неопределенных коэффициентов. Вид частного решения зависит от корней характеристического уравнения. Ниже представлена таблица видов частных решений линейного неоднородного уравнения с правой частью специального вида.



 - не корень
- не корень


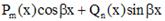
 - не корень
- не корень




 - не корень
- не корень


 -многочлены степени s, а
-многочлены степени s, а  - многочлены степени s, коэффициенты которых нужно найти методом неопределенных коэффициентов. Для того чтобы их найти, нужно функцию, задающую вид частного решения, подставить в исходное дифференциальное уравнение и после приведения подобных слагаемых приравнять соответствующие коэффициенты в правой и левой частях уравнения. В случае, когда для определения вида частного решения нельзя воспользоваться только одной строкой таблицы, применяют принцип суперпозиции.
- многочлены степени s, коэффициенты которых нужно найти методом неопределенных коэффициентов. Для того чтобы их найти, нужно функцию, задающую вид частного решения, подставить в исходное дифференциальное уравнение и после приведения подобных слагаемых приравнять соответствующие коэффициенты в правой и левой частях уравнения. В случае, когда для определения вида частного решения нельзя воспользоваться только одной строкой таблицы, применяют принцип суперпозиции. - решения уравнений
- решения уравнений ,
,
 .
. , удовлетворяющее условиям
, удовлетворяющее условиям  .
. имеет корни
имеет корни  , то общим решением соответствующего однородного уравнения является функция:
, то общим решением соответствующего однородного уравнения является функция: .
. . Найдем методом неопределенных коэффициентов частные решения
. Найдем методом неопределенных коэффициентов частные решения  уравнений
уравнений (*)
(*) (**)
(**) уравнения (*). Правая часть
уравнения (*). Правая часть  представляет собой произведение многочлена первой степени и
представляет собой произведение многочлена первой степени и  . Число, которое нужно сравнивать с корнем характеристического уравнения - это 1. Оно является простым корнем характеристического уравнения кратности 1. Согласуя с параметрами таблицы, имеем
. Число, которое нужно сравнивать с корнем характеристического уравнения - это 1. Оно является простым корнем характеристического уравнения кратности 1. Согласуя с параметрами таблицы, имеем  , следовательно, частное решение будем искать в виде:
, следовательно, частное решение будем искать в виде: ,
,
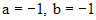 , а значит
, а значит .
. часть уравнения (**) представляет собой произведение многочлена нулевой степени и тригонометрической функции. Число 2i не является корнем характеристического уравнения. Частное решение
часть уравнения (**) представляет собой произведение многочлена нулевой степени и тригонометрической функции. Число 2i не является корнем характеристического уравнения. Частное решение  уравнения (**) ищем в виде (
уравнения (**) ищем в виде ( ):
): .
.
 . Поэтому
. Поэтому  . Согласно принципу суперпозиции, частное решение
. Согласно принципу суперпозиции, частное решение  первоначального уравнения имеет вид:
первоначального уравнения имеет вид: ,
, .
. в общем решении. Для этого в решение и его производную подставим x=0. Используя начальные условия
в общем решении. Для этого в решение и его производную подставим x=0. Используя начальные условия 
 . Значит решение поставленной задачи Коши есть
. Значит решение поставленной задачи Коши есть .
. можно решить методом вариации постоянных. Пусть найдено общее решение
можно решить методом вариации постоянных. Пусть найдено общее решение  соответствующего линейного однородного уравнения. Тогда решения уравнения (1) ищется в виде
соответствующего линейного однородного уравнения. Тогда решения уравнения (1) ищется в виде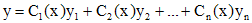 .
.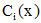 определяются из системы
определяются из системы
 .
. . Характеристическое уравнение для данного однородного уравнения есть
. Характеристическое уравнение для данного однородного уравнения есть  , решениями которого являются
, решениями которого являются  . Тогда общим решением однородного уравнения будет функция
. Тогда общим решением однородного уравнения будет функция  . Тогда решение заданного уравнения будем искать в виде
. Тогда решение заданного уравнения будем искать в виде .
.
 .
.
 ,
, . Заменой
. Заменой  (при
(при  ) уравнение сводится к линейному уравнению с постоянными коэффициентами. На практике решение уравнения Эйлера ищут в виде
) уравнение сводится к линейному уравнению с постоянными коэффициентами. На практике решение уравнения Эйлера ищут в виде  . Для нахождения r получают характеристическое уравнение. Простому корню
. Для нахождения r получают характеристическое уравнение. Простому корню  характеристического уравнения соответствует решение
характеристического уравнения соответствует решение  , а m - кратному корню
, а m - кратному корню  . Если коэффициенты уравнения действительны, а характеристическое уравнение имеет комплексно сопряженные корни
. Если коэффициенты уравнения действительны, а характеристическое уравнение имеет комплексно сопряженные корни  кратности
кратности  , то уравнение Эйлера имеет
, то уравнение Эйлера имеет  линейно независимых решений вида
линейно независимых решений вида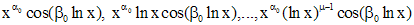 ,
, .
. .
. , для нахождения r получаем характеристическое уравнение
, для нахождения r получаем характеристическое уравнение ,
, . В итоге получаем общее решение исходного уравнения
. В итоге получаем общее решение исходного уравнения .
. ,
, . Заменой
. Заменой  уравнение Лагранжа сводится к линейному уравнению с постоянными коэффициентами.
уравнение Лагранжа сводится к линейному уравнению с постоянными коэффициентами. .
. , для нахождения r получаем характеристическое уравнение
, для нахождения r получаем характеристическое уравнение ,
, . В итоге получаем общее решение исходного уравнения
. В итоге получаем общее решение исходного уравнения .
. .
. (при
(при  ) уравнение Чебышева сводится к уравнению
) уравнение Чебышева сводится к уравнению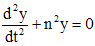 .
. .
. .
. .
.


