
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод интегрирующего множителя.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Умножим обе части уравнение (1) на функцию
Интегрируя последнее уравнение, получим
где Общее определение интегрирующего множителя вместе с некоторыми методами интегрирования, основанными на этом понятии имеется, например, в учебниках[1,3]. Пример 3. Решить задачу Коши Решение. Перепишем уравнение в нормальной форме
Для полученного уравнения интегрирующий множитель ищем в виде
следовательно,
интегрируя последнее уравнение находим
В итоге получаем ответ Иногда уравнение можно сделать линейным, поменяв местами функцию y и независимое переменное x. Затем решать любым выше изложенным способом относительно x. Пример 4. Решить уравнение Данное уравнение является линейным относительно функции x=x(y), т.е.
Общим решением однородного уравнения
Полагая C=C(y) и подставляя в неоднородное уравнение, для функции C(y) получаем дифференциальное уравнение
следовательно,
где
Некоторые дифференциальные уравнения могут быть сведены к линейным путем замены переменных. К таким уравнениям относятся: a) уравнение Бернулли Уравнение вида
называется уравнением Бернулли. Пусть функции
Линейное уравнение имеет вид
Уравнение Бернулли также можно решать другим способом, а именно, сделав замену в уравнении (6)
находим
Возьмем в качестве
Для определения
Пример 5. Решить уравнение Решение. Разделим данное уравнение на
сделаем замену
тогда
Решая, полученное уравнение одним из выше изложенным способом, находим решение исходного уравнения
где Решим уравнение
Функция Положим, например,
откуда,
Перейдя к старым переменным, получаем решением исходного уравнения являются функции
b) уравнение Риккати Уравнение вида
называется уравнением Риккати. Уравнение Риккати интегрируются в квадратурах лишь в некоторых частных случаях - например, если
оно сводится к уравнению Бернулли. Частное решение удобно подбирать по виду функции с(x). Пример 6. Решить уравнение Решение. Преобразуем уравнение к виду
Найдем частное решение методом неопределенных коэффициентов, исходя из вида правой части предположим, что функция
удовлетворяет уравнению Риккати. Тогда должно выполняться равенство
которое возможно при
является частным решением уравнения Риккати. Чтобы найти общее решение сделаем замену
Подставляя в исходное уравнение, получаем уравнение Бернулли с показателем n=2:
Далее, полагая
приводим уравнение Бернулли к линейному неоднородному уравнению
решением которого является функция
Перейдя к старым переменным, находим
При делении на z было потеряно решение
Итак, решением исходного уравнения являются функции
Уравнения в полных дифференциалах. Интегрирующий множитель. Уравнение
называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции
Теорема. Если функции
является необходимым и достаточным для того, чтобы выражение
было полным дифференциалом функции Если известна функция, полным дифференциалом которой является левая часть уравнения (1), то все решения этого уравнения имеют вид Чтобы найти функцию
Интегрируя первое из этих равенств по x, определим функцию
где
Пример 1. Решить уравнение Решение. Так как
во всех точках полуплоскости
Проинтегрировав первое равенство из (4) по x, получим:
Для нахождения
Тогда Решение данного уравнения запишется в виде:
Для интегрирования уравнений вида (1) иногда применяют метод, состоящий в выделении полных дифференциалов из разных групп слагаемых, стоящих в левой части уравнения. Для выделения полных дифференциалов используют формулы:
Пример 2. Решить уравнение Решение. Заметим, что в правой части уравнения стоит функция, зависящая от частного
Обозначим
Разделяя переменные, будем иметь:
Проинтегрировав, ответ запишем в виде:
Конечно, не всякое дифференциальное уравнение вида (1) является уравнением в полных дифференциалах. Всегда можно привести его к уравнению такого типа умножением на некоторую не равную нулю функцию Если
является уравнением в полных дифференциалах:
т.е. интегрирующий множитель есть решение уравнения
Найти функцию Случай 1. Если уравнение (1) имеет интегрирующий множитель, зависящий только от x, т.е.
Случай 2. Если уравнение (1) допускает интегрирующий множитель как функцию одной переменной y, т.е.
Случай 3. Если уравнение (1) имеет интегрирующий множитель вида
Пример 3. Решить уравнение Решение. Очевидно, что данное уравнение не является уравнением в полных дифференциалах. Попытаемся найти интегрирующий множитель
не зависит от y, то уравнение для определения
Данное уравнение является уравнением с разделяющимися переменными одним из решением которого, является функция
Интегрируя его, находим общее решение:
Пример 4. Решить уравнение Решение. Очевидно, найти интегрирующий множитель, зависящий только от одной переменной нельзя. Будем искать интегрирующий множитель в виде
интегрируя, которое находим
Умножая обе части исходного уравнения на данный интегрирующий множитель, получаем уравнение в полных дифференциалах:
Интегрируя полученное уравнение, находим общее решение:
Теорема. Если
Тогда Это свойство интегрирующего множителя позволяет во многих случаях находить его методом разбиения данного уравнения на две части. Пусть
Тогда, в силу приведенной выше теоремы, функции
являются интегрирующими множителями для первого и второго уравнения соответственно. Если удастся подобрать функции
то интегрирующим множителем для уравнения
очевидно, является функция
Пример 5. Решить уравнение Решение. Для отыскания интегрирующего множителя воспользуемся методом разделения уравнения на два:
Нетрудно установить, что интегрирующие множители этих уравнений. а также их интегралы имеют вид:
Согласно указанному методу, интегрирующий множитель данного уравнения ищем из соотношения
Отсюда
Полагая здесь
или
Пусть
Следовательно,
Заметим, что для
В обоих случаях после интегрирования уравнения в полных дифференциалах и упрощений получаем ответ
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 1354; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.92.165 (0.01 с.) |

 , где
, где  определяется по формуле (4). Учитывая, что
определяется по формуле (4). Учитывая, что 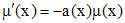 , уравнение (1) перепишется в виде
, уравнение (1) перепишется в виде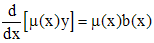 .
. ,
, - произвольная постоянная.
- произвольная постоянная. ,
,  .
.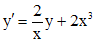 . (5)
. (5) ,
, . Умножив уравнение (5) на
. Умножив уравнение (5) на 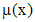 , получим
, получим ,
, .
.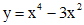 .
. .
. .
. является функция
является функция .
. ,
, ,
, - постоянная интегрирования. Итак, решением исходного неоднородного уравнения является функция
- постоянная интегрирования. Итак, решением исходного неоднородного уравнения является функция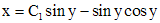 .
. (6)
(6) определены на интервале
определены на интервале  . При
. При 
 всегда является решением. Для ненулевых решений уравнение Бернулли сводится к линейному заменой
всегда является решением. Для ненулевых решений уравнение Бернулли сводится к линейному заменой .
.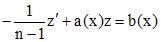 .
. ,
,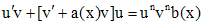 .
. какое-нибудь решение уравнения
какое-нибудь решение уравнения .
. тогда получим уравнение с разделяющимися переменными
тогда получим уравнение с разделяющимися переменными .
. .
. , получим
, получим ,
, ,
, .
. ,
, .
. .
. . Уравнение для определения функции
. Уравнение для определения функции  ,
,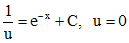 .
.
 - постоянны, то переменные разделяются; при с=0 получается уравнение Бернулли. Если удается угадать некоторое частное решение
- постоянны, то переменные разделяются; при с=0 получается уравнение Бернулли. Если удается угадать некоторое частное решение  уравнение Риккати, то заменой
уравнение Риккати, то заменой
 .
.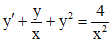 .
.
 ,
, . Следовательно, функция
. Следовательно, функция
 .
. .
.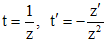 ,
, ,
, .
. .
. .
. (1)
(1) , т.е.
, т.е. .
. непрерывны в некоторой односвязной области
непрерывны в некоторой односвязной области 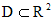 , то условие
, то условие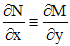

 , где
, где  . (2)
. (2) , (3)
, (3) - произвольная дифференцируемая функция. Функция
- произвольная дифференцируемая функция. Функция  , такая что
, такая что  . Дифференцируя (3) по y, с учетом второго равенства из (2) получаем уравнение для определения
. Дифференцируя (3) по y, с учетом второго равенства из (2) получаем уравнение для определения  .
. .
.
 , то данное уравнение является уравнением в полных дифференциалах. Найдем функцию
, то данное уравнение является уравнением в полных дифференциалах. Найдем функцию  . (4)
. (4) .
. .
.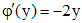 откуда,
откуда,  . Значит
. Значит  .
. .
.
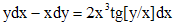 .
.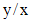 , а в левой - выражение, похожее на дифференциал частного. Поэтому, разделив обе части данного уравнения на
, а в левой - выражение, похожее на дифференциал частного. Поэтому, разделив обе части данного уравнения на  , получим:
, получим: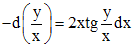 .
. . Тогда полученное уравнение можно записать в виде:
. Тогда полученное уравнение можно записать в виде: .
. .
. .
. , называемую интегрирующим множителем. Но не всегда легко найти такую функцию.
, называемую интегрирующим множителем. Но не всегда легко найти такую функцию.
 ,
, . (5)
. (5)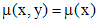 , то из (5) имеем
, то из (5) имеем .
. , то
, то .
.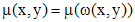 , где
, где 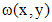 - известная функция, то
- известная функция, то .
. .
.
 примет вид
примет вид .
. . Умножая обе части исходного уравнения на интегрирующий множитель
. Умножая обе части исходного уравнения на интегрирующий множитель  .
. .
. .
. , тогда уравнение для нахождения
, тогда уравнение для нахождения  ,
,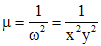 .
. .
. .
. - интегрирующий множитель уравнения вида (1), а функция
- интегрирующий множитель уравнения вида (1), а функция  такая, что
такая, что .
.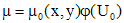 , где
, где  - произвольная дифференцируемая функция, также будет интегрирующим множителем того же уравнения.
- произвольная дифференцируемая функция, также будет интегрирующим множителем того же уравнения. - общие интегралы и интегрирующие множители соответственно для уравнений
- общие интегралы и интегрирующие множители соответственно для уравнений .
.
 так, чтобы выполнялось равенство
так, чтобы выполнялось равенство ,
, ,
, .
. .
. ,
, .
. .
.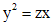 , получаем
, получаем ,
,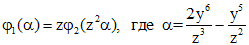 .
. . Тогда
. Тогда .
. .
.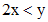 аналогично можно найти
аналогично можно найти .
. .
.


