
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные уравнения с переменными коэффициентамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Линейным дифференциальным уравнением n - го порядка с переменными коэффициентами называется уравнение вида
где Функции
Если тождество (2) справедливо лишь при Пример 1. Решить уравнение Решение. С помощью замены
Общее решение его имеет вид
Пример 2. Исследовать на линейную независимость функции Решение. Согласно определению линейной независимости функций должны найтись такие числа
Отсюда (если эти тождества выполняются) следуют равенства
или Пусть
Если (n-1) раз дифференцируемые функции Если линейно независимые функции
где Общее решение уравнения (3) при
линейно независимых частных решений Пример 3. Могут ли графики двух решений уравнения
с непрерывными коэффициентами на плоскости xOy пересекаться. Решение. Пусть Если n=1, то, в силу единственности задачи Коши имеется только тривиальное решение
в который Совокупность n линейно независимых частных решений линейного однородного уравнения n-го порядка называется его фундаментальной системой. Фундаментальная система решений вполне определяет линейное однородное уравнение (3). Такое уравнение имеет вид
Пример 4. Составить линейное однородное дифференциальное уравнение (возможно меньшего порядка), имеющее частные решения Решение. Очевидно, что функции
Чтобы найти общее решение линейного однородного уравнения второго порядка
где Пример 5. Решить уравнение Решение. По формуле Остроградского - Лиувилля получим
Так как функция
Так как
В итоге получаем общее решение уравнения
Общего метода для отыскания частного решения линейного уравнения второго порядка с переменными коэффициентами не существует. В некоторых случаях решение удается найти путем подбора. Если коэффициенты уравнения являются многочленами, то его частное решение можно найти также в виде многочленов. Пример 6. Найти частное решение уравнения Решение. Сначала найдем степень многочлена. Подставляя
Приравнивая нулю коэффициент при старшей степени x, получим:
Отсюда
Отсюда
|
|||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 2643; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.19.247 (0.007 с.) |

 , (1)
, (1) - известные функции. Если
- известные функции. Если  - частное решение уравнения (1) при
- частное решение уравнения (1) при  , то посредством замены
, то посредством замены  порядок уравнения (1) при
порядок уравнения (1) при 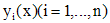 называются линейно зависимыми на сегмента [a,b], если существуют такие постоянные
называются линейно зависимыми на сегмента [a,b], если существуют такие постоянные  , одновременно не равные нулю, что на [a,b] выполняется тождество
, одновременно не равные нулю, что на [a,b] выполняется тождество . (2)
. (2) , то указанные функции называются линейно независимыми на сегменте [a,b].
, то указанные функции называются линейно независимыми на сегменте [a,b]. .
. понижаем порядок данного уравнения:
понижаем порядок данного уравнения: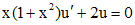 .
. . Интегрируя уравнение
. Интегрируя уравнение 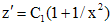 окончательно находим
окончательно находим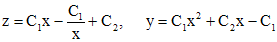 .
. , в области, где они определены.
, в области, где они определены. , одновременно не равные нулю, что выполняется тождество относительно x:
, одновременно не равные нулю, что выполняется тождество относительно x: .
. ,
,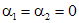 . Следовательно, функции
. Следовательно, функции  линейно независимы.
линейно независимы. - произвольная система функций, заданных на [a,b], определителем Вронского для данной системы является определитель
- произвольная система функций, заданных на [a,b], определителем Вронского для данной системы является определитель .
. линейно зависимы на сегменте [a,b], то
линейно зависимы на сегменте [a,b], то  на [a,b].
на [a,b]. , (3)
, (3) непрерывные на сегменте [a,b] функции, то
непрерывные на сегменте [a,b] функции, то  на [a,b].
на [a,b].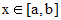 есть линейная комбинация
есть линейная комбинация
 этого уравнения.
этого уравнения. также есть решение этого уравнения, причем
также есть решение этого уравнения, причем  , где
, где  абсцисса точки пересечения графиков решений
абсцисса точки пересечения графиков решений  . Следовательно, двух различных решений нет. Пусть n=2, тогда имеем задачу
. Следовательно, двух различных решений нет. Пусть n=2, тогда имеем задачу
 произвольное, поскольку не задано. Следовательно, графики двух решений задачи могут пересекаться при
произвольное, поскольку не задано. Следовательно, графики двух решений задачи могут пересекаться при  . Аналогичная ситуация и при
. Аналогичная ситуация и при 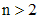 .
. . (4)
. (4)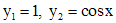 .
. .
. , у которого известно одно частное решение
, у которого известно одно частное решение  ,
, .
. . Разделив обе части уравнения на
. Разделив обе части уравнения на 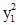 , получим
, получим .
. , то
, то ,
,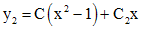 .
. , являющееся алгебраическим многочленом.
, являющееся алгебраическим многочленом. в уравнение и выписывая только члены с самой старшей степенью x, получим:
в уравнение и выписывая только члены с самой старшей степенью x, получим: .
. .
. . Итак, многочлен может быть только второй степени. Ищем его в виде
. Итак, многочлен может быть только второй степени. Ищем его в виде  . Подставляя в исходное уравнение получим
. Подставляя в исходное уравнение получим  , следовательно,
, следовательно,
 . Итак, многочлен
. Итак, многочлен  является частным решением.
является частным решением.


