
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матричный метод решения систем линейных уравненийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ Государственное образовательное учреждение высшего профессионального образования «Поволжский государственный университет телекоммуникаций и информатики» КОЛЛЕДЖ СВЯЗИ УТВЕРЖДАЮ: Зам. директора по УПР _______Черненкова Н.В. «____»__________2011г. СБОРНИК Практических занятий
По дисциплине: «Элементы высшей математики» Номера работ: №1 – 16 для специальностей: 230115 – «Программирование в компьютерных системах» 230401 – «Информационные системы»
Каждая работа рассчитана на 2 часа
Составлен преподавателем Лобачевой М.Е. Рассмотрен на заседании П(Ц)К «Естественнонаучные и общепрофессиональные дисциплины» Протокол № 1 от 31.08.2011г. Председатель П(Ц)К________Лобачева М.Е.
Самара, 2011г Практическое занятие №1 Наименование занятия: Операции над матрицами. Вычисление определителей Цель занятия: Научиться выполнять действия с матрицами, вычислять определители. Подготовка к занятию: Повторить теоретический материал по теме «Матрицы и определители». Литература: 1. Григорьев В.П., Дубинский Ю.А. «Элементы высшей математики», 2008г. 2. Дадаян А.А. «Математика», 2004г. Задание на занятие:
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ Матрицей размера m´n, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i - номер строки, а j - номер столбца.
А = Транспонированной к матрице А называется матрица Например, А = Действия с матрицами 1) Умножение матрицы на число. Для того чтобы умножить матрицу 2) Сложение матриц. Складывать можно только матрицы с одинаковым числом строк и столбцов, т.е. матрицы одинаковых размеров. Суммой матриц Пример. Даны матрицы А = 2А =
3) Умножение матриц. Произведение матрицы Пример. Найти произведение матриц А = АВ = ВА = Пример. Найти произведение матриц А= АВ =
Определители Каждой квадратной матрице Правила вычисления определителей 2-го и 3-го порядков легко выписать:
Последнюю формулу, несмотря на внешнюю сложность записи, нетрудно запомнить. Если соединить линией каждые три элемента определителя, произведение которых входит в правую часть последней формулы со знаком «
Схема 1 Схема 2 Способы вычисления определителей: 1. Определитель можно вычислить, используя непосредственно его определение. Этим способом удобно вычислять определители второго и третьего порядка.
2. Определитель можно вычислить с помощью его разложения по элементам строки или столбца. 3. Определитель можно вычислить способом приведения к треугольному виду. Чтобы получить треугольный определитель, нужно к какой-либо строке (или столбцу) заданного определителя прибавлять соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, до тех пор, пока не придем к определителю треугольного вида. Пример. Вычислить определитель матрицы по правилу треугольников А =
= -5 + 18 + 6 = 19. Пример. Вычислить определитель с помощью его разложения по элементам первой строки.
Значение определителя: -1·10 + 3·2 – 4·10 = -44.
Практическое занятие №2 Наименование занятия: Нахождение обратной матрицы. Вычисление ранга матрицы. Цель занятия: Научиться находить обратные матрицы, вычислять ранг матриц. Подготовка к занятию: Повторить теоретический материал по теме «Матрицы и определители». Литература:
Задание на занятие:
1) 2) 3) 4) 5)
1) 2) Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ Обратная матрица Квадратная матрица А называется невырожденной, если ее определитель отличен от нуля. В противном случае матрица А называется вырожденной. Если А – квадратная матрица, то обратной по отношению к А называется матрица, которая при умножении на матрицу А (как слева, так и справа) дает единичную матрицу. Обратная матрица обозначается символом Если А – невырожденная матрица, то для нее существует обратная матрица
Пример. Дана матрица А = Найдем определитель матрицы. А 11 = 4; А 12 = – 3; А 21 = – 2; А 22 = 1 Таким образом, Ранг матрицы Минором порядка В матрице Рангом матрицы называется порядок базисного минора, или, иначе, самый большой порядок, для которого существуют отличные от нуля миноры. Вычисление ранга матрицы Идея практического метода вычисления ранга матрицы заключается в том, что с помощью элементарных преобразований данную матрицу приводят к треугольному виду. Тогда ранг матрицы будет равен числу ненулевых строк в полученной матрице. Элементарными преобразованиями называют следующие преобразования матриц:
1) Умножение или деление строки на число, отличное от нуля; 2) Сложение и вычитание строк; 3) Перестановку строк; 4) Вычеркивание (удаление) одной из одинаковых строк (столбцов); 5) Транспонирование Те же операции, применяемые для столбцов, также являются элементарными преобразованиями.
Пример: Определить ранг матрицы.
Если с помощью элементарных преобразований не удается найти матрицу, эквивалентную исходной, но меньшего размера, то нахождение ранга матрицы следует начинать с вычисления миноров наивысшего возможного порядка. В вышеприведенном примере – это миноры порядка 3. Если хотя бы один из них не равен нулю, то ранг матрицы равен порядку этого минора. Практическое занятие №3 Наименование занятия: Решение систем линейных уравнений матричным методом и методом Крамера. Цель занятия: Научиться решать системы линейных уравнений различными методами. Подготовка к занятию: Повторить теоретический материал по теме «Системы линейных уравнений» Литература:
Задание на занятие:
1)
2)
3) 4)
5)
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ Матричный метод и метод Крамера применимы только к тем системам линейных уравнений, в которых число неизвестных равняется числу уравнений. Пусть дана система Практическое занятие №4 Наименование занятия: Решение систем линейных уравнений методом Гаусса Цель занятия: Научиться решать системы линейных уравнений методом Гаусса Подготовка к занятию: Повторить теоретический материал по теме «Системы линейных уравнений» Литература:
Задание на занятие:
1)
2)
4)
5)
3)
6) Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ Рассмотрим произвольную систему линейных уравнений. Система m уравнений с n неизвестными в общем виде записывается следующим образом:
где aij – коэффициенты, а bi – постоянные. Решением системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество. Для этой системы линейных уравнений вида матрица
А =
А*= Метод Гаусса Суть метода заключается в том, что систему уравнений с помощью элементарных преобразований приводят к эквивалентной ей системе с треугольной матрицей (системы называются эквивалентными, если множества их решений совпадают). Эти действия называются прямым ходом. Затем из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратный ход). Элементарными преобразованиями систем являются: 1) Умножение или деление коэффициентов и свободных членов на одно и то же число 2) Сложение и вычитание уравнений 3) Перестановка уравнений системы местами. 4) Исключение из системы уравнений, в которых все коэффициенты при неизвестных и свободные члены равны нулю Пример. Решить систему линейных уравнений методом Гаусса Составим расширенную матрицу системы. А* = Выполним над этой матрицей следующие преобразования: 1) поменяем местами 1 и 2 строки; 2) прибавим к элементам 2 строки 1-ю строку, умноженную на -2; 3) прибавим к элементам 3 строки 1-ю строку, умноженную на -7; 4) прибавим к элементам 3 строки 2-ю строку, умноженную на -3; А* = Получили систему с треугольной матрицей. Таким образом, исходная система может быть представлена в виде:
Практическое занятие №5 Наименование занятия: Операции над векторами Цель занятия: Научиться выполнять действия с векторами Подготовка к занятию: Повторить теоретический материал по теме «Векторы. Операции над векторами» Литература:
Задание на занятие:
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ
Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевойвектор – это вектор, начало и конец которого совпадают. Длиной (модулем) вектора называется расстояние между началом и концом вектора.
Действия над векторами 1. Суммой двух векторов называется вектор 2. Произведением вектора 1) 2) вектор 3) вектор Координаты вектора Пусть точки А(х 1, y 1) и B(x 2, y 2), заданы в прямоугольной декартовой системе координат. Чтобы найти координаты вектора
Практическое занятие №6 Наименование занятия: Составление уравнений прямых. Цель занятия: Научиться составлять уравнения прямых. Подготовка к занятию: Повторить теоретический материал по теме «Прямая на плоскости» Литература:
Задание на занятие: 1. Составить уравнение прямой, проходящей через точку В(5; 3) и имеющей нормальный вектор 2. Составить уравнение прямой, проходящей через точку А(3; -2) и имеющей направляющий вектор 3. Треугольник задан точками А(5; 2), В(-1; -4), С(-5; -3). Составить уравнение прямой, проходящей через точку В параллельно АС. 4. Составить уравнение прямой, проходящей через точки А(1; 3), В(4; 1). 5. Составить уравнения медиан треугольника с вершинами А(7; 0), В(3; 6), С(-1; 1). 6. Составить уравнение прямой, проходящей через точку (2; 3) и перпендикулярной прямой 4 х + 3 у - 12 = 0. 7. Записать уравнения прямых в отрезках и построить их: а) 2 х + 5 у + 20 = 0; б) х – 8 у + 4 = 0. Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ
Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно, т.е. А 2 + В 2 ¹ 0. Это уравнение первого порядка называют общим уравнением прямой. Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий. Уравнение прямой в отрезках Если в общем уравнении прямой Ах + Ву + С = 0 коэффициент С ¹ 0, то, разделив на С, получим: Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.
Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках. А = -1, В = 1, С = 1, тогда а = -1, b = 1. Уравнение прямой в отрезках примет вид Пример. Даны вершины треугольника А(0; 1), B(6; 5), C(12; -1). Найти уравнение высоты, проведенной из вершины С. Находим уравнение стороны АВ: 4 x = 6 y – 6; 2 x – 3 y + 3 = 0; Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b. k = Ответ: 3 x + 2 y – 34 = 0.
Практическое занятие №7 Наименование занятия: Кривые второго порядка. Цель занятия: Научиться составлять кривых 2-го порядка, строить их. Подготовка к занятию: Повторить теоретический материал по теме «Кривые 2-го порядка» Литература:
Задание на занятие:
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ
Окружностью называется множество всех точек плоскости, равноудаленных от одной точки, называемой центром. Пусть центром окружности является точка О (a; b), а расстояние до любой точки М (х;у) окружности равно R. Тогда (x – a)2 + (y – b)2 = R 2 – каноническое уравнение окружности с центром О (a; b) и радиусом R.
Пример. Найти координаты центра и радиус окружности, если ее уравнение задано в виде: 2 x 2 + 2 y 2 – 8x + 5 y – 4 = 0. Для нахождения координат центра и радиуса окружности данное уравнение необходимо привести к каноническому виду. Для этого выделим полные квадраты: x 2 + y 2 – 4 x + 2,5 y – 2 = 0 x 2 – 4 x + 4 – 4 + y 2 + 2,5 y + 25/16 – 25/16 – 2 = 0 (x – 2)2 + (y + 5/4)2 – 25/16 – 6 = 0 (x – 2)2 + (y + 5/4)2 = 121/16 Отсюда находим координаты центра О (2; -5/4); радиус R = 11/4.
Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух заданных точек (называемых фокусами) есть величина постоянная, большая, чем расстояние между фокусами. Фокусы обозначаются буквами F 1, F 2, расстояние между фокусами – 2 с, сумма расстояний от любой точки эллипса до фокусов – 2 а (2 а > 2 c), a – большая полуось; b – малая полуось. Каноническое уравнение эллипса имеет вид: Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к длине большей оси и называется эксцентриситетом. Т.к. по определению 2 а > 2 c, то эксцентриситет всегда выражается правильной дробью, т.е.
Пример. Составить уравнение эллипса, если его фокусы F1(0; 0), F2(1; 1), большая ось равна 2. Уравнение эллипса имеет вид: Расстояние между фокусами: 2 c =
Гиперболой называется множество точек плоскости, разность расстояний от каждой из которых до двух заданных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами. Каноническое уравнение гиперболы имеет вид: Эксцентриситетом гиперболы называется отношение расстояния между фокусами к длине действительной оси: Если длина действительной оси равна длине мнимой оси, т.е. а = b, ε = Пример. Составить каноническое уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса с уравнением Находим фокусное расстояние c 2 = 25 – 9 = 16. Для гиперболы: c 2 = a 2 + b 2 = 16, ε = c/a = 2; c = 2 a; c 2 = 4 a 2; a 2 = 4; b 2 = 16 – 4 = 12. Тогда
Параболой называется множество точек плоскости, равноудаленных от заданной точки, называемой фокусом, и данной прямой, называемой директрисой. Фокус параболы обозначается буквой F, директриса – d, расстояние от фокуса до директрисы – р. Каноническое уравнение параболы, фокус которой расположен на оси абсцисс, имеет вид: y 2 = 2 px или y 2 = -2 px Уравнения директрис соответственно x = - p /2, x = p /2 Каноническое уравнение параболы, фокус которой расположен на оси ординат, имеет вид: х 2 = 2 pу или х 2 = -2 pу Уравнения директрис соответственно у = - p /2, у = p /2 Пример. На параболе у 2 = 8 х найти точки, расстояние которой от
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 618; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.203.158 (0.013 с.) |

 и
и  . Найти матрицу С = 5А – 2В.
. Найти матрицу С = 5А – 2В. и
и  . Найти матрицу С = АТ·В.
. Найти матрицу С = АТ·В. и
и  . Найти матрицу С = А·В.
. Найти матрицу С = А·В.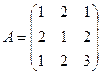 и
и  . Найти матрицу С = А·В – В·А.
. Найти матрицу С = А·В – В·А.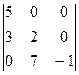 .
. .
.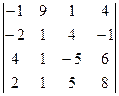 .
.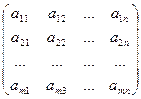
 , у которой строки и столбцы меняются местами.
, у которой строки и столбцы меняются местами.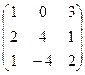 , AT =
, AT = 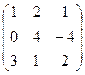 ;
; на число
на число  , нужно каждый элемент матрицы
, нужно каждый элемент матрицы  умножить на это число:
умножить на это число:  .
. называется матрица
называется матрица  , элементы которой равны суммам соответствующих элементов матриц
, элементы которой равны суммам соответствующих элементов матриц  и
и 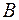 , т.е.
, т.е. 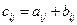 для любых индексов i, j.
для любых индексов i, j. ; B =
; B =  , найти 2А + В.
, найти 2А + В.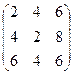 , 2А + В =
, 2А + В = 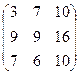 .
. ) определено только в том случае, когда число столбцов матрицы
) определено только в том случае, когда число столбцов матрицы  , у которой столько же строк, сколько их в матрице
, у которой столько же строк, сколько их в матрице  и В =
и В =  .
.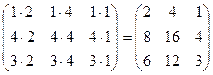 .
. , В =
, В = 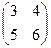
 =
= 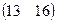 .
. или
или  . При этом порядком определителя называют порядок соответствующей матрицы.
. При этом порядком определителя называют порядок соответствующей матрицы. ,
,
 », то получим легко запоминающуюся схему 1. Аналогично для произведений, входящих со знаком «–», имеем схему 2.
», то получим легко запоминающуюся схему 1. Аналогично для произведений, входящих со знаком «–», имеем схему 2.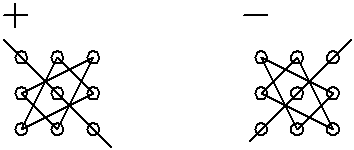


 = -1
= -1 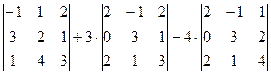
 ;
; ;
; ;
; ;
;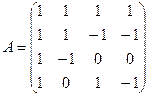
 ;
;
 .
. , которая вычисляется по формуле
, которая вычисляется по формуле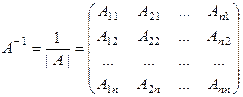 , где
, где 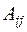 – алгебраическое дополнение элемента
– алгебраическое дополнение элемента  .
. , найти А-1.
, найти А-1. = 4 – 6 = – 2 ≠ 0, следовательно, для этой матрицы существует обратная. Найдем алгебраические дополнения к элементам матрицы:
= 4 – 6 = – 2 ≠ 0, следовательно, для этой матрицы существует обратная. Найдем алгебраические дополнения к элементам матрицы: .
. матрицы
матрицы 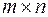 минор порядка
минор порядка  равны нулю или миноров порядка
равны нулю или миноров порядка  вообще нет, т.е.
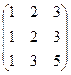
вообще нет, т.е.  ~
~ 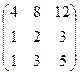 ~
~  ~
~  ,
,  Rg = 2.
Rg = 2.

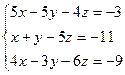
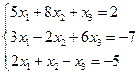

 линейных уравнений с
линейных уравнений с 






 ,
, называется матрицей системы, а матрица
называется матрицей системы, а матрица называется расширенной матрицей системы
называется расширенной матрицей системы
 .
.
 , откуда получаем: x 3 = 2; x 2 = 5; x 1 = 1.
, откуда получаем: x 3 = 2; x 2 = 5; x 1 = 1. и
и  . Построить векторы
. Построить векторы  ,
,  .
. ,
,  ,
,  , если А (2; 3), В (-1; -3), С (-7; 5).
, если А (2; 3), В (-1; -3), С (-7; 5). ,
,  ,
,  ,
, 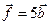 .
. .
.
 совпадет с началом вектора
совпадет с началом вектора  , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям: ;
; нужно из координат его конца вычесть координаты начала т.е.
нужно из координат его конца вычесть координаты начала т.е. 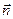 (5; 0).
(5; 0). или
или  , где
, где 
 .
. ;
;
 . Тогда y =
. Тогда y =  . Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению:
. Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению:  откуда b = 17. Итого:
откуда b = 17. Итого:  .
. = 8.
= 8. .
. , где a, b и c связаны между собой равенствами: a2 – b2 = c2 (или b2 – a2 = c2).
, где a, b и c связаны между собой равенствами: a2 – b2 = c2 (или b2 – a2 = c2). или
или  .
. .
. , таким образом, a 2 – b 2 = c 2 =
, таким образом, a 2 – b 2 = c 2 =  . По условию 2 а = 2, следовательно, а = 1, b =
. По условию 2 а = 2, следовательно, а = 1, b =  Искомое уравнение эллипса примет вид:
Искомое уравнение эллипса примет вид:  .
. или
или  , где a, b и c связаны между собой равенством a2 + b2 = c2. Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат. Фокусы обозначаются буквами F 1, F 2, расстояние между фокусами – 2 с, разность расстояний от любой точки гиперболы до фокусов – 2 а (2 а < 2 c). Ось 2 а называется действительной осью гиперболы, ось 2 b – мнимой осью гиперболы. Гипербола имеет две асимптоты, уравнения которых
, где a, b и c связаны между собой равенством a2 + b2 = c2. Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат. Фокусы обозначаются буквами F 1, F 2, расстояние между фокусами – 2 с, разность расстояний от любой точки гиперболы до фокусов – 2 а (2 а < 2 c). Ось 2 а называется действительной осью гиперболы, ось 2 b – мнимой осью гиперболы. Гипербола имеет две асимптоты, уравнения которых 
 .
. , то гипербола называется равносторонней.
, то гипербола называется равносторонней.
 - искомое уравнение гиперболы.
- искомое уравнение гиперболы.


