
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точность систем регулирования по возмущающим воздействиямСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Точность регулирования оценивают по ошибкам, с которыми воспроизводятся заданные значения регулируемых величин. Чем выше точность регулирования, тем меньше должны быть эти ошибки. В одной и той же системе ошибки получаются различными в зависимости от того, каким воздействием задающим, возмущающим или и тем и другим одновременно они вызваны. Ошибки одномерной системы считаются по формулам:
Wp- передаточная функция регулятора; Wo- передаточная функция объекта регулирования;
Входные воздействия в виде ступенчатого сигнала, скачков скорости и ускорения, гармонического и стохастического сигналов Входное воздействие (Х) – воздействие, подаваемое на вход системы или устройства. Задающее воздействие (то же, что входное воздействие х) - воздействие на систему, определяющее требуемый закон изменения регулируемой величины). При исследовании АСУ и их элементов используют ряд стандартных сигналов, называемых типовыми воздействиями. Эти воздействия описываются простыми математическими функциями и легко воспроизводятся при исследовании АСУ. Использование типовых воздействий позволяет унифицировать анализ различных систем и облегчает сравнение их передаточных свойств. Наибольшее применение в ТАУ находят следующие типовые воздействия: · ступенчатое; · импульсное; · гармоническое; · линейное. Ступенчатое воздействие – воздействие, которое мгновенно возрастает от нуля до некоторого значения и далее остается постоянным (рис. 2.2, а). Ступенчатому воздействию соответствует функция
При анализе и расчете систем удобно использовать ступенчатое воздействие, у которого величина а0 = 1. Его называют единичным ступенчатым воздействием и обозначают 1 (t). Математическое выражение, описывающее единичное ступенчатое воздействие, имеет вид
Любое неединичное ступенчатое воздействие можно обозначить а0 1 (t). Единичное ступенчатое воздействие, возникающее в момент времени t – t1, обозначают 1 (t – t1). Ступенчатое воздействие чаще всего используют при исследованиях систем стабилизации параметров, так как эти воздействия наиболее близки к реальным входным (задающим и возмущающим) воздействиям систем стабилизации. Импульсное воздействие – одиночный импульс прямоугольной формы (рис. 2.2, б), имеющий достаточно большую высоту и малую длительность (по сравнению с инерционностью испытываемой системы) с площадью а0. При математическом анализе АСУ используют единичное импульсное воздействие, описываемое так называемой дельта-функцией
причем
Последние два выражения позволяют рассматривать дельта-функцию, как импульс, имеющий бесконечно большую высоту, бесконечно малую длительность и единичную площадь. Дельта-функцию можно определить также как производную единичного ступенчатого воздействия:
Неединичное импульсное ступенчатое воздействие с площадью а0 обозначается x(t) = а0 d (t). Гармоническое воздействие – сигнал синусоидальной формы, описываемый функцией (рис. 2.2, в) x(t) = xm sinw t, где xm – амплитуда сигнала; w = 2p / Т – круговая частота; Т – период сигнала.
Гармонический сигнал, начинающий действовать в момент времени t = 0, описывают при помощи единичной ступенчатой функции: x(t) = 1 (t) xm sinw t, Линейное воздействие – воздействие, описываемое функцией (рис. 2.2, г) x(t) = 1 (t) а1 t, Коэффициент а1 характеризует скорость нарастания воздействия x(t).
Устойчивость линейных САР Важным показателем АСР является устойчивость, поскольку основное ее назначение заключается в поддержании заданного постоянного значения регулируемого параметра или изменении его по определенному закону. При отклонении регулируемого параметра от заданной величины (например, под действием возмущения или изменения задания) регулятор воздействует на систему таким образом, чтобы ликвидировать это отклонение. Если система в результате этого воздействия возвращается в исходное состояние или переходит в другое равновесное состояние, то такая система называется устойчивой. Если же возникают колебания со все возрастающей амплитудой или происходит монотонное увеличение ошибки е, то система называется неустойчивой.
Необходимое и достаточное условие устойчивости формулируется следующим образом: Звено или система называются устойчивыми, если переходная составляющая с течением времени стремится к нулю:
Если выходной сигнал звена или системы y(t) рассматривать как сумму двух составляющих y(t) = yуст + уп(t), где
Рисунок 1.40 Если уп(t) с течением времени стремится к бесконечности, звено или система называются неустойчивыми. Другими словами:
Примеры переходных процессов для каждого случая приведены на рисунке 1.41.
Рисунок 1.41 Для того, чтобы определить, устойчива система или нет, используются критерии устойчивости: 1) корневой критерий; 2) критерий Стодола; 3) критерий Гурвица; 4) критерий Найквиста; 5) критерий Михайлова и др. Первые два критерия являются необходимыми критериями устойчивости отдельных звеньев и разомкнутых систем, однако не являются достаточными для однозначного определения устойчивости. Критерий Гурвица является алгебраическим и может быть использован для определения устойчивости как отдельных звеньев, так и замкнутых систем без запаздывания. При этом он позволяет обойтись без определения корней характеристического полинома, который может иметь достаточно большую степень. Последние два критерия относятся к группе частотных критериев, поскольку определяют устойчивость замкнутых систем по их частотным характеристикам. Их особенностью является возможность применения к замкнутым системам с запаздыванием, которыми является подавляющее большинство систем управления.
39 Критерий устойчивости (Гурвица) Критерий Гурвица, как и критерий Стодола, определяет устойчивость по характеристическому полиному системы без непосредственного вычисления его корней. Однако критерий Стодола является необходимым критерием устойчивости, но не является достаточным. То есть, если по критерию Стодола система неустойчива, то она действительно является неустойчивой, если по критерию система устойчива, то для подтверждения ее устойчивости требуются дополнительные расчеты. Например, характеристический полином s3 + s2 + 2s + 8 по критерию Стодола соответствует устойчивой системе, однако корни этого полинома равны s1 = -2, s2,3 = 0,5 ± j×1,94. То есть система фактически является неустойчивой, хотя коэффициенты полинома положительны. Критерий Гурвица дает необходимое и достаточное условие устойчивости линейных систем. Исходной информацией для данного критерия является характеристический полином системы: разомкнутой A(s) или замкнутой D(s) – в зависимости от того, какая система анализируется. Для определения устойчивости по Гурвицу строится матрица таким образом, чтобы по главной диагонали были расположены коэффициенты ХПЗС с an+1 по a0. Справа и слева от нее записываются коэффициенты с индексами через 2 (a0, a2, a4… или a1, a3, a5 …). Тогда для устойчивой системы необходимо и достаточно, чтобы определитель и все главные диагональные миноры матрицы были больше нуля. Если хотя бы один определитель будет равен нулю, то система будет находиться на границе устойчивости. Если хотя бы один определитель будет отрицателен, то система неустойчива независимо от числа положительных или нулевых определителей. Пример. Дана передаточная функция разомкнутой системы
Требуется определить устойчивость замкнутой системы по критерию Гурвица. Для этого определяется ХПЗС: D(s) = A(s) + B(s) = 2s4 + 3s3 + s2 + 2s3 + 9s2 + 6s + 1 = 2s4 + 5s3 + 10s2 + 6s + 1. Поскольку степень ХПЗС равна n = 4, то матрица будет иметь размер 4х4. Коэффициенты ХПЗС равны а4 = 2, а3 = 5, а2 = 10, а1 = 6, а0 = 1. Матрица имеет вид
(обратите внимание на сходство строк матрицы: 1 с 3 и 2 с 4). Определители (диагональные миноры матрицы): Δ1 = 5 > 0,
Δ4 = 1* Δ3 = 1*209 > 0. Поскольку все определители положительны, то АСР устойчива.
40 Критерий устойчивости (Найквиста) Данный критерий определяет устойчивость по частотным характеристикам системы. Для построения частотных характеристик, например, АФХ требуется подстановка s = jw в передаточную функцию системы, которая, как правило, представляет собой дробно-рациональную функцию. Поэтому данный критерий более сложен для ручного расчета по сравнению с критерием Михайлова. Последовательность: 1) Определяется передаточная функция разомкнутой системы 2) Определяется число правых корней m. 3) Подставляется s = jw: W¥(jw). 4) Строится АФХ разомкнутой системы. Для устойчивости АСР необходимо и достаточно, чтобы при увеличении w от 0 до ¥ АФХ W¥(jw) m раз полуохватывала точку (-1; 0), где m - число правых корней разомкнутой системы, т.е. корней si > 0.
Если АФХ проходит через точку (-1; 0), то замкнутая система находится на границе устойчивости (см. рисунок 1.45). В случае, если характеристическое уравнение разомкнутой системы A(s) = 0 правых корней не имеет (т.е. m = 0), то критерий можно переформулировать: замкнутая система устойчива, если АФХ разомкнутой системы W¥(jw) не охватывает точку (-1; 0), в противном случае система неустойчива; если проходит через нее, то на границе устойчивости. Пример. Пусть передаточная функция разомкнутой системы имеет вид
Для построения АФХ разомкнутой системы делается подстановка s = j*w в передаточную функцию:
где
а = (1 – 2*w2)2 + (3,5w3 – 4*w)2 – знаменатель.
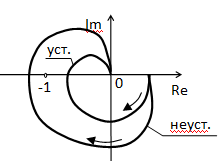
По полученным формулам строится АФХ (см. таблицу 1.4 и рисунок 1.46). Характеристическое уравнение правых корней не имеет, АФХ охватывает точку (-1; 0), следовательно, замкнутая система неустойчива. По виду амплитудно-фазовой частотной характеристики разомкнутой системы регулирования можно судить об её устойчивости в замкнутом состоянии. Метод, дающий возможность проводить такие суждения, был предложен в 1932 г. Найквистом применительно к радиотехническим системам при исследовании усилителей с отрицательной обратной связью. Критерий Найквиста называют амплитудно-фазовым критерием устойчивости. Для систем, устойчивых в разомкнутом состоянии, этот критерий формулируется следующим образом: для того, чтобы система регулирования, устойчивая в разомкнутом состоянии, была устойчива и замкнутом состоянии, необходимо и достаточно, чтобы годограф вектора амплитудно-фазовой частотной характеристики разомкнутой системы
|
||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 1601; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.013 с.) |


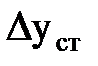 - статическая ошибка;
- статическая ошибка; - динамическая ошибка;
- динамическая ошибка;





 (-¥ < t < ¥),
(-¥ < t < ¥),
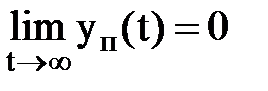 .
. - установившееся значение y(t), уп(t) – переходная составляющая, то уп(t) = y(t) – yуст.
- установившееся значение y(t), уп(t) – переходная составляющая, то уп(t) = y(t) – yуст.
 .
.
 .
.
 ,
,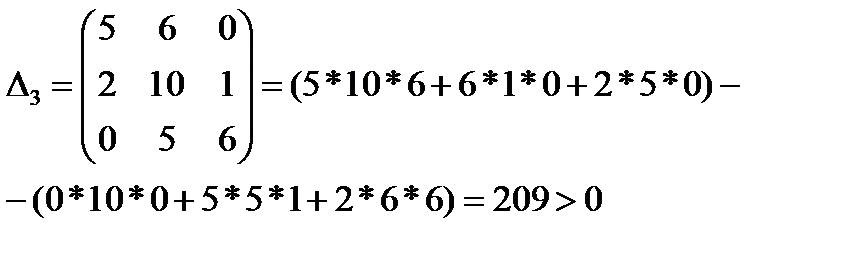
 .
.
 .
.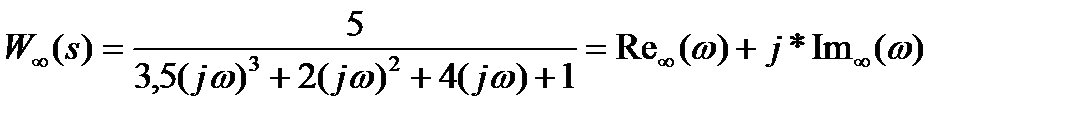 ,
, - действительная часть АФХ,
- действительная часть АФХ,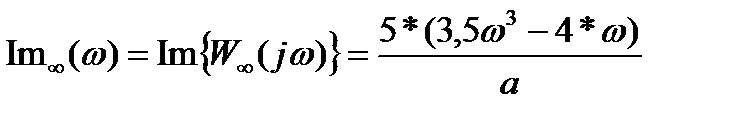 - мнимая часть,
- мнимая часть,
 не охватывал точку с координатой -1 на вещественной оси.
не охватывал точку с координатой -1 на вещественной оси.


