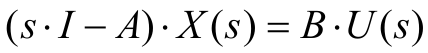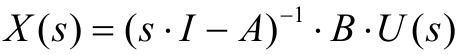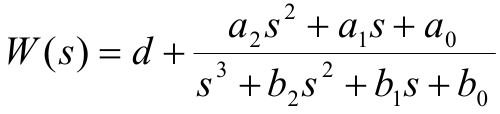Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Запасы устойчивости замкнутой системыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Запасы устойчивости легко определяются по логарифмических частотным характеристикам:
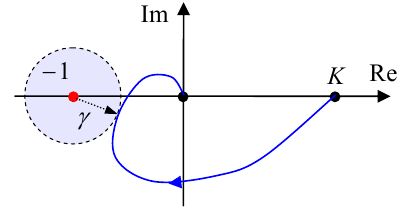
Заметим, что запас по амплитуде может быть равен бесконечности, если фазовая характеристика не пересекает линию ° −180. К сожалению, в некоторых случаях классические запасы устойчивости (по амплитуде и фазе) дают не совсем верное представление о том, насколько система действительно близка к границе устойчивости. Поэтому в качестве единой характеристики иногда используют кратчайшее расстояние γ от годографа до точки (−1;0).
Передаточная функция и пространство состояний Пространство состояний в теории управления используется для исследования устойчивости. Используя преобразование Лапласа, можно построить передаточную функцию для модели объекта в пространстве состояний
здесь u(t),y(t) и x(t) обозначают соответственно вход, выход и вектор состояния объекта. Преобразуя левые и правые части каждого уравнения по Лапласу (переходя к изображениям сигналов по Лапласу при нулевых начальных условиях), получаем
В первом уравнении перенесем все члены, зависящие от X(s),в левую часть:
где I обозначает единичную матрицу, у которой на главной диагонали стоят единицы, а все остальные элементы – нули. Умножая обе части последнего равенства на (s*I-A)-1, получим выражение для X(s):
которое при подстановке во второе уравнение в (1) дает
Чтобы определить передаточную функцию, найдем отношение изображений выхода и входа:
Обратный переход, от передаточной функции к модели в пространстве состояний, более сложен и неоднозначен. Дело в том, что каждой передаточной функции соответствует бесчис- ленное множество моделей в пространстве состояний. Одну из них можно найти следующим образом. Для передаточной функции
где d,ai (i=0,1,2) и bi (i=0,1,2) – постоянные коэффициенты, модель в пространстве состояний задается матрицами
Точность САР Точность регулирования оценивают по ошибкам, с которыми воспроизводятся заданные значения регулируемых величин. Чем выше точность регулирования, тем меньше должны быть ошибки. В одной и той же системе ошибки получаются различными различными в зависимости от того, каким воздействием задающим, возмущающим или тем и другим одновременно они вызваны. Систему, контур которой не имеет интегрирующих звеньев, называют статической, а при наличии в системе одного или нескольких интегрирующих звеньев – астатической. По числу интегр-их зв-ев определяют порядок астатизма системы, при одном – астатизм первого порядки и т.д. Для определения ошибок в установившемся режиме (при t->∞):
где K, K1 – коэффициент усиления всей разомкн. системы и коэф усил-ия объекта Для систем с астатизмом υ изображение ошибки в установивш. режиме имеет вид: При отсутствии в системе интегрирующих звеньев постоянные воздействия g0 и f0 вызывают постоянную пищьмищьку ε0, которую называют статической. Эта ошибка будет тем меньше, чем больше коэффициент усиления К системы, причем для уменьшения статической ошибки, вызванной возмущающим воздействием, следует увеличить K2 регулятора, а не K1 объекта. В системе с астатизмом первого порядка установившаяся ошибка возникает при воздействиях с постоянной скоростью. Такая ошибка называется скоростной. При воздействиях с постоянным ускорением в системе с астатизмом второго порядка возникает ошибка по ускорению.
|
||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 1019; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.007 с.) |


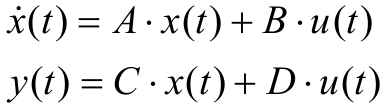
 (1)
(1)