
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальное уравнение САР и их линеаризация.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Известно, что любое движение, процессы передачи, обмена, преобразования энергии и вещества математически можно описать в виде дифференциальных уравнений (ДУ). Любые процессы в АСР также можно описать дифференциальными уравнениями, которые определяют сущность происходящих в системе процессов независимо от ее конструкции и т.д. Решив ДУ, можно найти характер изменения регулируемой переменной в переходных и установившихся режимах при различных воздействиях на систему. Для упрощения задачи нахождения ДУ, описывающего работу АСР в целом, систему разбивают на ее отдельные элементы, переходные процессы в которых описываются достаточно простыми ДУ. Так как ДУ описывают работу системы независимо от физической сущности протекающих в ней процессов, то при декомпозиции системы нет необходимости учитывать их физическую целостность. Для каждого элемента структурной схемы необходимо составить ДУ, определяющее зависимость изменения выходной величины от входной. Так как выходная величина предыдущего элемента является входной для последующего, то, определив ДУ отдельных элементов, можно найти ДУ системы. Однако такой метод применим только в частных случаях. Дело в том, что в большинстве случаев в реальных элементах системы связь междувходной и выходной величинами является нелинейной и часто задается в графической форме. Поэтому, даже если ДУ системы и будет получено, оно будет нелинейным. А аналитическое решение нелинейных ДУ возможно далеко не всегда. Для решения этой проблемы учитывают, что в процессе регулирования отклонения всех изменяющихся величин от их установившихся значений малы, и поэтому возможна замена нелинейных ДУ приближенными линейными ДУ, то есть возможна линеаризация дифференциальных уравнений.
Рассмотрим сущность процесса линеаризации на примере сушильного шкафа. Зависимость температуры объекта от подаваемого напряжения в большинстве случаев нелинейна и имеет вид, представленный на рисунке. Графически линеаризацию некоторого уравнения от двух переменных F(х,у) = 0 в окрестности некоторой точки (х0, у0) можно представить как замену рассматриваемого участка кривой на касательную, уравнение которой определяется по формуле
где Линеаризация ДУ происходит аналогично, отличие состоит только в том, что необходимо искать частные производные по производным ( Пример. Линеаризация нелинейного ДУ. 3xy - 4x2 + 1,5 Данное ДУ является нелинейным из-за наличия произведений переменных х и у. Линеаризируем его в окрестности точки с координатами х0 = 1, 3у0 - 4 + 0 = 0 + у0, откуда у0 = 2. Введем в рассмотрение функцию F = 3xy - 4x2 + 1,5x’y - 5y’ - y и определим все ее производные при заданных начальных условиях:
Теперь, используя полученные коэффициенты, можно записать окончательное линейное ДУ: -5.Dy’ + 2.Dy + 3.Dх’ - 2.Dх = 0. Линеаризация ДУ, заданного в явном виде относительно у, т.е. y = F(x) производится по формуле
то есть в данном случае нет необходимости искать производные по у. Структурные схемы. Для исследования и расчета структурную схему АСР путем эквивалентных преобразований приводят к простейшему стандартному виду «объект - регулятор». Практически все инженерные методы расчета и определения параметров настройки регуляторов применены для такой стандартной структуры. В общем случае любая одномерная АСР с главной обратной связью путем постепенного укрупнения звеньев может быть приведена к такому виду. Если выход системы у не подавать на ее вход, то получается разомкнутая система регулирования, передаточная функция которой определяется как произведение: W¥ = Wp.Wy (Wp - ПФ регулятора, Wy - ПФ объекта управления).
То есть последовательность звеньев Wpи Wy может быть заменена одним звеном с W¥. Передаточную функцию замкнутой системы принято обозначать как Ф(s). Она может быть выражена через W¥: Фз(s) = (далее будем рассматривать только системы с обратной отрицательной связью, поскольку они используются в подавляющем большинстве АСР).
Данная передаточная функция Фз(s) определяет зависимость у от х и называется передаточной функцией замкнутой системы по каналу задающего воздействия (по заданию). Для АСР существуют также передаточные функции по другим каналам: Фe(s) = Фв(s) = где Wу.в.(s) – передаточная функция объекта управления по каналу передачи возмущающего воздействия. В отношении учета возмущения возможны два варианта: - возмущение оказывает аддитивное влияние на управляющее воздействие; - возмущение влияет на измерения регулируемого параметра. Примером первого варианта может быть влияние колебаний напряжения в сети на напряжение, подаваемое регулятором на нагревательный элемент объекта. Пример второго варианта: погрешности при измерениях регулируемого параметра вследствие изменения температуры окружающей среды. Wу.в.–модель влияния окружающей среды на измерения.
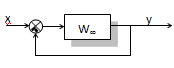
Для первого варианта передаточная функция Wу.в. принимается равной Wу, для второго – как правило, на схеме она выделена в отдельное звено. Поскольку передаточная функция разомкнутой системы является в общем случае дробно-рациональной функцией вида W¥ = Фз(s) = Фe(s) = гдеD = A + B. Как видно, эти передаточные функции отличаются только выражениями числителей. Выражение знаменателя называется характеристическим выражением замкнутой системы и обозначается как Dз(s) = A(s) + B(s), в то время как выражение, находящееся в знаменателе передаточной функции разомкнутой системы W¥, называется характеристическим выражением разомкнутой системы А(s). Пример. Определение передаточных функций АСР. Структура АСР представлена на рисунке. Требуется определить передаточные функции регулятора, объекта, разомкнутой системы, замкнутой системы и характеристические выражения.
ПараметрыK0 = 1, K1 = 3, K2 = 1,5,K4 = 2, K5 = 0,5. В структурной схеме АСР звенья, соответствующие регулирующему устройству, стоят перед звеньями объекта управления и генерируют управляющее воздействие на объект u. По схеме видно, что к схеме регулятора относятся звенья 1, 2 и 3, а к схеме объекта – звенья 4 и 5. Учитывая, что звенья 1, 2 и 3 соединены параллельно, получаем передаточную функцию регулятора как сумму передаточных функций звеньев:
Звенья 4 и 5 соединены последовательно, поэтому передаточная функция объекта управления определяется как произведение передаточных функций звеньев:
Передаточная функция разомкнутой системы:
откуда видно, что числитель В(s) = 1,5.s2 + 3.s + 1, знаменатель (он же характеристический полином разомкнутой системы) А(s) = 2.s3 + 3.s2 + s. Тогда характеристический полином замкнутой системы равен: D(s) = A(s) + B(s) = 2.s3 + 3.s2 + s + 1,5.s2 + 3.s + 1 = 2.s3 + 4,5.s2 + 4.s + 1. Передаточные функции замкнутой системы: по заданию по ошибке При определении передаточной функции по возмущению принимается Wу.в. = Wоу. Тогда
|
||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 932; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.192.113 (0.01 с.) |


 ,
, и
и  - частные производные от F по х и у. Данное уравнение называется уравнением в приращениях, поскольку значения х и у здесь заменены на приращения Dх = х - х0 и Dу = у - у0.
- частные производные от F по х и у. Данное уравнение называется уравнением в приращениях, поскольку значения х и у здесь заменены на приращения Dх = х - х0 и Dу = у - у0.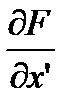 ,
,  ,
,  и т.д.). Итоговое уравнение в приращениях будет содержать приращения производных: Dх’ = х’– х’0, Dх” = х”– х”0, …, Dy’ = y’–y’0, Dy” = y”–y”0, и т.д.
и т.д.). Итоговое уравнение в приращениях будет содержать приращения производных: Dх’ = х’– х’0, Dх” = х”– х”0, …, Dy’ = y’–y’0, Dy” = y”–y”0, и т.д. y = 5
y = 5  + y
+ y = 0,
= 0,  = 0. Для определения недостающего начального условия у0 подставим данные значения в ДУ:
= 0. Для определения недостающего начального условия у0 подставим данные значения в ДУ: = (3у - 8х
= (3у - 8х  = 3*2 - 8*1 = -2,
= 3*2 - 8*1 = -2,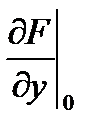 = (3х + 1,5x’ - 1
= (3х + 1,5x’ - 1  = (1,5у
= (1,5у  = -5.
= -5. ,
,
 =
=  .
. =
=  - по ошибке,
- по ошибке, =
=  - по возмущению,
- по возмущению,
 , то передаточные функции замкнутой системы могут быть преобразованы:
, то передаточные функции замкнутой системы могут быть преобразованы: =
=  =
=  ,
, =
=  =
= 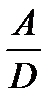 ,
,
 .
. .
. ,
, ,
,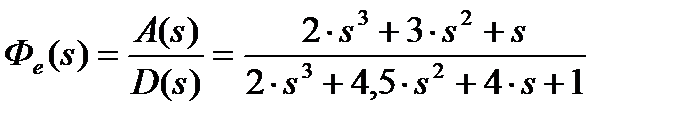 .
. .
.


