Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи, приводящие к интегральным уравнениям ВольтерраСодержание книги
Поиск на нашем сайте Задача o таутохроне Найти кривую, скользя вдоль которой без трения тяжелая частица достигает своего самого низкого положения за одно и то же время независимо от её начального положения.
Решение. Выполним чертеж
и введем обозначения Далее воспользовавшись формулой из физики
и формулами из курса математического анализа
подставим формулы (2.2) в равенство (2.1)
Введем обозначение
Полученное равенство (2.3) проинтегрируем по t (0≤ t ≤ T), в то же время
откуда
Интегральное уравнение вида (2.4) есть уравнение Вольтерра первого рода, где u(x) - неизвестная функция. Решение таких уравнений впервые предложил Абель и поэтому уравнения такого вида называются уравнениями Абеля.
Задачи Коши для дифференциальных уравнений первого порядка
Формально проинтегрировав уравнение в задаче (2.5) с пределами интегрирования от
которое эквивалентно задаче (2.5).
Задача Коши для линейных уравнений Высших порядков
Положим
тогда
где
и по формуле Коши для кратного интегрирования имеем
…………………………………………………………
………………………………………………………
Найдем дифференциальный оператор
Введем обозначения
Тогда выражение для дифференциального оператора
и вводя обозначение g(x) = f(x) –
которое эквивалентно первоначальной задаче.
Краевые задачи для дифференциальных уравнений Рассмотрим линейную краевую задачу
где Как и в предыдущей задаче введем новую функцию
и выпишем выражения производных и самой функции y(x)
Если в (2.11) положить
При
Подставляем выражения для производных
Обозначим определитель этой системы через
Пусть
. Найдем выражение дифференциального оператора
где
Подставляя выражение (2.16) в уравнение краевой задачи(2.10), придем к разрешающему интегральному уравнению смешанного типа Вольтерра-Фредгольма
где F(x) = f(x) – Ф (x). Полученное разрешающее уравнение эквивалентно первоначально поставленной краевой задаче (2.10). Аналогичных задач в различных областях знаний возникает множество, мы ограничимся приведёнными.
Интегральные уравнения Вольтера Как частный случай уравнений Фредгольма Интегральные уравнения Вольтерра как первого так и второго рода
при некоторых ограничениях можно рассматривать как частный случай уравнений Фредгольма. Чтобы показать это построим новое ядро
и запишем интегральное уравнение Фредгольма с этим ядром
Ядро H(x,t) равно нулю вне заштрихованной части квадрата, по которой берётся Фредгольмовский интеграл и оба интеграла вычисляются по заштрихованной области, следовательно, они равны т.е.
Однако интегральные урравнения Вольтерра обладают свойствами характерными только для них. Для них применимы некоторые методы решения и исследования, которые не применимы или имеют существенные ограничения для уравнений Фредгольма.
Пример 1. Для интегрального уравнения Вольтерра второго рода
записать эквивалентное интегральное уравнение Фредгольма.
Решение. Строим ядро
и записываем уравнение Фредгольма с этим ядром
которое и будет эквивалентным данному.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1200; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.008 с.) |


 , Т – постоянная величина,
, Т – постоянная величина,  - функция от h, кривую будем искать в виде
- функция от h, кривую будем искать в виде 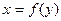 .
. (2.1)
(2.1) , где
, где 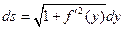 , (2.2)
, (2.2) , откуда
, откуда  .
.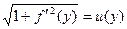 и так как с течением времени функция s(t) убывает, то оставляем знак минус
и так как с течением времени функция s(t) убывает, то оставляем знак минус . (2.3)
. (2.3)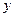 изменяется от h до 0 (h ≥
изменяется от h до 0 (h ≥ 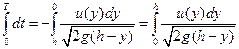 ,
,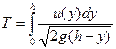 . (2.4)
. (2.4)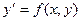 ,
, 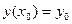 . (2.5)
. (2.5) до x получим нелинейное уравнение Вольтерра второго рода
до x получим нелинейное уравнение Вольтерра второго рода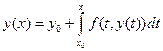 ,
,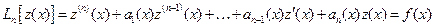 ,
,  ,
, 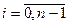 , где
, где  . (2.6)
. (2.6)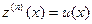 (2.7)
(2.7) ,
, – любое из отрезка [ a, b ] при нахождении общего решения и
– любое из отрезка [ a, b ] при нахождении общего решения и 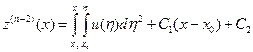
 ,
,
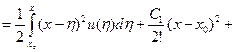

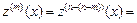
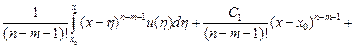
 ,
,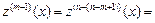
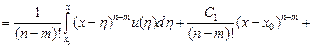
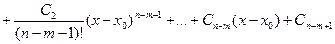 ,
,
 ,
,
 . (2.8)
. (2.8)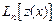 , подставив в него полученные выражения для функции
, подставив в него полученные выражения для функции 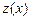 и её производных
и её производных 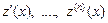



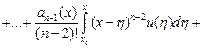





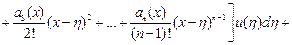



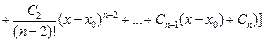 .
.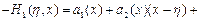
 ,
,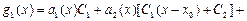


 .
.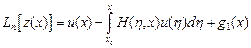
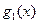 придем к разрешающему интегральному уравнению
придем к разрешающему интегральному уравнению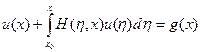 , (2.9)
, (2.9)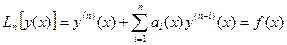 ,
, ,
,  , (2.10)
, (2.10)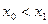 , функции
, функции  и
и 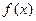 – непрерывны
– непрерывны  коэффициенты
коэффициенты 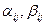 и
и 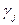 – постоянные числа.
– постоянные числа.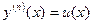
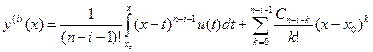 , (2.11)
, (2.11)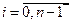 , где
, где  .
. , то получим
, то получим 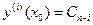 и соотношения (2.11) перепишутся
и соотношения (2.11) перепишутся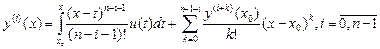 . (2.12)
. (2.12)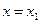 из (2.11) имеем
из (2.11) имеем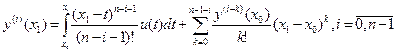 . (2.13)
. (2.13)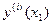 (2.13) в краевые условия (2.10)
(2.13) в краевые условия (2.10)
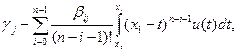
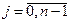 или, группируя члены с одноимёнными производными, получим систему n линейных неоднородных алгебраических уравнений с неизвестными
или, группируя члены с одноимёнными производными, получим систему n линейных неоднородных алгебраических уравнений с неизвестными 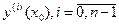 .
.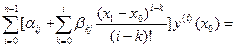

 . (2.14)
. (2.14)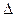
 .
. (2.15)
(2.15) через новую функцию
через новую функцию 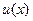
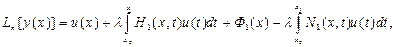 (2.16)
(2.16)


 .
.

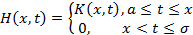 !!!
!!! .
.