
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегральные уравнения Вольтерра с вырожденными ядрамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Уравнения Вольтерра второго рода 2.
Введем обозначения
Тогда уравнение (7.1) перепишется
Дифференцируя равенство (7.2)
и учитывая равенство (7.3), придем к системе линейных дифференциальных уравнений для определения функции
Если удастся найти решение системы (7.4) с этими начальными условиями, то решение интегрального уравнения (7.1) определиться по формуле (7.3) или с помощью любого из выражений
которое получается дифференцированием формул (7.2).
Пример 7. Решим уравнение
Решение. При
откуда находим
Подставив полученное выражение для интеграла в исходное уравнение придем к дифференциальному уравнению
По формуле решения линейного однородного дифференциального уравнения первого порядка находим общее решение
Определить значение
при значениях Ответ:
Проверим, что найденная функция удовлетворяет исходному уравнению
т. е.имеем тждество
где условие Аналогично, как и в предыдущем случае вводим неизвестные функции
и дифференцируем это равенство
Затем дифференцируем исходное уравнение
откуда находим
Выразив
с начальными условиями Если удастся найти решение системы (7.9) с этими начальными условиями, то решение определиться по формуле (7.7)
при любом Значительно проще вопрос решается, если вырожденное ядро состоит из одного слагаемого
при аналогичном условии Как и ранее вводим новую функцию
и дифференцируем ее
Затем дифференцируем исходное уравнение
и используя равенства (7.12) и (7.13) придем к линейному дифференциальному уравнению первого порядка
с начальным условием
Пример 8. Найти решение уравнения
Решение. Вводим новую функцию
и находим её производную
затем дифференцируем исходное уравнение и подставляем новую функцию в полученное уравнение
Поделив результат на
и решаем его
Используя начальное условие определяем значение постоянной
Используя это значение находим
Ответ:
Нетрудно проверить что полученная функция удовлетворяет заданному уравнению, действительно, подставив найденное решение в исходное уравнение, найдём
=
Решение уравнений Вольтерра второго рода с помощью ряда Неймана Будем искать решение уравнения
в виде ряда по степеням параметра
Подставив ряд (8.2) в уравнение (8.1)
и приравнивая коэффициенты при одинаковых степенях
Докажем сходимость ряда (8.2) при найденных выражениях его коэффициентов (8.3) при следующих ограничениях
в квадрате Для выполнения условий (8.4) достаточно чтобы функция f(x) и ядро K(x,t) в рассматриваемой области были непрерывными. Для ядра K(x,t) можно условие ослабить, потребовав только его регулярность.Оценим коэффициенты ряда (8.2) по модулю в этой области
……………………………….
Построим ряд с полученными оценками коэффициентов ряда (8.2)
и положив в нём
Числовой ряд (8.5) сходится по признаку Даламбера
Ряд (8.5) по построению является мажорирующим для ряда (8.2), следовательно ряд (8.2) по критерию Вейерштрасса сходится равномерно и абсолютно.
Пример 9. Решить уравнение
Решение. Найдём коэффициенты ряда (8.2)
Подставив вычисленные коэффициенты в ряд (8.2) при
Ответ:
Итерированные ядра и резольвента
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 990; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.96.108 (0.006 с.) |


 . (7.1)
. (7.1) ,
,  . (7.2)
. (7.2)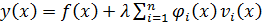 . (7.3)
. (7.3)

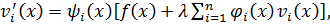
 (7.4) с начальными условиями
(7.4) с начальными условиями  .
. ,
,
 из данного уравнения найдём начальное условие
из данного уравнения найдём начальное условие  для дифференциального уравнения
для дифференциального уравнения ,
, .
.
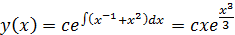 .
.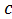 при
при  из общего решения не удается. Тогда воспользуемся значением при
из общего решения не удается. Тогда воспользуемся значением при  производной
производной  и продифференцировав общее решение
и продифференцировав общее решение ,
, .
.



 (7.5)
(7.5) , будем считать выполненным.
, будем считать выполненным.
 (7.6)
(7.6)
 . (7.7)
. (7.7)

 . (7.8)
. (7.8) из соотношения (7.7) и подставив в (7.8), получим систему линейных дифференциальных уравнений для определения функций
из соотношения (7.7) и подставив в (7.8), получим систему линейных дифференциальных уравнений для определения функций 
 , (7.9)
, (7.9)


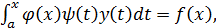 (7.11)
(7.11) (7.12)
(7.12) . (7,13)
. (7,13)
 (7.14)
(7.14) .
.

 ,
,
 , получим линейное дифференциальное уравнение
, получим линейное дифференциальное уравнение

 , следовательно
, следовательно и
и  .
.
 .
.

 (8.1)
(8.1)
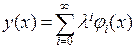 . (8.2)
. (8.2)
 слева и справа в полученном равенстве (так как ряды слева и справа от равенства равны только в этом случае) найдем
слева и справа в полученном равенстве (так как ряды слева и справа от равенства равны только в этом случае) найдем

 …,
…,  … (8.3)
… (8.3)
 (8.4)
(8.4)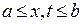 .
.
 ,
, ………………………………….…,
………………………………….…,
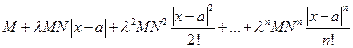
 , где
, где  любое, получим числовой ряд
любое, получим числовой ряд (8.5)
(8.5) .
.
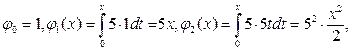
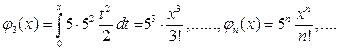 .
. найдём
найдём




