
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приведение уравнения второго порядка к каноническому виду.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение 11.9. Линия, определяемая общим уравнением второго порядка называется алгебраической линией второго порядка. Для квадратичной формы Для того, чтобы перейти к новой системе координат, в которой уравнение линии будет иметь канонический вид, необходимо провести два преобразования: 1) поворот координатных осей на такой угол, чтобы их направление совпало с направлением осей симметрии кривой (если она имеет две оси); 2) параллельный перенос, при котором начало координат совмещается с центром симметрии кривой (если он существует). Замечание. Для параболы новые оси координат должны располагаться параллельно и перпендикулярно директрисе, а начало координат – совпасть с вершиной параболы. Поскольку в канонических уравнениях кривых второго порядка отсутствуют произведения переменных, необходимо перейти к координатной системе, определяемой базисом из ортонормированных собственных векторов матрицы А. В этом базисе уравнение (11.5) примет вид: Зададим последующий параллельный перенос формулами: Рассмотрим возможные геометрические образы, определяемые этим уравнением в зависимости от знаков λ 1, λ 2 и 1) если собственные числа матрицы А λ 1 и λ 2 и (случаи 2) если λ 1 и λ 2 имеют разные знаки, уравнение (11.7) является каноническим уравнением гиперболы: В случае, когда одно из собственных чисел матрицы А равно 0, уравнение (11.5) в результате двух преобразований координат можно привести к виду: являющимся каноническим уравнением параболы.
Пример. Приведем к каноническому виду уравнение второго порядка 3 x ² + 10 xy +3 y ² - 2 x – 14 y – 13 = 0. Матрица квадратичной формы 3 x ² + 10 xy + 3 y ² имеет вид: Найдем ее собственные числа и собственные векторы. Составим характеристическое уравнение: e 2 = { Преобразуем полученное уравнение: 16. Определение 11.1. Кривыми второго порядка на плоскости называются линии пересечения кругового конуса с плоскостями, не проходящими через его вершину.
Если такая плоскость пересекает все образующие одной полости конуса, то в сечении получается эллипс, при пересечении образующих обеих полостей – гипербола, а если секущая плоскость параллельна какой-либо образующей, то сечением конуса является парабола.
Замечание. Все кривые второго порядка задаются уравнениями второй степени от двух переменных.
Эллипс.
Определение 11.2. Эллипсом называется множество точек плоскости, для которых сумма расстояний до двух фиксированных точек F 1 и F 2 этой плоскости, называемых фокусами, есть величина постоянная.
Замечание. При совпадении точек F 1 и F 2 эллипс превращается в окружность. Выведем уравнение эллипса, выбрав декартову систему
r1 r2 координат – с серединой отрезка F 1 F 2. Пусть длина этого отрезка равна 2 с, тогда в выбранной системе координат F1 O F2 x F 1(- c, 0), F 2(c, 0). Пусть точка М(х, у) лежит на эллипсе, и сумма расстояний от нее до F 1 и F 2 равна 2 а. Тогда r 1 + r 2 = 2 a, но поэтому
Определение 11.3. Эксцентриситетом эллипса называется величина е=с/а (11.2)
Определение 11.4. Директрисой Di эллипса, отвечающей фокусу Fi, называется прямая, расположенная в одной полуплоскости с Fi относительно оси Оу перпендикулярно оси Ох на расстоянии а/е от начала координат.
Замечание. При ином выборе системы координат эллипс может задаваться не каноническим уравнением (11.1), а уравнением второй степени другого вида.
Свойства эллипса: 1) Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром – начало координат. Поскольку длины отрезков, образованных пересечением эллипса с главными осями, равны 2 а и 2 b (2 a >2 b), то главная ось, проходящая через фокусы, называется большой осью эллипса, а вторая главная ось – малой осью. 2) Весь эллипс содержится внутри прямоугольника 3) Эксцентриситет эллипса e < 1. Действительно, 4) Директрисы эллипса расположены вне эллипса (так как расстояние от центра эллипса до директрисы равно а/е, а е <1, следовательно, а/е>a, а весь эллипс лежит в прямоугольнике 5) Отношение расстояния ri от точки эллипса до фокуса Fi к расстоянию di от этой точки до отвечающей фокусу директрисы равно эксцентриситету эллипса. Доказательство. Расстояния от точки М(х, у) до фокусов эллипса можно представить так:
Гипербола. Определение 11.5. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний до двух фиксированных точек F 1 и F 2 этой плоскости, называемых фокусами, есть величина постоянная.
Выведем каноническое уравнение гиперболы по аналогии с выводом уравнения эллипса, пользуясь теми же обозначениями. | r1 - r2| = 2 a, откуда
Определение 11.6. Эксцентриситетом гиперболы называется величина е = с / а.
Определение 11.7. Директрисой Di гиперболы, отвечающей фокусу Fi, называется прямая, расположенная в одной полуплоскости с Fi относительно оси Оу перпендикулярно оси Ох на расстоянии а / е от начала координат.
Свойства гиперболы: 1) Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ох для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах – ось Оу). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси. 2) Ветви гиперболы имеют две асимптоты, определяемые уравнениями 3) Наряду с гиперболой (11.3) можно рассмотреть так называемую сопряженную гиперболу, определяемую каноническим уравнением для которой меняются местами действительная и мнимая ось с сохранением тех же асимптот. 4) Эксцентриситет гиперболы e > 1. 5) Отношение расстояния ri от точки гиперболы до фокуса Fi к расстоянию di от этой точки до отвечающей фокусу директрисы равно эксцентриситету гиперболы. Доказательство можно провести так же, как и для эллипса.
Парабола.
Определение 11.8. Параболой называется множество точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно расстоянию до некоторой фиксированной прямой. Точка F называется фокусом параболы, а прямая – ее директрисой.
систему координат так, чтобы ее началом была середина
r су, а координатные оси располагались параллельно и перпендикулярно директрисе. Пусть длина отрезка FD D O F x равна р. Тогда из равенства r = d следует, что называемому каноническим уравнением параболы. Величина р называется параметром параболы.
Свойства параболы: 1) Парабола имеет ось симметрии (ось параболы). Точка пересечения параболы с осью называется вершиной параболы. Если парабола задана каноническим уравнением, то ее осью является ось Ох, а вершиной – начало координат. 2) Вся парабола расположена в правой полуплоскости плоскости Оху.
Замечание. Используя свойства директрис эллипса и гиперболы и определение параболы, можно доказать следующее утверждение: Множество точек плоскости, для которых отношение е расстояния до некоторой фиксированной точки к расстоянию до некоторой прямой есть величина постоянная, представляет собой эллипс (при e <1), гиперболу (при e >1) или параболу (при е =1).
17. Определение 12.1. Поверхностью второго порядка называется множество точек трехмерного пространства, декартовы координаты которых удовлетворяют уравнению вида: уравнению второй степени от трех неизвестных, называемому общим уравнением поверхности второго порядка.
18. Конус. Поверхность, образованная прямыми линиями, проходящими через данную точку Р и пересекающими данную плоскую линию L (не проходящую через Р) называется конической поверхностью или конусом. При этом линия L называется направляющей конуса, точка Р – ее вершиной, а прямая, описывающая поверхность, называется образующей. Эллипсоид. Рассмотрим сечение поверхности с плоскостями, параллельными xOy. Уравнения таких плоскостей z=h, где h – любое число. Линия, получаемая в сечении, определяется двумя уравнениями: Если |h|>c, c>0, то Если |h|=c, т.е. h=±c, то . Линия пересечения вырождается в две точки (0;0;с) и (0;0;-с). Плоскости z=c и z=–c касаются поверхности. Если |h|<c, то уравнения можно переписать в виде: Линия пересечения есть эллипс с полуосями. Эллипсоид – замкнутая овальная поверхность, где a,b,с – полуоси. Если все они различны, то эллипсоид называется трехосным. Если какие-либо две полуоси равны, то тело называется эллипсоид вращения, если a=b=c, то тело называется сферой x2+y2+z2=R2 19. Однополостный гиперболоид Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени. К ним относится однополосный гиперболоид. Однополосный гиперболоид. Однополосным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
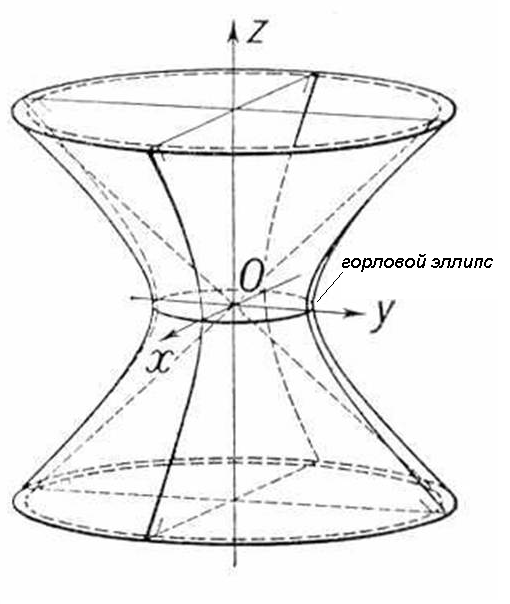
Из уравнения (1) вытекает, что координатные плоскости являются плоскостями симметрии, а начало координат — центром симметрии однополостного гиперболоида. Уравнение (1) называется каноническим уравнением однополосного гиперболоида. Если однополостный гиперболоид задан своим каноническим уравнением (1) то оси Ох, Оу и Oz называются его главными осями. Установим вид поверхности (1). Для этого рассмотрим сечение ее координатными плоскостями Oxy (y=0) и Oyx (x=0). Получаем соответственно уравнения
из которых следует, что в сечениях получаются гиперболы.
из которых следует, что плоскость z=h пересекает гиперболоид по эллипсу с полуосями достигающими своих наименьших значений при h=0, т.е. в сечении данного гиперболоида координатной осью Oxy получается самый маленький эллипс с полуосями a*=a и b*=b. При бесконечном возрастании
Таким образом, рассмотренные сечения позволяют изобразить однополосный гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления (по обе стороны) от плоскости Oxy. Величины a, b, c называются полуосями однополосного гиперболоида. Исследование поверхности методом параллельных сечений. Суть метода заключается в выяснении формы линий пересечения поверхности с плоскостями, параллельными координатным плоскостям. Рассмотрим линии пересечения с плоскостями, параллельными плоскости OXY. Все уравнения линий пересечений будут получаться из уравнения плоскости, в котором z будет заменена на некоторое число, равное расстоянию от пересекающей плоскости до плоскости OXY. Для более наглядного представления, я изобразил все полученные кривые в виде проекций на плоскость OXY. Изображения кривых представлены выше. Величины a, b, c называются полуосями однополосного гиперболоида. Если a=b,то гиперболоид может быть получен вращением гиперболы с полуосями а и с вокруг мнимой оси 2с.
Двуполостным гиперболоидом называется поверхность, заданная относительно специально выбранной системы координат уравнением x2/a2+y2/b2-z2/c2=-1 (1). Если точка (x, y, z) принадлежит двуполостному гиперболоиду (1), то на этой поверхности лежит точка с координатами (±x, ±y, ±z) при любом наборе знаков, следовательно начало координат является центром двуполостного гиперболоида, координатные оси — осями симметрии, координатные плоскости — плоскостями симметрии. Вершинами двуполостного гиперболоида называются точки пересечения поверхности с осью oz (0, 0, ±c). http://uchim.org/algebra-i-geometrija/dvupolostnyj-giperboloid - uchim.org Пусть в (1) a=b, тогда двуполостный гиперболоид получается вращением гиперболы x2/a2-z2/c2=-1 или z2/c2-x2/a2=1, у которой ось oz является её вещественной осью, а ox мнимой. Вращение гиперболы осуществляется вокруг оси oz. В этом случае двуполостный гиперболоид называется двуполостным гиперболоидом вращения.
20. Эллиптический параболоид
Так как в (10) присутствуют квадраты переменных Пересекая поверхность (10) плоскостями
с полуосями
При изменении Пересекая поверхность (10) плоскостями
со смещенной вершиной в точке При Точка
Рис. 46 Гиперболический параболоид
По виду уравнения (11) заключаем, что данная поверхность симметрична относительно плоскостей
причем при При сечении поверхности (11) плоскостями
Поверхность (11) изображена на рис.47.
Рис.47 21. Определение. Действительные числа – это рациональные и иррациональные числа. Так как любое рациональное число может быть записано в виде конечной десятичной дроби или бесконечной периодической дроби, а иррациональные числа представляются бесконечными непериодическими десятичными дробями, то озвученное определение действительных чисел можно переформулировать следующим образом. Определение. Действительные числа – это числа, которые могут быть записаны в виде конечной или бесконечной (периодической или непериодической) десятичной дроби.
Множество вещественных чисел разбивается на два множества — Q рациональных и`Q (I) иррациональных чисел.
Определение 1: Рациональным называется число, которое можно представить в виде p / q, где р и q — целые числа, причем q ¹0.
Определение 2: Иррациональным называется всякое вещественное число, которое не является рациональным.
Всякое рациональное число p / q является либо целым, либо его можно представить в виде конечной или периодической бесконечной десятичной дроби. Всякое иррациональное число представляется непериодической бесконечной десятичной дробью.
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 895; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.135.201 (0.009 с.) |

 , (11.5)
, (11.5) можно задать матрицу
можно задать матрицу . (11.6)
. (11.6)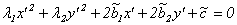 (в предположении, что λ 1,2 не равны 0).
(в предположении, что λ 1,2 не равны 0). . Получим в новой координатной системе уравнение
. Получим в новой координатной системе уравнение . (11.7)
. (11.7) :
: , где
, где 
 и
и  или
или  , в зависимости от знака
, в зависимости от знака  , (11.8)
, (11.8) .
. Для координат собственного вектора е 1, соответствующегоλ1, получим с учетом нормировки:
Для координат собственного вектора е 1, соответствующегоλ1, получим с учетом нормировки: , откуда e 1 = {
, откуда e 1 = {  }. Аналогично найдем е 2:
}. Аналогично найдем е 2:  ,
,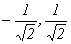 }. Составим матрицу перехода к новому базису, столбцами которой будут координаты собственных векторов:
}. Составим матрицу перехода к новому базису, столбцами которой будут координаты собственных векторов:  . Тогда
. Тогда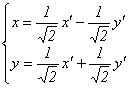 . Подставив эти выражения в исходное уравнение, получим его вид в новой системе координат:
. Подставив эти выражения в исходное уравнение, получим его вид в новой системе координат:  Заметим, что коэффициентами при x ² и y ² являются λ 1 и λ 2.
Заметим, что коэффициентами при x ² и y ² являются λ 1 и λ 2.
 Зададим параллельный перенос формулами:
Зададим параллельный перенос формулами:  . Получим уравнение:
. Получим уравнение:  , а после деления на 8:
, а после деления на 8: - каноническое уравнение гиперболы.
- каноническое уравнение гиперболы.



 у М(х,у) координат так, чтобы ось Ох совпала с прямой F 1 F 2, начало
у М(х,у) координат так, чтобы ось Ох совпала с прямой F 1 F 2, начало ,
, Введя обозначение b ² = a ²- c ² и проведя несложные алгебраические преобразования, получим каноническое уравнение эллипса:
Введя обозначение b ² = a ²- c ² и проведя несложные алгебраические преобразования, получим каноническое уравнение эллипса:  (11.1)
(11.1)

 Составим уравнения директрис:
Составим уравнения директрис: (D 1),
(D 1),  (D 2). Тогда
(D 2). Тогда 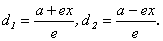 Отсюда ri / di = e, что и требовалось доказать.
Отсюда ri / di = e, что и требовалось доказать. Если обозначить b ² = c ² - a ², отсюда можно получить
Если обозначить b ² = c ² - a ², отсюда можно получить - каноническое уравнение гиперболы. (11.3)
- каноническое уравнение гиперболы. (11.3) и
и  .
. , (11.3`)
, (11.3`)
 у Для вывода уравнения параболы выберем декартову
у Для вывода уравнения параболы выберем декартову

 d M(x,y) перпендикуляра FD, опущенного из фокуса на директри-
d M(x,y) перпендикуляра FD, опущенного из фокуса на директри- поскольку
поскольку Алгебраическими преобразованиями это уравнение можно привести к виду: y ² = 2 px, (11.4)
Алгебраическими преобразованиями это уравнение можно привести к виду: y ² = 2 px, (11.4) - (12.1)
- (12.1) , целиком принадлежит этой поверхности.
Теорема (об уравнении поверхности вращения).
Если в некоторой декартовой прямоугольной системе координат поверхность S задана уравнением
F(x2+y2,z)=0, то S — поверхность вращения вокруг оси OZ.
, целиком принадлежит этой поверхности.
Теорема (об уравнении поверхности вращения).
Если в некоторой декартовой прямоугольной системе координат поверхность S задана уравнением
F(x2+y2,z)=0, то S — поверхность вращения вокруг оси OZ.



 - уравнение конуса
- уравнение конуса

 точек пересечения поверхности с плоскостями z=h нет.
точек пересечения поверхности с плоскостями z=h нет.

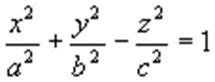 (1)
(1) 
 и
и 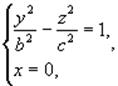

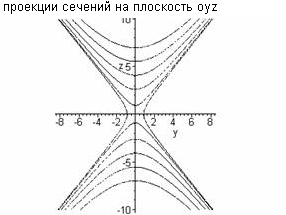 Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями
Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями или
или 
 и
и  ,
, величины a* и b* возрастают бесконечно.
величины a* и b* возрастают бесконечно.


 . (10)
. (10)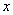 и
и  , то данная поверхность симметрична относительно координатных плоскостей
, то данная поверхность симметрична относительно координатных плоскостей  ,
,  . Далее, так как мы считаем
. Далее, так как мы считаем  , то поверхность (10) расположена в полупространстве
, то поверхность (10) расположена в полупространстве  .
. , в сечении будем получать эллипсы.
, в сечении будем получать эллипсы.
 ,
,  .
. от нуля до
от нуля до  данные эллипсы описывают нашу поверхность (10).
данные эллипсы описывают нашу поверхность (10). (или
(или  ), мы получим в сечении параболы
), мы получим в сечении параболы

 .
. поверхность (10) будет поверхностью вращения, получающейся от вращения параболы
поверхность (10) будет поверхностью вращения, получающейся от вращения параболы 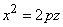 около оси
около оси  . В этом случае поверхность (10) называют параболоидом вращения.
. В этом случае поверхность (10) называют параболоидом вращения. лежит на поверхности (10) и называется вершиной эллиптического параболоида. Эллиптический параболоид изображен на рис. 46.
лежит на поверхности (10) и называется вершиной эллиптического параболоида. Эллиптический параболоид изображен на рис. 46.

 , мы будем получать в сечении гиперболы
, мы будем получать в сечении гиперболы ,
, действительная ось симметрии гиперболы будет параллельной оси
действительная ось симметрии гиперболы будет параллельной оси  , а при
, а при  - оси
- оси  . При
. При  в сечении будут две пересекающиеся прямые.
в сечении будут две пересекающиеся прямые. ,
,  .
.



