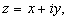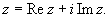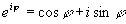Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Следствие 2 (фальшивое разложение определителяСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Сумма произведений всех элементов некоторой строки (столбца) матрицы А на алгебраические дополнения соответствующих элементов любой другой строки (столбца) равна нулю. Доказательство. Рассмотрим сумму произведений всех элементов произвольной k-ой строки матрицы А на алгебраические дополнения соответствующих элементов любой другой, скажем, i-ой строки матрицы А. Пусть A′ – матрица, у которой все строки, кроме i-ой, такие же, как у матрицы А, а элементами i-ой строки матрицы A′ являются соответствующие элементы k-ой строки матрицы А. Тогда у матрицы A′ две одинаковые строки и, следовательно, по свойству матрицы об одинаковых строках имеем, что |A′| = 0. С другой стороны, по следствию 1 определитель |A′| равен сумме произведений всех элементов i-ой строки матрицы A′ на их алгебраические дополнения. Заметим, что алгебраические дополнения элементов i-ой строки матрицы A′ совпадают с алгебраическими дополнениями соответствующих элементов i-ой строки матрицы А. Но элементами i-ой строки матрицы A′ являются соответствующие элементы k-ой строки матрицы А. Таким образом, сумма произведений всех элементов i-ой строки матрицы A′ на их алгебраические дополнения с одной стороны равна нулю, а с другой стороны равна сумме произведений всех элементов k-ой строки матрицы А на алгебраические дополнения соответствующих элементов i-ой строки матрицы А. 4. ПРАВИЛО КРАМЕРА Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,
называется определителем системы. Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов
Тогда можно доказать следующий результат. Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A11 элемента a11, 2-ое уравнение – на A21 и 3-е – на A31:
Сложим эти уравнения:
Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца
Далее рассмотрим коэффициенты при x2:
Аналогично можно показать, что и Наконец несложно заметить, что Таким образом, получаем равенство: Следовательно, Аналогично выводятся равенства Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна. Примеры. Решить систему уравнений Итак, х =1, у =2, z =3.
Система имеет единственное решение, если Δ ≠ 0.
6. Комплексным числом z называется упорядоченная пара действительных чисел x и y. Алгебраическая форма записи комплексного числа
Число Комплексное число z = x + iy естественно изображать в виде точки на плоскости с декартовыми координатами (x, y).
Если x и y - декартовы координаты точки плоскости, то, перейдя на плоскости к полярным координатам (r, j) и воспользовавшись связью При решении задач для вычисления аргумента удобно пользовааться схемой, приведенной ниже: Справедливы соотношения: Используя формулу Эйлера Понятие комплексного числа Определение комплексного числа: комплексное число - это упорядоченная пара действительных чисел. Если каждому действительному числу соответствует точка числовой прямой, то каждому комплексному числу соответствует точка координатной плоскости. Пример комплексного числа: (2; 4), это упорядоченная пара действительных чисел. Как понимать "упорядоченная"? В нашем примере (2; 4) на первом месте стоит 2, а на втором стоит 4. Если поменять местами эти числа, вот так (4; 2), то мы получаем другое число, которое не равно числу (2; 4). Комплексное число (0; 0) называют комплексным нулём.
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 2310; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.26.8 (0.007 с.) |

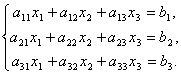


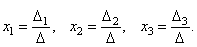
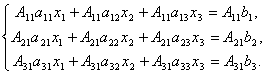
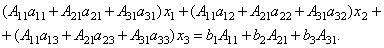
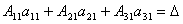 .
.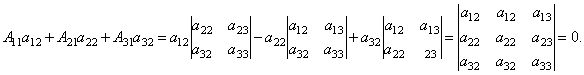
 .
.
 .
.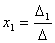 .
.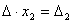 и
и 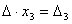 , откуда и следует утверждение теоремы.
, откуда и следует утверждение теоремы.
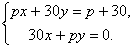
 . Поэтому
. Поэтому 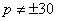 .
.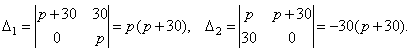
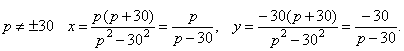
 которая не имеет решений.
которая не имеет решений. и, следовательно, имеет бесконечное множество решений x=y, yÎR.
и, следовательно, имеет бесконечное множество решений x=y, yÎR. 
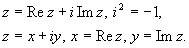
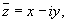
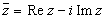 , где
, где