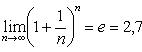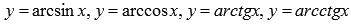Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль вещественного числа и его свойстваСодержание книги
Поиск на нашем сайте
Определение. Модуль вещественного числа
Свойства модуля 1.
2. 3. Понятие последовательности
Если функция определена на множестве натуральных чисел N, то такая функция называется бесконечной числовой последовательностью. Обычно числовые последовательность обозначают как(Xn), где n принадлежит множеству натуральных чисел N. Числовая последовательность может быть задана формулой. Например, Xn=1/(2*n). Таким образом мы ставим в соответствие каждому натуральному числу n некоторый определенный элемент последовательности (Xn). Если теперь последовательно брать n равными 1,2,3, …., мы получим последовательность (Xn): ½, ¼, 1/6, …, 1/(2*n), … Виды последовательности Последовательность может быть ограниченной или неограниченной, возрастающей или убывающей. Последовательность (Xn) называет ограниченной, если существуют два числа m и M такие, что для любого n принадлежащего множеству натуральных чисел, будет выполняться равенство m<=Xn Последовательность (Xn), не являющаяся ограниченной, называется неограниченной последовательностью. Последовательность (Xn) называется возрастающей, если для всех натуральных n выполняется следующее равенство X(n+1) > Xn. Другими словами, каждый член последовательности, начиная со второго, должен быть больше предыдущего члена. Последовательность (Xn) называется убывающей, если для всех натуральных n выполняется следующее равенство X(n+1) < Xn. Иначе говоря, каждый член последовательности, начиная со второго, должен быть меньше предыдущего члена. Пример последовательности Проверим, являются ли последовательности 1/n и (n-1)/n убывающими. Если последовательность убывающая, то X(n+1) < Xn. Следовательно X(n+1) – Xn < 0. 1/n: X(n+1) – Xn = 1/(n+1) – 1/n = -1/(n*(n+1)) < 0. Значит последовательность 1/n убывающая. (n-1)/n: X(n+1) – Xn =n/(n+1) - (n-1)/n = 1/(n*(n+1)) > 0. Значит последовательность (n-1)/n возрастающая.
Бесконечно малые последовательности Определение бесконечно малой последовательности Последовательность
Свойства бесконечно малых последовательностей
Примеры
23. Сходящиеся последовательности и их свойства Рассмотрим числовые последовательности. Последовательность (xn) действительных чисел называется сходящейся, если существует действительное число a и для произвольного ε > 0 существует натуральное число m такое, что для всех n > m справедливо неравенство | xn - a | < ε. При этом число a называют пределом последовательности (xn), что символически записывают
С помощью логических символов определение запишется следующим образом: числовая последовательность (xn) называется сходящейся, если
24. Определение. 1) Если xn+1 > xn для всех n, то последовательность возрастающая. 2)Если xn+1 ³ xn для всех n, то последовательность неубывающая. 3)Если xn+1 < xn для всех n, то последовательность убывающая. 4)Если xn+1 £ xn для всех n, то последовательность невозрастающая Все эти последовательности называются монотонными. Возрастающие и убывающие последовательности называются строго монотонными. Число e Последовательность
25. Основными элементарными функциями являются: постоянная функция (константа), корень n-ой степени, степенная функция, показательная, логарифмическая функция, тригонометрические и обратные тригонометрические функции.
26.
|
|||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1526; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.79.187 (0.01 с.) |

 — это само число
— это само число  , и противоположное число
, и противоположное число  , если
, если 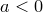 .
.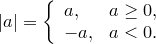
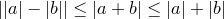 ,
,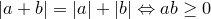 .
. .
. — это расстояние между точками
— это расстояние между точками 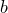 на числовой оси.
на числовой оси. называется бесконечно малой, если
называется бесконечно малой, если  , т.е.
, т.е.  .
. , то
, то  .
. – бесконечно малая, т.к.
– бесконечно малая, т.к. 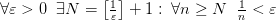 .
.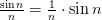 — бесконечно малая, т.к.
— бесконечно малая, т.к.  – ограниченная, а
– ограниченная, а  .
. – бесконечно малая, т.к.
– бесконечно малая, т.к.  — ограниченная, а
— ограниченная, а  – бесконечно малая при
– бесконечно малая при  , т.к.
, т.к. 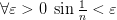 при
при  .
.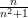 – бесконечно малая, т.к.
– бесконечно малая, т.к.  , которая является бесконечно малой.
, которая является бесконечно малой.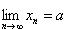 или xn → a при n → ∞.
или xn → a при n → ∞.





 , имеет конечный предел, называемый числом е:
, имеет конечный предел, называемый числом е: