Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Размерность линейного пространстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим произвольное вещественное пространство R. Определение 3.1. Линейное пространство R называется n-мерным, если в нем существует n линейно независимых элементов, а любые (n +1) элементов уже являются линейно зависимыми. При этом число n называется размерностью пространства R. Размерность пространства обозначают символом dim. Определение 3.2. Линейное пространство R называется бесконечномерным, если в нем существует любое число линейно независимых элементов. Теорема 3.3. Пусть R является линейным пространствам размерности n (dim R=n). Тогда любые n линейно независимых элементов этого пространства образуют его базис. Доказательство. Так как R является n -мерным пространством, то из определения 2.1 следует, что в нем существует совокупность из n линейно независимых элементов
Заметим, что λ 0≠0 т.к. в противном случае из равенства (3.1) следовала, что элементы
получим
(3.3) Из равенства (3.3) следует, что любой вектор из пространства R может быть разложен по элементам Теорема 3.4. Пусть линейное пространство R имеет базис, состоящий из n элементов. Тогда размерность R равна n (dim R=n). Доказательство. Пусть множество n элементов
(3.4) где a 11, a 12 ,..., a n+1,n вещественные числа. Пусть элементы
(3.5)
где
(3.7) Так как
(3.8) Подставляя (3.8) в (3.6), получим:
Как видно из уравнения (3.9)
Линейная зависимость векторов, теоремы о линейной зависимости. Определение 1. Система векторов
Система векторов Выражение стоящее в левой части рав-ва (1) наз-ют линейной комбинацией векторов Определение 2. Система векторов является линейно зависимой, если существует линейная комбинация этих векторов с неравными 0 числами, которая тождественно равна. Теорема 1. Если система векторов Доказательствово. Пусть
Теорема 2. Если к системе линейно зависимых векторов Доказательство. Т.К. система векторов
Есть
Следовательно система линейно зависима. Следствие. Если к линейно зависимой системе добавить любое кол-во векторов, то полученная система будет линейно зависима. Теорема о линейной зависимости двух векторов Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны. Доказательство.
Теорема. Три вектора линейно зависимы тогда и только тогда, когда они компланарны Доказательство.
Для Теорема. В трехмерном пространстве любые 4 вектора линейно зависимы. Доказательство.
Вектор в системе координат Базис-максимальная упорядоченная система линейно независимых векторов.
На плоскости 2 любых неколлинеарных вектора образуют базис. ДПБ-базис, состоящий из ортогональных еденичных векторов.
Операции над векторами в координатной форме.
направляющие косинусы
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 593; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.138.33 (0.011 с.) |

 . Пусть x - любой элемент из R. Тогда согласно определению 3.1
. Пусть x - любой элемент из R. Тогда согласно определению 3.1  линейно зависимы, т.е. существуют числа
линейно зависимы, т.е. существуют числа  (не все равные нулю) такие, что справедливо равенство
(не все равные нулю) такие, что справедливо равенство

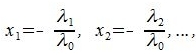
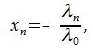

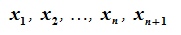 этого пространства линейно зависимы. Разложив эти элементы по базису, получим:
этого пространства линейно зависимы. Разложив эти элементы по базису, получим:
 линейно независимы. Перепишем (3.4) в матричном виде:
линейно независимы. Перепишем (3.4) в матричном виде: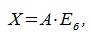


 ,
,  n×n-матрицы(элементы
n×n-матрицы(элементы  здесь являются вектор-строками),
здесь являются вектор-строками),
 получим:
получим:


 можно представить линейной комбинацией векторов
можно представить линейной комбинацией векторов  называется линейно зависимой, если сущ. числа
называется линейно зависимой, если сущ. числа  не все равные 0, такие что
не все равные 0, такие что  (1)
(1) , тогда
, тогда 


 , то вновь полученная система будет линейно зависима.
, то вновь полученная система будет линейно зависима. (3)
(3) (4)
(4) ,
,  0 -не все равны нулю
0 -не все равны нулю


 -коллинеарны
-коллинеарны




 и
и  пл-ть
пл-ть  , что
, что  (или //) и
(или //) и 

 либо
либо  , либо // ей
, либо // ей 


 -угол между
-угол между 




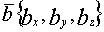
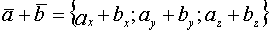



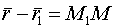







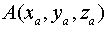 -нач.точка
-нач.точка 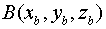 -кон.точка
-кон.точка